El método de resolución que se indica en el papiro Rhind fue enseñado hasta principios del siglo XX. En un documento conservado del segundo siglo antes de nuestra era se considera el siguiente problema:
Para 3 gavillas de una buena cosecha, 2 de una mediana cosecha y una de una mala cosecha se reciben 39 Tou. Para 2 gavillas de una buena cosecha, 3 de una mediana cosecha y una de una mala cosecha se reciben 34 Tou. Para 1 gavilla de una buena cosecha, 2 de una mediana cosecha y 3 de una mala cosecha se reciben 26 Tou. ¿Cuánto se recibe para cada gavilla de una buena, de una mediana y de una mala cosecha?
Hoy diríamos que en este problema se trata de plantear un sistema de ecuaciones lineales. El método que se indica en el documento chino es el que hoy conocemos como algoritmo de Gauss; no obstante Gauss vivió dos milenios después de Fang Cheng, el autor del documento. Pero la historia rara vez hace justicia al atribuir los descubrimientos y tiende a dar a quien ya tiene.
Problemas como los que se han presentado sugirieron la invención de variables, una hazaña que tardó varios siglos y tuvo muchos altibajos. Los matemáticos árabes, en particular después de la obra de Al-Juarismi, introdujeron propiamente el álgebra elemental como la conocemos hoy día, comprendiendo el concepto de ecuación algebraica y de polinomios, la solución numérica de ecuaciones y la construcción geométrica de soluciones.
Al-Juarismi nació alrededor de 790, vivió y trabajó en Bagdad y murió, aproximadamente, de sesenta años. Su libro contenía una clasificación de ecuaciones cuadráticas y cómo resolverlas de manera geométrica. Los tipos de ecuaciones que trataba Al-Juarismi se leen en la notación moderna como:
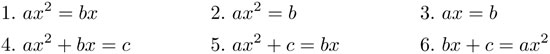
Hay que notar que sólo consideraba soluciones y coeficientes positivos. Luego, dividió estas ecuaciones entre el coeficiente a, con el fin de obtener "formas normales". Para cada uno de estos tipos deriva una fórmula de solución usando ejemplos y argumentaciones geométricas. Por ejemplo, la argumentación geométrica para resolver la ecuación x2 + q = px se basa en la figura 4.30.
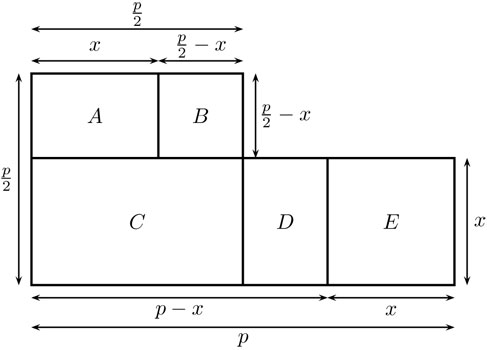
En la figura se ve que el rectángulo C tiene la mitad de ancho que CDE juntos. Por ello, C = D + E si con los mismos símbolos se denotan las áreas. Además C + D = (p - x) x = q, según la ecuación que se quiere resolver, que es x2 + q = px. Finalmente, se observa que A y D son congruentes. Entonces, podemos calcular:
es decir,
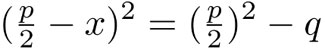
lo que ahora se puede resolver fácilmente pues:
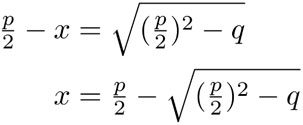
De esta manera, se comprende mucho mejor el título de la obra que se traduce como "Compendio de cálculo por el método de completado y balanceado", ya que el argumento anterior muestra cómo se balancean los términos para lograr expresar la incógnita en un cuadrado.
Después de Al-Juarismi hubo muchos otros matemáticos árabes, de los cuales destacaron, principalmente, el matemático persa Al-Karaji, quien usó los monomios x, x2, x3…y 
,... sin representación geométrica, y después Omar Khayyam, quien clasificó y resolvió la ecuación cúbica al usar intersecciones de secciones cónicas.
Los conocimientos de los árabes se difundieron poco a poco en Europa, durante los siglos XII, XIII y XIV; se sabe también que a finales del siglo XV las principales obras de griegos como Euclides, Apolonio, Diofanto, Herón y Arquímedes, entre otros, ya se conocían. Fue precisamente en esta época cuando Tartaglia, Cardano y Ferrer desarrollaron la solución general de la ecuación algebraica de tercer y cuarto grado que detallamos en la sección 4.11.
Los ejemplos mostrados en esta sección ponen de manifiesto que el álgebra básica se desarrolló en diferentes regiones del planeta, de manera independiente.
Lo que sigue es una de las historias más asombrosas y que sólo ocurrió una vez, en Europa.
