Siempre que medimos algo hay que indicar la unidad en la que se mide. Decir que el objeto "pesa 4" carece de sentido cuando no se aclara si se trata de kilogramos, gramos, toneladas, libras u onzas. Las medidas utilizadas han cambiado durante la historia y buena parte de las que usamos en la actualidad se establecieron en Francia, después de la Revolución y a principios del siglo XIX. El metro, por ejemplo, se estableció como la diezmilésima parte de la distancia del Ecuador al Polo Norte. Lo importante es que cualquier medida fija puede servir como unidad.
Si tenemos un segmento de 1.2cm de longitud y otro de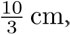 
podemos usar un tercero como unidad, de 
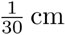de longitud, y medir los dos primeros: el segmento de 1.2cm de largo es 36 veces la unidad, mientras que el segmento 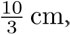de es 100 veces la unidad. Por lo tanto, encontramos una unidad de medida para expresar la longitud de ambos segmentos como un múltiplo entero de esta unidad. Estas ideas se atribuyen a los pitagóricos, la escuela que fundó Pitágoras en el siglo V a. C. Dos segmentos cualesquiera que se pueden medir con una misma unidad los llamaron conmensurables. Los pitagóricos partieron tácitamente de la suposición de que cada dos segmentos son conmensurables.
Para los pitagóricos, los números enteros eran centrales pues, con ellos, se expresaba la naturaleza, por ejemplo, en las relaciones de las notas con la música. Grande fue su asombro al descubrir que hay segmentos que no se pueden medir con una sola unidad; tal es el caso del lado de un cuadrado y su diagonal, que no son conmensurables. La leyenda cuenta que Hippasus, el pitagórico que hizo este descubrimiento, fue echado por la borda del barco cuando comunicó su hallazgo.
En la sección 1.4 expusimos una demostración de este hecho: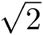 
no es racional y, de ahí, sigue la inconmensurabilidad del lado y la diagonal: si hubiera una unidad u para expresar la longitud del lado de un cuadrado l = mu —donde m es un entero— y también la diagonal 
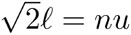— con n, un entero—, entonces 
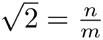es racional, lo cual es una contradicción pues sabemos que 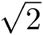no es racional.
La existencia de segmentos inconmensurables es, tal vez, la primera ocurrencia en las matemáticas de una demostración de algo que no existe: no existe y nunca existirá una unidad para medir el lado y la diagonal de un cuadrado con números enteros. En este tema se tratarán varios hallazgos matemáticos y cada uno de ellos afirmará que algo no existe de manera determinante. A la vez, cada uno tiene que ver con una pregunta importante y una teoría completa que hubo que desarrollar para poder llegar a la conclusión de la no-existencia.
