"Reparte 10 sacos de cebada entre 10 hombres de modo que la diferencia entre la parte de cada hombre y la de sus vecinos sea 1/8 de saco." Este problema es uno más que se plantea en el papiro de Rhind.
Alrededor del año 1700 a.C., Ahmes —un escribano egipcio— elaboró un texto en el que se recopilaban ochenta problemas matemáticos, todos ellos relacionados con situaciones concretas de la vida cotidiana, como la medición de la Tierra o la repartición de bienes. Este papiro fue encontrado en 1858 en Luxor, Egipto, por un anticuario escocés que se llamaba Henry Rhind y en 1863, luego de ser entregado al Museo Británico, se le llamó el papiro de Rhind.
Hace miles de años, en las civilizaciones babilonia y egipcia, las matemáticas estaban orientadas, fundamentalmente, a resolver problemas prácticos. No fue sino hasta varios siglos más tarde cuando los matemáticos griegos dieron a las matemáticas un carácter completamente distinto. Para ellos, no bastaba que el conocimiento matemático resolviera problemas concretos que se comprobaran a través de la experiencia, sino que buscaban la generalización de los resultados y su deducción, a partir de otros. Por consiguiente, organizaron las matemáticas como un sistema deductivo donde el único método válido para obtener resultados era el método axiomático.
El ejemplo más importante en las matemáticas griegas es la obra Los elementos de Euclides, quien vivió en Alejandría hacia el año 300 a.C. En este libro —compuesto por trece capítulos— Euclides recopiló y organizó en forma deductiva gran parte de la geometría y aritmética conocida en su época.
Los griegos hicieron de las matemáticas una ciencia teórica y deductiva en la que, para justificar una afirmación, no es suficiente probarla al comprobar que se cumple en casos particulares —aunque sean muchísimos—, sino que es necesario establecerla como un teorema.
Un teorema es una afirmación que se demuestra por medio de la argumentación lógica y de forma deductiva a partir de otros teoremas que, a la vez, ya han sido demostrados. Como las demostraciones no pueden ser indefinidas, se parte de ciertos principios tan claros y evidentes que se pueden asumir sin necesidad de demostrarlos: las definiciones, los postulados y los axiomas. El método axiomático consiste, a grandes rasgos, en lo anterior y con ello los griegos dieron un gran paso hacia la fundamentación de las matemáticas.
Un filósofo griego que no podemos dejar de mencionar aquí es Aristóteles, que nació en el 384 a.C. en Macedonia y que propuso el razonamiento deductivo a partir de silogismos, como el que se muestra a continuación:
• Todos los hombres son mortales,
• Sócrates es hombre,
por lo tanto,
• Sócrates es mortal.
El nombre de Aristóteles estará siempre ligado al de su maestro, Platón, quien a la vez era discípulo de Sócrates y estudioso y admirador de Pitágoras. Es decir, los nombres de los filósofos, matemáticos y físicos griegos están entrelazados en la búsqueda de una estructura que le diera rigor a las formas de pensamiento matemático.
Debemos a Euclides el método axiomático, lo que constituye un gran paso en la historia de las matemáticas, pues introduce la manera moderna o actual de hacerlas.
En un principio, el método axiomático era intuitivo, es decir, los axiomas y los postulados se establecían como evidentes —y por lo tanto no era necesario demostrarlos—, porque así se veían en la realidad, y las deducciones que se hacían a partir de ellos eran, también, bastante intuitivas.
Poco a poco, y con el paso de los siglos, los sistemas axiomáticos se fueron haciendo más abstractos y, entonces, lo importante no era ya que los axiomas y los teoremas se adecuaran a la realidad, sino que formaran un cuerpo de afirmaciones consistente: libre de contradicciones. En otras palabras, que mediante los axiomas no pudieran demostrarse a la vez una afirmación y su negación, por ejemplo: "a es igual a b" y, al mismo tiempo, que también se demostrara que "a no es igual a b".
¿Cómo saber que un sistema de axiomas no lleva a contradicciones, es decir, cómo saber que, a partir de los axiomas y de las reglas lógicas que usamos para hacer deducciones, no se pueden deducir un teorema y su negación? Aunque a primera vista pueda parecer increíble, esta pregunta ha ocupado a varios filósofos y matemáticos a lo largo de los siglos.
La sistematización del pensamiento matemático fue dando lugar a preguntas muy importantes —complejas y entrelazadas entre sí—, que hoy día siguen vigentes, acerca de los fundamentos de las matemáticas:
• ¿Las matemáticas se crean o se descubren?
• ¿Cómo se define el concepto de verdad en matemáticas
• ¿Cómo fundamentar correctamente un edificio intelectual tan sofisticado como las matemáticas?
Estos cuestionamientos dieron lugar a un gran debate durante la segunda mitad del siglo XIX y primera del XX.
Para empezar esta historia, explicaremos las dos posturas que existen sobre la esencia de los objetos matemáticos: aquella que sostiene que se construyen a través de procedimientos intuitivos y aquella que, por el contrario, afirma que los objetos matemáticos se conciben o se entienden como parte de una totalidad existente al margen de quien los estudia, es decir, el matemático. Esta segunda postura se conoce como platonismo matemático y ha sido muy relevante en el desarrollo de las matemáticas modernas durante el siglo XX. El afirmar que los objetos matemáticos gozan de una existencia real —análoga en algún sentido a la existencia de los objetos físicos— permite concebir un "universo matemático" independiente de las técnicas o los procedimientos que se usen para estudiarlo.
Son muchos los intentos a lo largo de la historia por mecanizar el razonamiento matemático y probar que estaba libre de contradicciones, es decir, por exhibir fundamentos sólidos sobre los cuales podía erigirse.
El trabajo más importante en este campo comenzó a finales del siglo XIX, cuando los objetos matemáticos empezaron a definirse en términos de conjuntos. Por consiguiente, se intentó definir los números, las funciones y los distintos espacios en términos de conjuntos, con el fin de tener un sistema de reglas para deducir los teoremas a partir de conjuntos pequeños de axiomas y lograr, así, un sistema matemático riguroso.
La teoría de conjuntos se desarrolló con el trabajo de Cantor —un matemático alemán que vivió de 1845 a 1918—, aunque varios matemáticos ya habían trabajado en la orientación "conjuntista" de las matemáticas. La teoría de conjuntos tiene sus raíces en el análisis real, en la teoría de series trigonométricas y, en particular, en la representación de funciones discontinuas a través de series de Fourier y en la caracterización de los conjuntos de puntos de discontinuidad.
Cuando Cantor descubrió, en 1873, que el conjunto de los números reales no es numerable, es decir, que no puede ponerse en correspondencia uno a uno con el conjunto de los números naturales, la concepción que hasta entonces se tenía del infinito cambió radicalmente. Surgieron muchos conceptos nuevos a partir del trabajo de Cantor, como el de conjunto bien ordenado, número ordinal, número cardinal y número transfinito. Cada vez era más fácil caracterizar a los objetos matemáticos en términos de conjuntos.
Pero con la teoría de conjuntos llegaron también las paradojas. A mediados del siglo XIX, ya era bastante grande el grupo de matemáticos y filósofos muy importantes que sostenían una discusión sobre los fundamentos de las matemáticas. El objetivo era eliminar las paradojas y discutir qué era o no aceptable en las matemáticas. Por ejemplo, el axioma de elección o la hipótesis del continuo tenían que ser discutidos.
Las paradojas nacían de asumir que cualquier colección de objetos —tangibles o pensables— que satisficiera una propiedad era un conjunto. Y así había una correspondencia entre conjuntos y propiedades, pero Bertrand Russell —filósofo y matemático galés— mostró que al menos había una propiedad,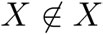 
, que no determina ningún conjunto si no se quiere caer en una tremenda contradicción.
Una manera de replantear este problema es con la paradoja que ya habíamos revisado anteriormente: "el barbero de un pueblo afeita a todas las personas del pueblo que no se afeitan a sí mismas y sólo a ésas", ¿debe el barbero afeitarse a sí mismo?
Sea A el conjunto de todas las personas que no se afeitan a sí mismas, entonces podemos hacer la siguiente argumentación: el barbero pertenece a A si y sólo si no se afeita a sí mismo, si y sólo si lo afeita el barbero, si y sólo si se afeita a sí mismo, si y sólo si no pertenece al conjunto A. Entonces el barbero es elemento del conjunto A si y sólo si no es elemento del conjunto A.
Pasa lo mismo al definir el conjunto de todos los conjuntos que no se pertenecen a sí mismos y preguntarse si dicho conjunto pertenece a sí mismo. Con esta paradoja, Russell planteó la imposibilidad de asociar un conjunto a cada propiedad.
Para resolver la paradoja, Russell desarrolló la teoría de tipos, en la que la idea básica es establecer tipos o clases que, a la vez, contienen tipos o clases de una jerarquía inferior.
La necesidad de resolver las paradojas tuvo como consecuencia determinar que el camino más sólido para desarrollar las matemáticas era establecer una axiomática para la teoría de conjuntos, similar a la que se tenía para la geometría.
Hubo varias propuestas: la de Zermelo-Fraenkel y la de von Neumann-Bernays-Gödel. Por otra parte, el matemático alemán David Hilbert (1862-1943), que en 1899 había publicado una axiomática para la geometría euclidiana —más completa que la que hiciera el propio Euclides—, desarrolló los conceptos necesarios para el estudio de las propiedades formales de las teorías axiomáticas en lo que él llamó teoría de prueba.
La idea de Hilbert era genial pues se trataba de conseguir una formalización completa de las matemáticas, en particular de la teoría de conjuntos o de la aritmética, de manera que al unir la lógica con una interpretación formal de una teoría matemática concreta, se pudiera formalizar cualquier afirmación de dicha teoría. Esto quiere decir que cualquier afirmación podría formalizarse como una sucesión finita de fórmulas abstractas cuyos símbolos, aislados y sin interpretación, carecerían de significado por sí mismos, evitando así la aparición de paradojas.
Hasta antes del siglo XIX, la intuición era la forma de saber si un sistema axiomático pudiera llevar a contradicciones o no. Euclides formuló sus axiomas para la geometría tomando como modelo la realidad física. Pero, conforme los sistemas axiomáticos se fueron haciendo más abstractos, la intuición y la experiencia dejaron de ser la forma adecuada de verificar si dichos sistemas eran consistentes o no.
Así que una de las cosas más importantes al trabajar con un sistema axiomático es determinar si es consistente o no.Y esta pregunta se hace y se fue haciendo extensiva a todas las matemáticas, a lo largo de la historia: ¿están las matemáticas construidas sobre bases y fundamentos sólidos? ¿Cómo saber que las matemáticas no contienen ninguna contradicción en su seno? Se trataba, a fin de cuentas, de garantizar que cualquier afirmación verdadera pudiera ser demostrada dentro del sistema.
Un personaje muy importante en la sistematización rigurosa de las matemáticas es Giuseppe Peano, matemático y filósofo italiano que vivió de 1858 a 1932. Peano hizo un análisis muy serio del proceso demostrativo de las matemáticas: estableció la formulación axiomática de la aritmética a través de un conjunto de cinco axiomas que hoy se conocen como los axiomas de Peano y que definen a los números naturales, en términos de la teoría de conjuntos. Los axiomas de Peano son:
1. El número 0 es natural.
2. Si n es un número natural, entonces S (n) —el sucesor de n— también es un número natural.
3. El número 0 no es sucesor de ningún número natural.
4. Si para dos números naturales m y n sucede que (m) = (n), es decir, sus sucesores son iguales, entonces m = n.
5. Si dada una propiedad p, sucede que:
a] el número 0 cumple la propiedad p,
b] cada vez que un natural n cumple la propiedad p, ocurre que S (n) también cumple la propiedad p,
entonces todos los números naturales cumplen la propiedad p.
Este último axioma se conoce como el principio de inducción. Durante la segunda mitad del siglo XIX y la primera del XX, el "edificio matemático" fue adquiriendo cada vez más rigor. Fueron muchísimos los matemáticos y filósofos que participaron en la discusión sobre los fundamentos de las matemáticas, con posturas a veces antagónicas y otras veces complementarias.
Y entre estas posturas pueden distinguirse tres que son cruciales y en las que las personas de las que hemos venido hablando pueden ubicarse: el logicismo, el intuicionismo y el formalismo.
El logicismo fue iniciado por Gottlob Frege, un filósofo y matemático alemán que vivió de 1848 a 1925, pero sus máximos exponentes fueron el galés Bertrand Russell (1872-1970) y el inglés Alfred N. Whitehead (1861-1947). El objetivo principal de los logicistas era mostrar que las matemáticas clásicas eran una parte de la lógica, así que la pregunta ¿están las matemáticas libres de contradicciones? se replanteaba como ¿está la lógica libre de contradicciones? Russell y Whitehead escribieron, entre muchas otras obras, Principia Mathematica, y en ella intentaron mostrar que todas las matemáticas conocidas hasta ese momento se podían derivar de un sistema axiomático que ellos proponían en sus Principia. Sin embargo, nunca pudieron probar que la lógica estaba libre de contradicciones.
El intuicionismo comenzó alrededor de 1908 con un matemático holandés llamado Luitzen Egbertus Jan Brouwer (1881-1966). Mientras que los logicistas jamás habían dudado de la solidez de las matemáticas, los intuicionistas cuestionaron —desde el principio— las matemáticas clásicas y propusieron reconstruirlas por completo, partiendo de cero.
El formalismo existía ya en el siglo XIX, pero, sin duda, su exponente más importante es David Hilbert. Los formalistas propusieron que era necesario formalizar todos los sistemas axiomáticos.
Es interesante ver que, tanto los logicistas como los formalistas, intentaron formalizar todas las ramas de las matemáticas por diferentes razones. Los primeros querían usar la formalización para mostrar que ese campo pertenecía a la lógica; los segundos, para probar matemáticamente que en esa rama no había contradicciones.
Russell y Whitehead construyeron un sistema lógico intentando que de él pudiese derivar toda la matemática: ése fue el sistema que expusieron en sus Principia. ¿Era posible deducir todas las verdades matemáticas a partir de ese sistema? ¿Cómo podían tener la certeza de que ese sistema era consistente, es decir, que no podían deducirse contradicciones a partir de él? Este último cuestionamiento era tan importante que Hilbert lo propuso a los matemáticos como una de las preguntas abiertas más importantes para ser contestada en el siglo XX.
El intuicionismo asumió como suyas las críticas que emergieron frente al carácter abstracto de las matemáticas. Con Brouwer se estructuró una visión sobre la naturaleza de las matemáticas, presente también entre los matemáticos decimonónicos como Kronecker y Baire. Los intuicionistas se colocaban en un terreno opuesto, de alguna manera, al formalismo y al logicismo, pues para ellos era indispensable recurrir a la intuición.
Mientras que los logicistas elevaban la lógica a una categoría muy alta, para los intuicionistas se trataba tan sólo de un instrumento absolutamente accesorio.
Los intuicionistas no trataban de probar la consistencia de la matemática sino de hacer "matemática verdadera", apegada a la intuición introspectiva.
Si bien los intuicionistas argumentaban —permanentemente— que no estaban preocupados por los fundamentos de las matemáticas, siempre trabajaron por hacer estable el edificio matemático en el que se movían. Las ideas en la filosofía de las matemáticas y, en particular, en torno a los fundamentos, nunca han sido blancas o negras; todas fueron entretejiéndose.
La historia no tuvo un final feliz. En 1931, Kurt Gödel mostró al mundo en su artículo "Sobre proposiciones formalmente indecidibles en Principia Mathematica y sistemas relacionados" que no es posible fundamentar las matemáticas a través de un sistema formal que sea consistente y completo; dicho de otra manera, ningún sistema formal que contenga a la aritmética puede probar su propia consistencia, como se verá en la sección 4.11.
Gödel evidenció una limitación fundamental del método axiomático al probar que, para cualquier conjunto consistente en axiomas que contenga a los axiomas de la aritmética, existen afirmaciones verdaderas que no pueden deducirse a partir de dicho conjunto.
En matemáticas, hay muchos enunciados que parecen evidentes para los que no se ha encontrado un contraejemplo y, sin embargo, no han podido ser demostrados. Un ejemplo es la conjetura de Golbach, que afirma que todo número par mayor que dos es la suma de dos números primos.
El debate sobre los fundamentos sobrepasó la necesidad de elegir alguna de las posturas enfrentadas. Legó, tanto a matemáticos como a filósofos, el conocimiento de hasta dónde podía llegarse en la formalización de teorías matemáticas, a través de la lógica, y puso de manifiesto la diferencia entre la postura constructivista y la concepción formalista —que considera a los objetos matemáticos como existentes—, que no estaba tan clara antes del siglo XIX. Esta definición ha sido una de las contribuciones más importantes del debate sobre los fundamentos.
Si bien el logicismo y el formalismo no lograron fundamentar totalmente las matemáticas, el desarrollo en el campo de la filosofía de las matemáticas ha tenido repercusiones muy importantes en otros ámbitos. El trabajo realizado por estos filósofos y matemáticos ha contribuido en otros campos como la lingüística, el ánalisis del razonamiento deductivo, la informática y la computación.
