En el contexto matemático, un modelo es una herramienta que facilita la descripción, representación, explicación, predicción, discusión o evolución particular de un objeto, proceso, sistema o fenómeno. En esta sección veremos diferentes herramientas matemáticas que pueden usarse para la modelación y que hay una que, claramente, es la más potente: la ecuación diferencial. Antes de llegar a ello, veremos primero unos ejemplos que muestran la gran versatilidad de los conceptos.
Un número es impar si no es divisible entre dos. La suma de dos impares es par, como se ve, por ejemplo, en 3 + 5 = 8. Pero si quisiéramos hacer una demostración de ello, necesitamos tener una expresión que nos modele el número impar en general. Ésta existe y es un término de la forma:
2n + 1
donde n es cualquier entero. Para diferentes valores de n obtenemos diferentes números impares, es más, obtenemos todos los impares y sólo impares. Con este modelo es fácil comprobar que, en general, la suma de dos impares —digamos 2m + 1 y 2n + 1— es par:
(2m + 1) + (2n + 1) = 2m + 2n + 2 = 2(m + n + 1),
ya que el lado derecho es un múltiplo de 2.
Veremos ahora cómo una ecuación puede modelar una situación interesante. El principio que impulsa los cohetes espaciales se basa en la conservación del impulso: si en el espacio vacío —donde no actúa la gravedad— un astronauta lanza un objeto, se impulsa en la dirección opuesta. El cohete trae combustible y, al quemarlo, expulsa gas a gran velocidad ve—la velocidad de emisión— al espacio, lo que impulsa al cohete. La ecuación de Tsiolkovski (5) representa el aumento en la velocidad Δv que puede alcanzar un cohete al quemar todo su combustible. La ecuación relaciona la masa total inicial minicial y la masa final mfinal después de consumir el combustible, con las velocidades Δv y ve.
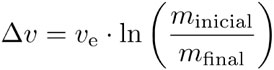 (5)
(5)
En esta ecuación aparece la función de logaritmo natural. Por ejemplo, si el 80% de la masa total es combustible, entonces:
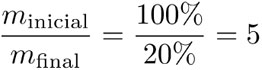
y como 1n(5)es aproximadamente 1.6, el cohete alcanzará 1.6 veces la velocidad de emisión. La velocidad de expulsión puede alcanzar hasta los 4 400 metros por segundo en motores que usan hidrógeno y oxígeno; con ello, el cohete alcanzará una velocidad de más de 25 mil kilómetros por hora. Para un cálculo realista hay que tomar en cuenta que el cohete sale de la Tierra y usa gran parte del combustible para alejarse de ella, es decir, para elevarse en contra de la fuerza de gravedad. Para ese cálculo necesitaríamos otra ecuación.
Como vemos, la ecuación puede ser muy útil para calcular ciertas cantidades, pero al mismo tiempo tiene sus limitaciones —en este caso sólo sirve para el espacio vacío, así que su uso real siempre será aproximado—. Lo anterior es la típica característica de un modelo: permite hacer un cálculo que, usualmente, es simplificado y, a partir de él, hacer predicciones. Toda la aeronáutica espacial se basa en modelos que tienen que ser muy buenos, dado que los experimentos reales son muy costosos.