Sean A y B dos eventos en cualquier espacio probabilístico. Supongamos que al realizar el experimento nos informan que el evento A ocurrió. ¿Eso nos dice algo acerca del evento B? En general sí. Por ejemplo, consideremos estos dos eventos en el experimento de lanzar un dado:
A = "el resultado es par" y
B = "el resultado es mayor que 3".
La probabilidad de A es claramente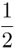 
y la de B también es 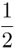. Pero si alguien nos informa que A ocurrió, ¿seguirá B teniendo la misma probabilidad? La respuesta es no. Saber que el resultado es par implica que ya sólo quedan tres posibilidades: 2, 4 y 6 y, como éstas son equiprobables, la probabilidad de que el resultado sea mayor que 3 es ahora 
.
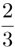¿Entonces la probabilidad del evento B no estaba bien definida porque antes era 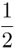y ahora es 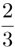. ? En realidad lo que sucede es que saber la ocurrencia del evento A nos lleva a una nueva situación probabilística, a un nuevo espacio de probabilidad. El espacio muestral en la nueva situación ya no es {1, 2, 3, 4, 5, 6} sino {2, 4, 6}. Como estos cambios de espacio probabilístico se dan mucho en el estudio de la probabilidad, se ha desarrollado un concepto que permite referirse a estas situaciones nuevas manteniendo el lenguaje de la situación original, lo cual resulta cómodo en la práctica. Se trata del concepto de probabilidad condicional. El evento de que ocurra B cuando se garantiza la ocurrencia de A, se denomina "B dado A" y se denota por B|A. Las probabilidades de estos eventos son: 
, 
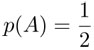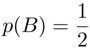y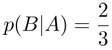 
. La probabilidad condicional puede definirse así:
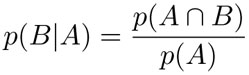
y se puede interpretar como otro espacio de probabilidad donde el espacio muestral es A. Observemos que esta relación se cumple en el ejemplo anterior. En efecto,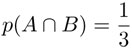 
, pues A ∩ B = {4, 6} y, por tanto:
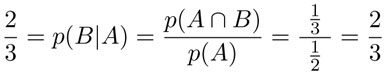
El concepto intuitivo de probabilidad condicional corresponde de manera adecuada a la definición formal.
La probabilidad condicional es uno de los dos conceptos claves de la teoría de la probabilidad. El otro es el de eventos independientes, que se describe a continuación.
Consideremos otra vez el experimento de lanzar un dado pero ahora con dos nuevos eventos A y B:
A = "el resultado es impar" y
B = "el resultado es 3 o 4".
Entonces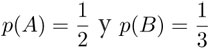 
. Saber que A ocurre nos dice que las únicas posibilidades son 1 , 3 y 5 , todas igualmente probables; por tanto, 
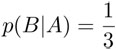. En este caso la probabilidad de B y la de " B dado A" son iguales. En estas circunstancias se dice que B es independiente de A. En términos de probabilidades, decimos que B es independiente de A si p(B|A) = p(B) . Usando la definición de probabilidad condicional obtenemos que si B es independiente de A, entonces:
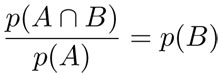
o en forma equivalente:
Esto muestra que el concepto de eventos independientes es simétrico, es decir, B es independiente de A si y sólo si A es independiente de B . Por tal motivo, se habla de eventos independientes sin especificar cuál de ellos es independiente del otro. Como corolario obtenemos que si A y B son eventos independientes, entonces p(B|A) = p(B) y p(A|B) = p(A) p(A|B) = p(A) .
Se dice que dos eventos son mutuamente excluyentes si la ocurrencia de cualquiera de ellos implica que la ocurrencia del otro es imposible. Por ejemplo, en el experimento de lanzar un dado y observar el número en la cara de arriba, los siguientes eventos A = "el número obtenido es par" y B = "el número obtenido es 5" son mutuamente excluyentes. Que dos eventos sean mutuamente excluyentes equivale a que los conjuntos de resultados que los representan son ajenos, es decir, dos eventos A y B son mutuamente excluyentes si y sólo si A ∩ B = Ø. Es importante observar que este concepto no es probabilístico sino únicamente lógico y que la probabilidad no interviene en su definición; sin embargo, con frecuencia se comete el error de confundirlo con la independencia de eventos explicada anteriormente.
Una variable aleatoria es una función real definida en el espacio muestral de un espacio probabilístico (Ω, Σ, p), en otras palabras, es una función:
Las variables aleatorias, a pesar de ser funciones, se suelen denotar con letras X, Y, . . . mayúsculas en lugar de con una f . Se dice que dos variables aleatorias X1 y X2 son independientes si los eventos que se pueden definir con una y otra son siempre independientes, es decir, si eventos como {ω ∈ Ω : a1 ≤ X1(ω) ≤ b1} y {ω ∈ Ω : a2 ≤ X2(ω) ≤ b2}son independientes.
Intuitivamente, dos variables aleatorias son independientes si el saber algo de una de ellas no nos da ninguna información acerca de la otra. Por ejemplo, en el experimento de lanzar dos dados, saber el resultado de uno de ellos no nos da información acerca del otro. Las variables aleatorias X1 y X2 definidas como el número en la cara superior del primer dado y el mismo número pero del segundo dado, respectivamente, son variables independientes.
Las variables independientes desempeñan un papel fundamental en el teorema del límite central, uno de los resultados más importantes y útiles de la probabilidad, que se aplica en la estadística.
