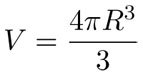La cuadratura de la parábola, al igual que el cálculo del volumen de la esfera, se debe al genio de Arquímedes. Aquí la obtendremos recurriendo a un procedimiento general para obtener áreas de regiones delimitadas por curvas, esencia del cálculo integral. Este método nos llevará, por un camino diferente al de la sección anterior, hasta obtener los volúmenes del cono y la esfera.
Para encontrar la cuadratura de la parábola necesitaremos la igualdad:
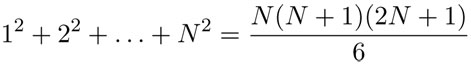
que es válida para todo entero positivo N . Otra manera de expresar esta igualdad es usando la notación de suma:
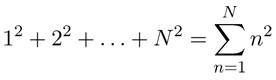
por lo que la fórmula puede también escribirse así:
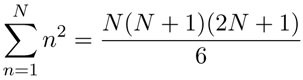
Esta fórmula suele demostrarse por el llamado método de inducción, que consta de dos pasos:
1. Se comprueba que la fórmula es válida para N = 1.
2. Suponiendo que la fórmula es válida para algún entero positivo N, se prueba que también será válida para el siguiente entero N + 1 .
El primer paso se cumple porque, para N = 1, ambos lados de la igualdad valen 1, en efecto:
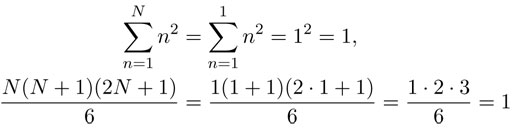
Ahora, supongamos que la igualdad se cumple para algún entero positivo N y probemos que entonces también se cumple para N + 1.
Esto completa la demostración por inducción.
Cuadrar la parábola significa encontrar el área encerrada por ella y una recta. Simplificaremos el proceso al pasar directamente a obtener el área debajo de una parábola específica, la que corresponde a la gráfica de y = x2. Denotemos por A al área bajo la parábola entre 0 y a.
Vamos a demostrar que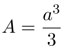 
. Para ello, dividimos el intervalo [0, a] en N partes iguales y dibujamos dos gráficas formadas por rectas horizontales —una por debajo de la parábola y otra por arriba—, como se ilustra en la figura 2.61.
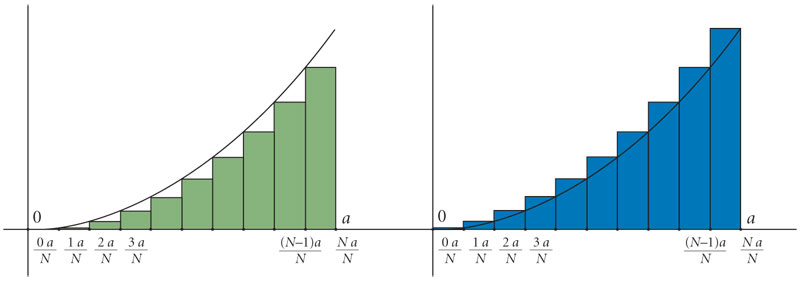
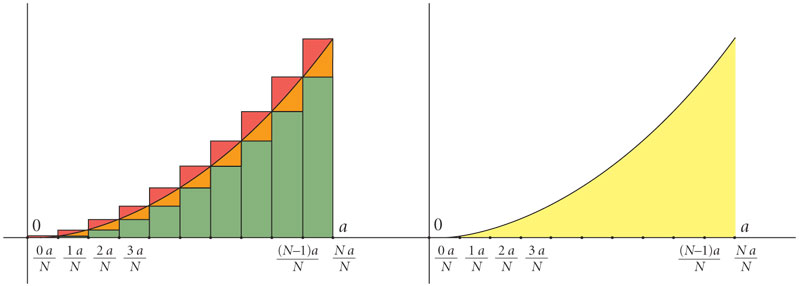
Entonces, A es mayor que el área de los rectángulos verdes y menor que el área de los rectángulos rojos. La suma de las áreas de los rectángulos verdes es:
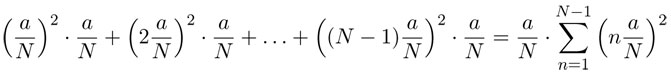
y la de los rectángulos rojos:
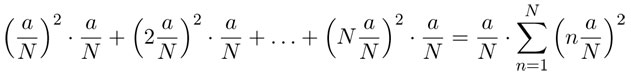
Por lo tanto, se tienen las siguientes desigualdades para el área A bajo la parábola:
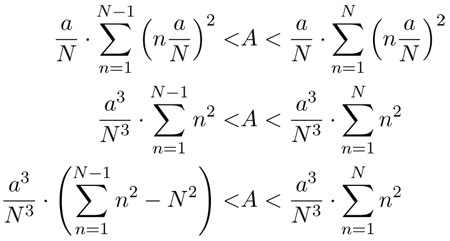
Al aplicar la fórmula que demostramos anteriormente por inducción y que nos da la suma de los primeros cuadrados, obtenemos las siguientes desigualdades:
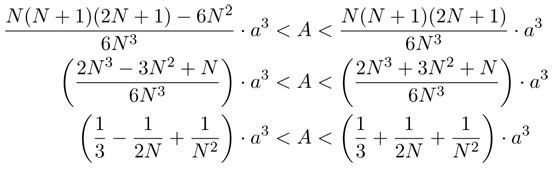
Finalmente, como estas desigualdades se cumplen para cualquier entero positivo N, tomando "uno" suficientemente grande podemos hacer que, tanto el lado izquierdo como el derecho, estén tan cercanos a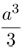 
como queramos. Y entonces:
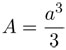
que es lo que queríamos demostrar.
El método anterior es un proceso infinito de aproximación que nos permite obtener un resultado exacto, y contiene la esencia del cálculo integral que Arquímedes ya usaba en el siglo III a.C. y, que Newton y luego Leibniz —al formalizarlo—, generalizaron casi dos mil años más tarde. En la notación moderna del cálculo integral, inventada por Leibniz, este resultado se expresa así:
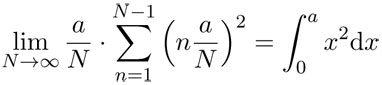
y debe leerse como "la integral de cero a a de x2 con respecto a x". La integral se convierte en el límite de cualquier suma cuando el número de particiones N tiende a infinito —y por lo tanto, el ancho de las particiones tiende a cero.
Intuitivamente, la integral se interpreta como una "suma infinita" de cantidades "infinitamente pequeñas" o bien, "infinitesimales". Aunque esta manera de hablar no es matemáticamente rigurosa, se utiliza con frecuencia como una forma abreviada de indicar el proceso con el que se llega —sí, rigurosamente— al resultado.
El método de integración usado para alcanzar la cuadratura de la parábola nos permite obtener fácilmente, como corolarios, dos resultados ya conocidos: el volumen del cono y el de la esfera.
Para encontrar el volumen del cono cuya altura es H y cuya base tiene radio R, lo partimos en una "infinidad" de discos —cilindros circulares— de grosor infinitesimal" dh y radio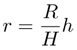 
, donde h varía de 0 a H . Entonces, el volumen del cono es la "suma infinita" de los volúmenes de todos esos discos. En la notación de Leibniz, lo anterior se escribe como:
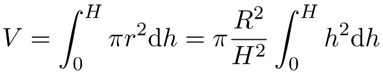
Salvo por la constante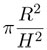 
y un cambio en el nombre de la variable —x por h—, esta es la misma integral que se usó para obtener la cuadratura de la parábola, de donde sabemos que:
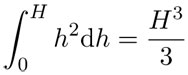
En consecuencia, el volumen del cono es:
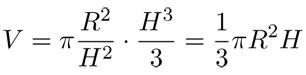
En forma análoga, partiendo del resultado de que el área de una superficie esférica de radio r es 4πr2, el cálculo del volumen de la esfera de radio R es equivalente a la cuadratura de la parábola y = 4πr2 entre 0 y R. En efecto, la esfera se puede considerar como la suma de una infinidad de superficies esféricas de grosor infinitesimal dr y de área —variable— 4πr2 con r entre 0 y R. Por consiguiente, el volumen de la esfera puede calcularse también como una "suma infinita" de cantidades "infinitesimales":
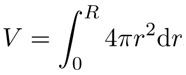
Y de nuevo, salvo por la constante 4π y un cambio en el nombre de la variable —x por r—, esta "suma infinita" de "infinitesimales", que hoy llamamos integral, es la misma que se usa para cuadrar la parábola. Por lo tanto, el volumen de la esfera de radio R es:
