Civilizaciones tan antiguas como la babilónica, la egipcia, la china y la hindú, reconocieron que había ciertas relaciones entre las dimensiones de algunas figuras geométricas que se mantenían constantes aunque su tamaño variara, es decir, que eran independientes del tamaño de la figura.
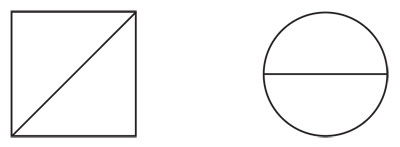
Por ejemplo, la diagonal de un cuadrado mide un poco menos que una y media veces su lado, independientemente de si el cuadrado es grande o pequeño. También el perímetro de una circunferencia es poco más que tres veces su diámetro, sin importar si la circunferencia es grande o minúscula como una retina. Se trata de relaciones, razones o proporciones fijas —que no se alteran aunque varíe el tamaño de las figuras—, que sólo dependen de su forma. Estas relaciones permiten calcular, por ejemplo, la diagonal de una plaza cuadrada cuyos lados miden 80 metros. A través de sucesivas mediciones podríamos comprobar que la relación entre la diagonal y el lado de un cuadrado es mayor que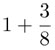 
y menor que 
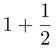. Por lo tanto, la diagonal de la plaza sería mayor que 110 metros y menor que 120 metros. Pero… ¿cuánto mide exactamente la diagonal de la plaza? Para responderlo, tendríamos que saber cuántas veces es mayor la diagonal de un cuadrado que su lado, es decir, tendríamos que conocer con exactitud la relación entre estas dos dimensiones.
El concepto de número que tenía el hombre de la Antigüedad se limitaba a las fracciones —cocientes de números enteros—, demasiado primitivas para representar cantidades —como los números irracionales— que no pueden ser expresadas mediante fracciones. En particular, fueron los pitagóricos quienes, desde entonces, descubrieron que esta razón o proporción entre la diagonal y el lado de un cuadrado no puede expresarse mediante una fracción, así que no tuvieron otro remedio que hacerlo con algún símbolo y estimar su valor usando fracciones. Hoy en día representamos dicha relación como √2 y sabemos que 1.414213 < √2 < 1.414214 .
De manera análoga, la relación entre el perímetro de una circunferencia y su diámetro tampoco puede expresarse con fracciones. De hecho, como veremos más adelante, se trata de una relación aún más compleja. Las civilizaciones antiguas intentaron expresarla a partir de fracciones cada vez más exactas, pero eran sólo meras aproximaciones de algo cuya definición, como número, escapaba al lenguaje matemático de la época. No fue sino hasta el esplendor de la civilización helénica cuando se llegó a un concepto y una definición precisa de dicha relación, razón o proporción, que hoy llamamos π e identificamos con los famosos dígitos 3.1416.
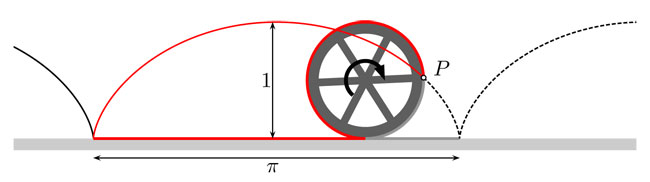
Los babilonios usaron durante un tiempo al 3 como una aproximación práctica; más adelante y al mejorarla, adoptaron el valor 
, equivalente a 3.125. El papiro Rihnd —que data de 1650 a.C.— incluye una aproximación aún más cercana, equivalente a 3.16049. Estas estimaciones eran el resultado de cálculos de perímetros de figuras formadas por segmentos —más o menos parecidas al círculo— y que representaban valores útiles; sin embargo, no respondían a un concepto matemático bien definido.
La definición correcta y el primer cálculo de esta relación como un resultado matemático se deben a Arquímedes de Siracusa —siglo III a.C.—. Él demuestra, apoyado en los conocimientos geométricos de la época que, efectivamente, la relación entre el perímetro y el diámetro de la circunferencia es independiente del tamaño de la misma —y se mantiene aunque el tamaño cambie—, y en seguida procede a realizar un cálculo riguroso de la relación demostrando que se encuentra entre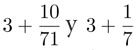 
. El uso de la letra π—inicial que denota perímetro en griego— es mucho más reciente y proviene del matemático galés William Jones, quien la usó por primera vez en 1706. Esta notación se popularizó luego a través de los trabajos de Leonhard Euler.
Lo relevante del trabajo de Arquímedes no son los valores concretos que obtuvo, sino el método que inventó para ello y con el que abrió la posibilidad de obtener el valor de π con tanta precisión como se desee, aunque el proceso pueda ser lento por la dificultad de los cálculos requeridos. Es importante tomar en cuenta que, para obtener su resultado, Arquímedes tuvo que realizar varias estimaciones de fracciones y raíces cuadradas —cuya expresión decimal era entonces desconocida— en forma de laboriosas desigualdades entre fracciones. Actualmente, el método de Arquímedes para estimar π puede utilizarse perfectamente en una computadora para obtener estimaciones bastante más precisas que las del célebre siracusano.
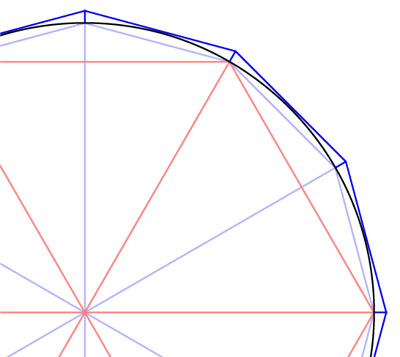
El método de Arquímedes para definir y calcular π consiste en comparar el perímetro de la circunferencia con los de dos polígonos regulares, uno inscrito y otro circunscrito a ella, como se muestra en la figura.
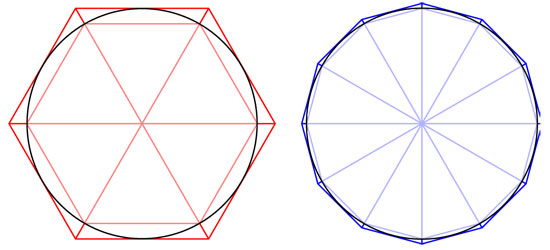
Al utilizar resultados de la geometría euclidiana, Arquímedes demuestra que el perímetro de la circunferencia debe ser mayor que el del polígono inscrito y menor que el del circunscrito. También demuestra que la diferencia entre ambos puede hacerse tan pequeña como se desee al considerar polígonos con un número muy grande de lados. Estas ideas contienen no sólo el germen del concepto de límite utilizado en el cálculo moderno sino, también, la manera de tratarlo con absoluto rigor lógico.
Analicemos una circunferencia de radio 1 y consideremos π como la mitad de su perímetro. Entonces, el lado del hexágono inscrito es L = 1 y, por el teorema de Pitágoras, su apotema —la distancia del centro a cada lado— es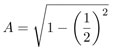 
. Por semejanza de triángulos, el lado del hexágono circunscrito mide 
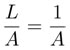. De ahí se obtienen las siguientes desigualdades:
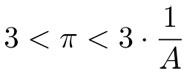
Si ahora se consideran los dodecágonos regulares —inscrito y circunscrito— y se usa nuevamente el teorema de Pitágoras, resulta que el lado del dodecágono inscrito es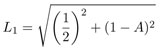 
, mientras que su apotema es 
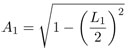; por semejanza de triángulos se obtiene que el lado del dodecágono circunscrito es 
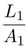. Al sumar los lados, se obtienen las siguientes desigualdades:
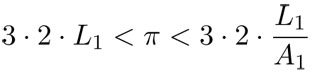
Si se siguen construyendo polígonos regulares de 24 , 48, 96, ... lados, y cada vez se divide el ángulo interno entre dos, se tienen las desigualdades:
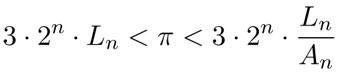
donde Ln es el lado del polígono regular con 6 · 2n lados y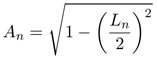 
es su apotema. El valor de Ln se puede obtener recursivamente —que quiere decir "repetir indefinidamente la aplicación de"— mediante la fórmula 
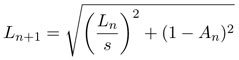, consecuencia directa del teorema de Pitágoras. Estas fórmulas ofrecen un algoritmo para calcular aproximaciones de π con cualquier grado de precisión. La siguiente tabla muestra las desigualdades —que se obtienen al usar este procedimiento— expresadas con 6 decimales:
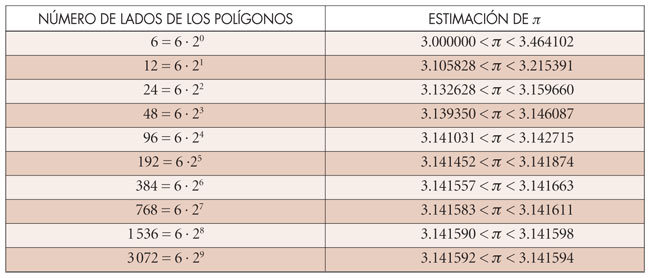
Las desigualdades correspondientes al polígono de 96 lados son ligeramente mejores a las que obtuvo Arquímedes con el mismo polígono: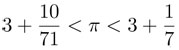 
—aproximadamente 3.140845 < π < 3.142857, con precisión de seis decimales. La aproximación que se obtiene con el polígono de 3072 lados corresponde a la que obtuvo en el año 263 d.C. el matemático chino Lui Hui.
Esfuerzos sucesivos en el cálculo han alcanzado más y más precisión. Primero fueron manuales y después se hicieron usando computadoras cada vez más potentes. En la actualidad, el récord en el cálculo de dígitos lo tiene Daisuke Takahashi, con más de dos y medio billones de cifras decimales. Cabe mencionar que estos esfuerzos no tienen ninguna importancia respecto al significado de π, sólo se hacen por el prestigio que da a los programadores y constructores de computadoras el llegar a ellos.
En cambio, es muy interesante saber que el número π aparece en una gran cantidad de resultados matemáticos, aparentemente, sin relación alguna con la circunferencia. Por ejemplo, se sabe que:
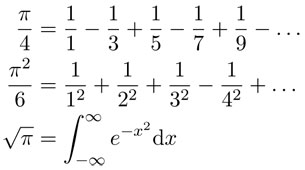
Arquímedes no sólo define y calcula π sino que usa su valor para expresar el área de la circunferencia y, también, el de volúmenes y áreas de conos, cilindros y esferas. Se trata de los primeros resultados de cálculos matemáticos precisos de áreas de figuras delimitadas por curvas y de superficies curvas que no pueden aplanarse sin alterar su área. La geometría de Euclides permitía obtener las áreas de regiones delimitadas por rectas, pero al intentar obtener las áreas de regiones con fronteras curvas se experimentaron grandes dificultades. Fue Arquímedes quien señaló el camino adecuado para resolverlas con un método que, a la larga, daría lugar a una de las teorías y herramientas matemáticas más poderosas: el cálculo integral.
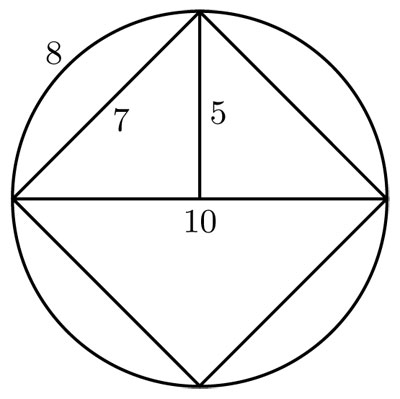
Para comprender la importancia de esta parte del trabajo de Arquímedes conviene repasar los problemas de "cuadraturas" que se plantearon los matemáticos griegos. "Cuadrar" una figura era encontrar un cuadrado —un rectángulo o un triángulo— cuya área fuera igual a la de la figura dada. El problema de la cuadratura del círculo se hizo famoso a través de los siglos al encontrar que resultaba imposible hacerlo únicamente con los métodos y elementos de la geometría de Euclides, es decir, sólo con regla y compás. Un caso especial de cuadratura que sí se obtuvo con los métodos euclidianos fue el de las llamadas lunas de Hipócrates de Quios —en el siglo V a.C.—, quien demostró que las figuras obtenidas por defecto de los semicírculos construidos sobre los catetos de un triángulo rectángulo ΔABC , y el semicírculo que tiene como diámetro la hipotenusa y pasa por el ángulo recto, tienen igual área que el triángulo ΔABC .
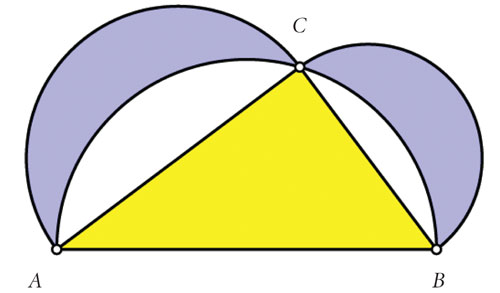
El resultado anterior es consecuencia directa del teorema de Pitágoras, aplicado no a los cuadrados construidos sobre los catetos y la hipotenusa, sino a los semicírculos. La suma de las áreas de los semicírculos —que tienen como diámetros a los catetos— es igual al área del semicírculo —cuyo diámetro es la hipotenusa—. La conclusión de Hipócrates se infiere observando que las lunas son el resultado de restar de los semicírculos pequeños las mismas regiones que hay que restar al semicírculo grande para obtener el triángulo.
Esta ingeniosa deducción dio esperanzas a los matemáticos griegos para poder obtener, mediante trucos ingeniosos, la cuadratura de otras figuras delimitadas por curvas, en particular la del círculo. Sin embargo fue imposible, como finalmente logró demostrar Ferdinand Lindemann en 1882. Los métodos euclidianos consisten fundamentalmente de construcciones —hechas con regla y compás— en correspondencia con operaciones algebraicas que incluyen la extracción de raíces cuadradas. Los números algebraicos son los que pueden obtenerse mediante este tipo de operaciones —a partir de los enteros—, mientras que se llama trascendentes a los que no se pueden obtener de esta manera. Lindemann demostró que π es un número trascendente y, por lo tanto, la cuadratura del círculo no puede obtenerse usando regla y compás.
Sin embargo, dos mil años antes Arquímedes vio que había otro camino para resolver las cuadraturas: uno mucho más general pero que requería de un concepto que él mismo no definió completamente, aunque contribuyó a crear, el de límite. Veamos en forma resumida cómo obtiene Arquímedes el área de un círculo de radio R.
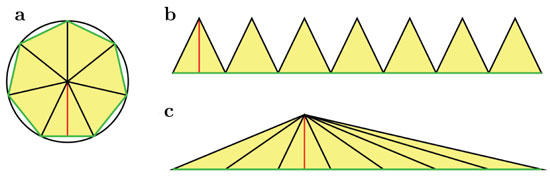
Si se inscribe un polígono regular de n lados en un círculo de radio R, su área es la de n triángulos isósceles de base L y altura A , es decir,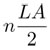 
, donde L es la longitud del lado del polígono y A el apotema. A medida que n aumenta, el área del polígono tiende a la del círculo y, al mismo tiempo, nL tiende al perímetro 2πr mientras el apotema A tiende al radio R. Por lo tanto:
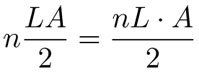tiende a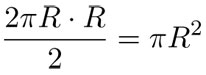 
cuando n tiende a ∞,
lo cual demuestra que el área del círculo de radio R es πR2 . Este argumento recurre al concepto moderno de "tender al límite", pero Arquímedes hizo su demostración utilizando desigualdades similares a las que usó para el cálculo de π.
En la siguiente sección se estudiará cómo aparece π en el cálculo de las áreas y volúmenes de cilindros, conos y esferas.
