¿Alguien está haciendo "cuernos"? No; así muestran los chinos el número seis. Hay diferentes convenciones sobre cómo se cuentan los números con las manos. Nosotros usamos el índice y el dedo medio para indicar el dos, mientras los europeos usan el índice y el pulgar. Contar es una de las habilidades que aprendemos desde muy pequeños y nos distingue de muchos animales, aunque no de todos; se sabe, por ejemplo, que los cuervos pueden contar bastante bien hasta 6 o 7.
Se dice que contar es una de las primeras actividades humanas: aunque todos contamos con los dedos, no se hace igual en todos lados. Precisamente por ello puede parecer sorprendente que, hoy en día, la gran mayoría de las culturas usan sólo los números arábigos para denotar cantidades. ¿Qué es lo que hace tan particularmente especiales a los números arábigos? ¿Por qué se impusieron sobre otras maneras de denotar? Preguntas como esta y otras se responderán en este apartado. Además, queremos evidenciar que la forma en que denotamos los números incide en la facilidad para hacer operaciones como sumar, restar o multiplicar. Descubriremos que la invención del cero juega un papel muy importante en todo lo anterior. El cero no sólo es la expresión numérica de la ausencia o la nada, sino que posibilita el reutilizar las mismas cifras para denotar unidades, decenas, centenas, miles o millones, como veremos más adelante.
El libro Discorsi de Galilei fue escrito en el año MDCXXXVIII, como se puede apreciar en la figura 2.3. Si bien ya no estamos familiarizados con esta manera de escribir los números —conocidos como números romanos—, para leer la fecha en la portada del libro hay que saber los valores de cada símbolo:
M = 1000, D = 500, C = 100, L = 50, X = 10, V = 5, I = 1
Entonces, podemos conocer, sin mayor dificultad, que el año de impresión es 1638.
Más difícil es traducir el año de impresión del libro De revolutionibus orbium coelestium de Copérnico, que es MDXLIII. Uno podría pensar que es igual a la suma de 1000 + 500 + 10 + 50 + 3 = 1563 pero, en realidad, fue impreso en 1543. Lo que sucede en este caso es que hay que aplicar una regla para el uso de los números romanos: restar un signo de menor valor cuando antecede a uno de mayor valor. Como el X está antes del L, se resta 10 a 50 y por ello se obtiene la cifra de 40.
Se complica el asunto si tratamos de multiplicar con números romanos. Por ejemplo:
XIX por XLVII = ?
¡Claro! X por XLVII es CDLXX, ya que simplemente se cambian los signos al multiplicar por diez. Así, lo que debemos calcular es:
CDLXX−XLVII + CDLXX
Sin embargo, ahora empezamos con algunas dificultades. Por ejemplo, CD + CD no es CCDD ni CDCD, sino DCCC . Luego, LXX + LXX no es LLXXXX, sino CXL. Los dos resultados anteriores se deben sumar y después restarles XLVII. Entonces, la operación sería:
DCCC + CXL − XLVII.
Se observa que el segundo sumando es C + XL , del cual se resta XL + VII . De esta manera, podemos quitar el término XL en ambos lados:
DCCC + C − VII.
Ahora bien, el cien —es decir, C— tiene que prestar X para poder restar VII. Usamos que C = XC + X . Además, X − VII = III . Finalmente, el resultado de la operación es:
DCCC + XC + III = DCCCXCIII.
Hicimos este cálculo sin transformar los números a nuestro sistema decimal, es decir, sin usar que XIX = 19 y XLVII = 47. El algoritmo que se enseña en la secundaria nos proporciona el resultado sin problema alguno:
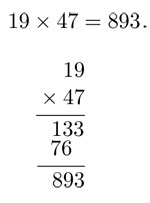
En efecto, 893 = DCCCXCIII . ¿Por qué parece más difícil trabajar con números romanos? No es solamente que no estamos tan familiarizados con estos símbolos sino, también, que no hay un algoritmo más o menos sencillo. En nuestro sistema decimal las mismas cifras se vuelven a reutilizar: la cifra 2 puede significar 20, 200 o dos millones en el número 2 480 225 . En este último número se observa algo peculiar: una de las cifras es un cero, así que tiene que expresar de manera explícita la ausencia de múltiplos de los miles. Si no tuviéramos un cero, el número no se podría escribir y se leería como 248225 que, obviamente, es algo equivocado.
El cero se inventó un par de veces en la historia de la humanidad. Aparece en el siglo III a.C. con la cultura babilónica y, también, con la maya en el siglo I d.C. Nuestra notación del cero se la debemos a la India, que la transmitió a los árabes. Todas estas culturas usaron un sistema posicional —donde se indica el valor de los símbolos según su posición—. En el número 22, el primero y el segundo 2 tienen significados diferentes, aunque se escriba exactamente el mismo símbolo en ambos casos. Esto es una gran ventaja: se usan sólo 10 símbolos. Además, las operaciones con los números expresados en este sistema se pueden explicar razonablemente bien y funcionan para todos los casos, sin importar la cantidad de dígitos.
El sistema posicional también tiene una desventaja: es fácil cambiar los números de lugar. Basta agregar, por ejemplo, un simple 4 antes del 720 para que el cheque ahora diga 4 720, ¡qué buen negocio sería! Por lo anterior, en los cheques y en cada documento importante que implique cantidades se suelen repetir los números en forma escrita: "720 y setecientos veinte".
Otra ventaja del sistema posicional es que resulta fácil escribir números muy grandes. En el sistema romano es muy difícil: se ponían rayas sobre los símbolos para indicar que ahora se trataba de una magnitud mayor. Por ejemplo,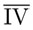 
significaba 4 000 y 
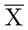= 10 000. En nuestro sistema no tenemos dificultad para representar un millón o un millón de millones, término que se conoce en español como billón. ¡El sistema no tiene límites! Por ejemplo, la masa del Sol es aproximadamente de:
1 990 000 000 000 000 000 000 000 000 000 kg
Notemos que usualmente se ponen comas o se incluyen espacios en blanco para indicar grupos de tres y no perder la cuenta. En la escritura romana, la misma cantidad tendría que representarse como:
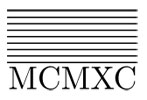
es decir, como 1990 con nueve rayas encima. Pero aun en el sistema decimal, un número así de grande es difícil de leer y para eso se usa la notación científica:
1 990 000 000 000 000 000 000 000 000 000 kg = 199 · 1028 kg
es decir, el número 199 seguido de 28 ceros y que se lee como "199 por diez a la veintiocho".
El ábaco que se muestra en la figura 2.4 se basa también en el sistema decimal. Como se observa, tiene varias hileras usualmente divididas en dos partes: una de cinco canicas y otra de sólo dos. Las primeras valen uno —diez, cien, mil, etc. — mientras las de dos valen cinco —cincuenta, quinientos, cinco mil, etcétera.
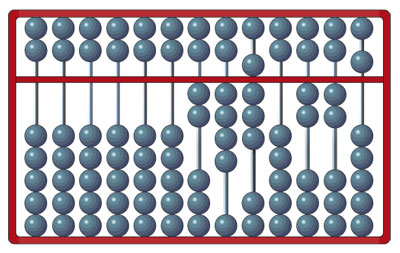
En la figura 2.5 se muestra el número 2 480 225. Alguien experimentado en el uso del ábaco es muy rápido al efectuar sumas y, razonablemente rápido al hacer multiplicaciones. Cabe mencionar que en el fondo, emplea los mismos procedimientos que nos enseñan a nosotros.
Dichos procedimientos son muy naturales. Por ejemplo, si queremos sumar 493 más 2 865, es claro que la suma tendrá: 3 + 5 = 8 unidades, 9 + 6 = 15 decenas, 4 + 8 = 12 centenas y 2 + 0 = 2 miles. Pero 15 decenas son una centena y 5 decenas. Así que se debe aumentar el número de centenas por uno: tenemos 5 decenas y 12 + 1 = 13 centenas. Éstas son a la vez un millar y 3 centenas. Tenemos entonces 3 millares, 3 centenas, 5 decenas y 8 unidades, es decir 3 358. En el procedimiento que se aprende en la primaria, el razonamiento anterior se repite una y otra vez hasta que se hace en automático, de tal manera que ya no haya que pensar en él cada vez.
Con la multiplicación sucede algo similar: se hace de manera muy automatizada. En el fondo, hay una necesidad de hacerlo justo así y no de otra manera. Por ejemplo, si se quiere multiplicar 19 por 47 —el ejemplo que hicimos con los números romanos—, debemos calcular siete veces 19 y luego sumar cuarenta veces 19. Pero 7 por 19 se puede calcular como 7 por 9 y sumarle 7 por 10. De esta forma se obtiene que:
7 × 19 = 7 × 9 + 7 × 10 = 63 + 70 = 133. (1)
Por otro lado, cuarenta veces 19 no es otra cosa que multiplicar 19 primero por cuatro y luego por 10. Sin embargo, como multiplicar por diez implica añadir un cero, resulta que:
4 × 19 = 4 × 9 + 4 × 10 = 36 + 40 = 76
y por lo tanto,
40 × 19 = 760. (2)
Al sustituir las operaciones de (1) y (2) tenemos que:
19 × 47 = 19 × 40 + 19 × 7 = 760 + 133
y esto se resuelve con el procedimiento de la adición: 760 + 133 = 893. Si procedemos a multiplicar siguiendo el esquema aprendido no hacemos otra cosa que seguir esta lógica.
Lo principal es que no importa cuán grandes sean los números, el procedimiento siempre funciona —aunque a veces sea muy tedioso y prefiramos tomar una calculadora de bolsillo para resolverlo. Aunque estas herramientas nos son muy útiles, también es relevante comprender que el mecanismo que gobierna el procedimiento aprendido es una absoluta necesidad. En el fondo de cada multiplicación siempre están las tablas de multiplicar del uno hasta el nueve. Desde esta perspectiva, no hay nada de sorprendente en el hecho de que todos los niños del planeta tienen que aprenderse las tablas de multiplicar de igual manera.
Si denotáramos nuestros números como los romanos tendríamos serios problemas para hacer cálculos. Ahora entendemos por qué se dice que los progresos científicos de los romanos fueron muy limitados, precisamente porque no usaban un buen sistema de notación.
