En Babilonia y Egipto se desarrolló el conocimiento para construir edificaciones y trazar ciudades, el cual perdura hasta nuestros días. Uno de los puntos básicos de esta tecnología es poder trazar ángulos rectos, pues da lugar a formas racionales de dividir los espacios, y para lograrlo se usaba el siguiente método. Al trazar un triángulo cuyos lados miden 3, 4 y 5 unidades de longitud —no importa si son metros, pies o una vara cualquiera—, se forma un ángulo recto entre los lados que miden 3 y 4. Este mismo método lo usan en la actualidad nuestros albañiles para encontrar la "escuadra" con más precisión de lo que da una pequeña regleta: toman un "reventón" —así le llaman a los hilos con que se guían para la construcciónd— de 12 metros (3 + 4 + 5 = 12), lo tensan en los puntos correspondientes y ahí, entre los lados de 3 y 4 unidades, obtienen su esquina perfecta.
Esta manera de trazar triángulos rectángulos se manejaba como conocimiento empírico, es decir, práctico y corroborado por la experiencia, hasta que los griegos exhibieron lo que hacía tan especial a la terna de números 3, 4 y 5. Para esto, deben haberse preguntado algo como: ¿habrá otras ternas de números con la propiedad de formar ángulos rectos?, ¿qué las distingue?
La respuesta a la pregunta sobre qué ternas forman ángulos rectos es sorprendente: tiene que ver con áreas. Si nos fijamos en los tres cuadrados cuyos lados son los números dados, la suma de las áreas de los dos cuadrados chicos tiene que ser igual al área del cuadrado grande. Cualquier albañil babilonio estará de acuerdo en que con 25 losetas cuadradas se pueden cubrir un cuadrado de 5 por 5, o bien uno de 3 por 3 y uno de 4 por 4 . Con la notación de nuestros días, podríamos escribir lo anterior como:
32 + 42 = 9 + 16 = 25 = 52 .
Se sabe que los babilonios ya habían observado esta relación numérica y, además, de que conocían otros ejemplos. Pero que esto no fuera una casualidad, sino la razón profunda de que el método para trazar ángulos rectos funcionara, es un salto a otro nivel de entendimiento. Una pregunta abstracta, intrínsecamente matemática, sobre la relación entre una terna de números ( 3, 4 y 5) y un hecho geométrico, el que con ellos se construye un ángulo recto, da lugar al célebre teorema de Pitágoras, uno de los primeros en su género y un logro de la humanidad equiparable al descubrimiento del fuego o de la rueda. El descubrimiento de la primera "verdad" general y no trivial, como que dos más dos son cuatro, que no depende de la fe o la experiencia, sino que es producto del razonamiento puro. Una verdad que tiene razón de ser más allá de la cultura o idiosincrasia desde la cual se le contemple. Una verdad que, además, rige a la realidad que nos circunda y sugiere que dicha realidad puede comprenderse por medio de la razón.
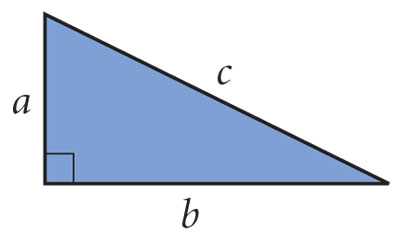
El teorema de Pitágoras dice que las ternas de números a, b, c , ordenadas de manera creciente y que corresponden a las longitudes de los lados de triángulos rectángulos son las que cumplen la relación:
a2 + b2 = c2. (1)
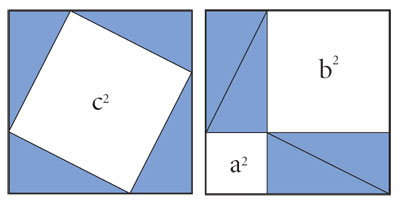
Pitágoras lo enunció en términos de áreas y para nuestros propósitos no es relevante cuál fue su motivación o argumentación original, lo importante es que dio el gran salto a un enunciado general y demostrable. Una prueba del teorema se obtiene al colocar, de dos maneras diferentes, cuatro triángulos rectángulos con catetos a y b en un cuadrado de lado a + b , como en la figura 1.28. Lo que dejan de cubrir estos cuatro triángulos en una de ellas son dos cuadrados de lados a y b , con área total a2 + b2 ; y, en la otra, lo que no cubren es un cuadrado cuyo lado es la hipotenusa c.
De la ecuación (1), al considerar que la terna 3, 4, 5 la satisface, surgen dos preguntas interesantes. La primera es si habrá otras ternas de números naturales que la cumplan, además de las obvias que son múltiplos de la original como por ejemplo 6, 8, 10 , es decir, si hay otros triángulos rectángulos cuyos lados sean enteros. La respuesta es que sí. Por ejemplo, la siguiente "terna pitagórica" primitiva, que quiere decir que no es múltiplo de otra, es 5, 12, 13 . La escuela que se formó alrededor de Pitágoras y continuó los trabajos después de su muerte, alrededor del año 507 a.C., obtuvo familias infinitas de estas ternas. Demostraron, por ejemplo, que cualquier número impar es parte de una de ellas. Sin embargo, no fue hasta el siglo XIII que Fibonacci encontró un método para listar todas las ternas pitagóricas.
La segunda pregunta que surge de la ecuación (1) es más general y ya no tiene una connotación geométrica tan evidente. No obstante, tiene una historia que ilustra el punto remarcado en esta sección. Si cambiamos el exponente 2 por uno más grande 3, 4, 5, 6, . . . , que podemos denotar por n , se obtiene la ecuación
an + bn = cn. (2)
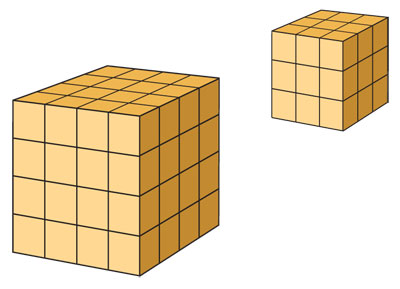
Para n = 3, esta ecuación tiene aun un significado geométrico. ¿Se puede partir un cubo formado por cubitos unitarios en dos cubos también formados por cubitos unitarios? Es una pregunta que nos invita a buscar una solución: ¿ 23 + 33 será igual a 43 ? No, porque 8 + 27 = 35 es diferente de 64 . Pero quizás haya otros números para los cuales sí es cierto... o quizá no. O bien podemos encontrar una terna de números y resolvemos la pregunta, o bien habrá que demostrar que esto es imposible.
La pregunta más general puede plantearse así: ¿la ecuación an + bn = cn tiene soluciones enteras?, es decir, ¿existen números a, b, c enteros tales que an + bn= cn? Este problema se atribuye a Pierre de Fermat en el siglo XV, aunque es muy probable que se hubiera planteado antes dado lo natural que es.
Cuenta la leyenda que Fermat escribió en el margen de un libro que había encontrado una demostración muy elegante de que sólo para n = 2 había soluciones enteras, resultado que se refiere a las ternas pitagóricas. Dicha demostración "elegante" nunca apareció, por lo que se hizo famoso el problema como el "Teorema de Fermat". En realidad no era —todavía— un teorema sino una conjetura: la intuición profunda de algo que debe ser cierto, acompañada de fuertes indicios de que es cierto, pero que carece de una demostración. Fermat sí dejó una demostración para el caso n = 4, es decir, que para n = 4 la ecuación (2) no tiene ninguna solución entera. A lo largo de los siglos siguientes se demostró la imposibilidad para otros casos como n = 3, 5 y 7. También se demostró para algunas familias infinitas de potencias n. Cada paso añadía fundamento y glamour a la conjetura.
No fue sino hasta 1995 cuando se concluyó la demostración del teorema de Fermat. El matemático inglés Andrew Wiles dio los pasos finales y es a quien se atribuye la demostración. Quedará para los siglos venideros como el "teorema de Fermat-Wiles". Pero, como decía Newton, para ver lejos, Wiles se paró sobre los hombros de gigantes. En este caso, los gigantes son innumerables pues se desarrollaron áreas completas de las matemáticas, como la teoría algebraica de los números y la geometría algebraica, cuyas ideas y conceptos son la base de la demostración. Éste es un ejemplo célebre de un problema intrínsecamente matemático, sencillo de plantear, que fue semillero de grandes desarrollos. Ejemplo claro de cómo las propias matemáticas generan preguntas que dan lugar a nuevas matemáticas.