Como se explica en la introducción a la materia, este libro se divide en tres partes que corresponden a las principales fuentes de motivación para la creación matemática: la actividad humana, la naturaleza y las propias matemáticas. El propósito de este primer capítulo es ilustrar, con ejemplos sencillos, dichas fuentes de motivación matemática.
Sin embargo, es conveniente aclarar que hay una fuente de creación matemática que antecede a las otras y sin la cual serían estériles: la irresistible atracción del ser humano por los retos de todo tipo, en especial, los intelectuales. Esta atracción no se limita a un grupo especial o selecto de personas, como los matemáticos, sino que se puede reconocer en cualquier persona, por ejemplo, cuando en un café o en el metro se resuelve como entretenimiento uno de los sudokus impresos a diario en los periódicos. ¿Qué es lo que lleva a una persona a intentar, durante largas horas, resolver estos retos? ¿Qué gana con ello? Quienes nunca lo han hecho les puede parecer extraño, pero lo único que se obtiene es la satisfacción de haberlo resuelto, de lograr algo con la mente.
Hace mucho tiempo que los periódicos imprimen juegos de entretenimiento o desafíos mentales, como los crucigramas. Unos cien años atrás estaban de moda los problemas de ajedrez, hace unos decenios el cubo de Rubik y ahora los sudokus. Los periódicos están al corriente de que a muchos de sus lectores les encantan estos juegos y de que hay quienes los compran sólo por ellos, por consiguiente, siempre tienen secciones que los contienen.
Antes de los sudokus o de otros desafíos ya mencionados, muchas personas dedicaban su tiempo libre a encontrar cuadrados mágicos, que son arreglos de números en los que se obtiene la misma suma en cada fila y columna. Podemos ver un ejemplo en el grabado Melancolía de Alberto Durero, arriba y a la derecha, bajo la campana.
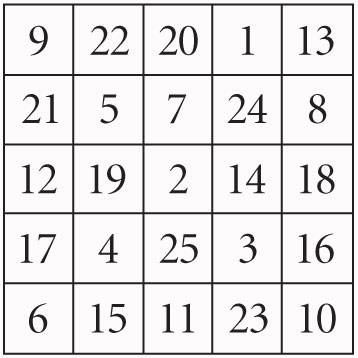
La figura 1.4 es un cuadrado mágico más grande que el del cuadro de Durero, donde la suma de cada fila y columna es de 65.

Los cuadrados mágicos eran conocidos desde el año 650 a.C. por los matemáticos chinos y alrededor del siglo VII d.C. por los árabes. Aparecen también en las culturas de India y Persia y, en cada una de ellas, se les atribuyen distintos poderes, como el de atraer la suerte.
Podemos construir fácilmente un cuadrado mágico de tamaño tres por tres. Primero determinamos cuál debe ser la suma de los números en cada fila y columna. Si usamos los números del 1 al 9 la suma es:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
Como esta suma debe distribuirse en tres renglones, cada uno debe sumar 15. Si en alguna celda ponemos el número más grande, o sea el 9, debemos sumarle solamente 6 en las otras dos celdas de su misma fila y su misma columna. La única forma de sumar 6 con los números restantes son: 1 + 5 y 2 + 4, ya que 3 + 3 repite un número. Usamos estas dos combinaciones para llenar la fila y la columna donde ya habíamos colocado el 9, así que el actual estado de nuestro cuadrado mágico es como sigue:
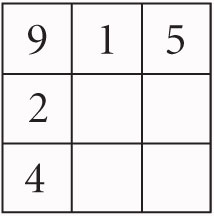
En las cuatro celdas restantes debemos colocar los cuatro números que faltan: 3, 6, 7 y 8. Buscaremos ahora la ubicación del número 7. No puede estar en la misma fila que el 4 dado que 4 + 7 = 11 y nos faltarían justo otros 4 para alcanzar la suma 15. De la misma manera, no puede estar en la columna del 1, pues faltarían 7. Por ello, sólo queda un lugar para el 7: debe estar en la columna del 5 y la fila del 2. Ahora, es fácil terminar de rellenar el cuadrado mágico. Se deja este ejercicio para que el lector lo termine.
¿Qué pasos seguimos para construir el cuadrado mágico de 3 por 3? No se probaron muchas distribuciones para ver, si de casualidad, una funcionaba. Tampoco seguimos una estrategia ordenada para evaluar todos los posibles arreglos sin repetir uno, hasta encontrar el que buscábamos. Simplemente, empleamos el razonamiento lógico, ningún otro procedimiento puede llevarnos al resultado. Cuando logramos resolver un problema por deducción lógica, sentimos la misma satisfacción que un niño al poner la última pieza de un rompecabezas.
Usemos este cuadrado mágico para formar un sudoku: si intercambiamos filas o columnas obtenemos otros cuadrados mágicos de 3 por 3 que podemos acomodar en el tablero, por ejemplo, de la siguiente manera:

Este sudoku terminado consiste en nueve cuadrados mágicos; si además elegimos, por ejemplo, la esquina superior izquierda de cada bloque, obtenemos un arreglo de tres por tres números que, a su vez, forman otro cuadrado mágico. Lo mismo ocurre para cualquier otra celda que elijamos en cada bloque.
Se pueden hacer cuadrados mágicos de todos los tamaños: tres por tres, cuatro por cuatro, cien por cien o tres millones por tres millones. También de uno por uno, que consiste en una única celda, pero como es el ejemplo más sencillo, no presenta mucho interés. No obstante, hay un tamaño imposible para los cuadrados mágicos. ¿Cuál es? Dejamos este reto al lector.
Los cuadrados mágicos no tuvieron mayor trascendencia en la historia ni en la ciencia. En un principio, quizá se emplearon con la esperanza de encontrar algo verdaderamente mágico pero, con el tiempo, se convirtieron en un simple pasatiempo. Sin embargo, cautivaron por igual a hombres y mujeres de distintas épocas y culturas, al evidenciar la fascinación de la humanidad por los retos intelectuales.
Si bien no todas las personas responden a estos desafíos, hay algo en la naturaleza humana que impulsa a plantearse problemas e intentar resolverlos. Este impulso es característico de la actividad matemática, aunque las matemáticas son mucho más que eso según veremos en las siguientes secciones.