Las termoeléctricas modernas son descendientes lejanas de los primeros motores térmicos europeos del siglo XVII. Esos motores transformaban calor en trabajo, quemando carbón. La figura 16 muestra una representación del motor de Newcomen (1663-1729), inventor inglés, quien se dedicó a resolver el problema de cómo efectuar trabajo mecánico a partir de la combustión del carbón para aplicarlo en la extracción del mismo y del agua de las minas, así como para utilizarlo en las múltiples tareas de las fábricas de hilados, tejidos, etcétera.
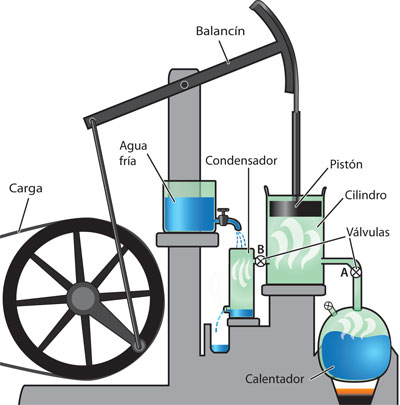
El funcionamiento del motor de Newcomen es el siguiente: si las válvulas B y C están cerradas y se abre la válvula A, entrará vapor caliente de la caldera. Éste empuja al pistón hacia arriba, moviendo el balancín para subir una carga de agua o de carbón desde el fondo de la mina. Cuando el pistón se encuentra en la parte superior del cilindro, se cierra la válvula A y se abre la C, vertiendo agua fría sobre el cilindro y el pistón. Este enfriamiento condensa al vapor del interior del cilindro, disminuyendo su presión por debajo de la presión atmosférica, haciendo que el pistón se mueva hacia abajo. Se abre la válvula B y el vapor residual escapa al exterior. El ciclo comienza de nuevo al abrirse la válvula A, para dejar entrar vapor otra vez, estando las válvulas B y C cerradas, y así sucesivamente (p. 443).
Antiguamente la eficiencia del motor de Newcomen no pasaba de 1 a 2% por varias razones: el ajuste entre el pistón y las paredes del cilindro era tan deficiente que una moneda podía caber en el espacio intermedio. Pero fue Watt quien descubrió la causa principal de la ineficiencia. Él estudió un modelo a escala del motor de Newcomen y descubrió que los calentamientos y enfriamientos sucesivos del cilindro y el émbolo podían evitarse separando la operación de condensación, evitando así la necesidad de que en una misma parte del motor se efectuaran las dos operaciones de calentamiento y enfriamiento. Su propuesta se esquematiza en la figura 17 (p. 444).

Con la válvula B cerrada se abre la A; el vapor caliente entra al cilindro, lo que ocasiona que el émbolo se mueva hacia arriba, empujando al balancín para elevar la carga o realizar otras tareas. Después se cierra la válvula A y se abre la B, dejando salir vapor al condensador. Enseguida se abre de nuevo la válvula A, cerrando la B y el ciclo se repite. Watt, con su motor, fue capaz de elevar la eficiencia del motor de Newcomen hasta un valor del 7%, es decir, un factor superior a 3. El francés Sadi Carnot, gran teórico de los motores térmicos, en 1824, indicó a propósito de la importancia de su desarrollo:
El servicio más relevante que el motor térmico ha hecho en Inglaterra es, sin duda, el de haber reanimado la explotación de sus minas de hulla, que había disminuido y que amenazaba por extinguirse completamente a causa de la dificultad siempre creciente para el desagüe y la extracción del combustible (la extracción de hulla se multiplicó por diez, sucediendo algo semejante con otros minerales, tanto en Europa como en el Nuevo Mundo). Se deben colocar en segundo lugar los servicios prestados a la fabricación del hierro, tanto por la hulla que se ofrecía en abundancia como sustituto de la madera cuando ésta empezaba a agotarse, como por las potentes máquinas de toda clase, cuyo uso permitió o facilitó el empleo del motor térmico.
Más adelante, dice Carnot:
Quitar hoy a Inglaterra sus motores térmicos sería arrebatarle la hulla y el hierro al mismo tiempo; esto equivaldría a agotar todas sus fuentes de riqueza y arruinar todos sus medios de prosperidad; eso significaría aniquilar esta potencia colosal.
En aquellos tiempos, uno de los problemas era que la extracción del carbón de las minas se tenía que hacer desde el subsuelo, pues para entonces ya se había agotado el carbón superficial, con el agravante de que la perforación penetraba las capas freáticas y las minas se inundaban. Era necesario extraer el agua y el carbón simultáneamente, con rapidez suficiente; es decir, se necesitaba elevar desde el fondo de la mina (a una profundidad h) una cierta cantidad de agua de masa m, en un tiempo t, para permitir la extracción de carbón. Según lo expuesto en el capítulo de mecánica, se debería poder desarrollar una potencia:
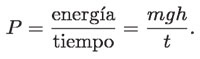
Para tener una idea cuantitativa, se tenía que elevar una tonelada de agua desde una profundidad de 20 metros en un minuto. La potencia mínima que los animales o el motor tendrían que desarrollar sería de:
P = (1 000 kg × 9.8 m/s2 × 20 m)/60 s = 3 267 W.
Un aparato que puede desarrollar una potencia comparable sería un automóvil de unos 100 caballos de potencia (HP). La conversión de HP a watt es de:
1 HP = 746 W.
Por lo tanto, la potencia en watt del motor de un automóvil de 100 HP es de
100 HP = 100 × 746 W = 7 460 W,
casi el doble de la potencia que se necesita en la tarea del desagüe.
El término "caballo de potencia" probablemente esté relacionado con una cláusula del contrato que Boulton y Watt hacían firmar a los clientes a quienes vendían los servicios de sus motores térmicos. Boulton se había asociado con Watt para vender lo que, según ellos, todos querían: "energía". Una parte medular del contrato decía lo siguiente:
Nuestra firma, Boulton y Watt, instalará la máquina, libre, gratis y por nada en su mina. La haremos funcionar durante los primeros cinco años y todo lo que pedimos a cambio es una tercera parte de la diferencia entre el costo del carbón para nuestra máquina y el costo del forraje para los caballos que tuviesen que realizar la misma cantidad de trabajo.
Lo que pedían Boulton y Watt era:
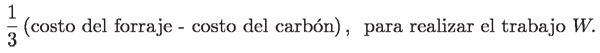
En el párrafo aparecen dos términos que requieren de una definición precisa, además de un procedimiento riguroso para medirlos con exactitud: el trabajo desarrollado por un caballo y el trabajo desarrollado por el motor térmico construido por la compañía, así como las cantidades de carbón y forraje consumidas cuando ambos trabajos son iguales. Mientras que la cantidad de carbón necesaria para elevar una cierta cantidad de agua (o de carbón) de una cierta profundidad podía calcularse mediante pruebas directas con el motor, no era tan fácil calcular para un caballo.
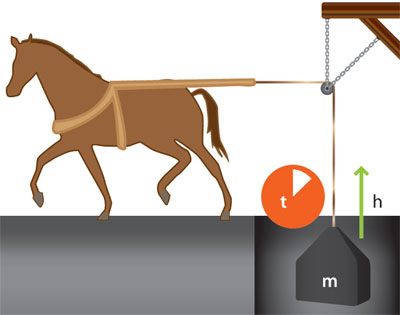
Watt realizó el siguiente experimento: ató una cuerda a un cuerpo de masa m, la introdujo en un pozo de profundidad h, hizo pasar la cuerda por una polea situada en la boca del pozo y luego la amarró al arnés de un caballo. Ajustó m, h y el tiempo de elevación para saber la potencia máxima (Pmáx) a la que el animal podía trabajar durante un cierto tiempo t sin cansarse, llegando así a que la Pmáx calculada adquirió un valor cercano al que conocemos ahora de 746 W.
Quienes vendían y compraban tenían que comprender los términos de la transacción; por eso los conceptos de cantidad de trabajo, potencia y energía (ahora comunes en la física) fueron inventados para la aplicación de los motores térmicos en la sociedad.
Por otro lado, un concepto fundamental necesario para definir la operación de un motor térmico es su eficiencia (representada por la letra griega η, eta). La eficiencia es el cociente del trabajo obtenido por el motor entre la cantidad del calor que recibe de la caldera.
La operación del motor de Newcomen satisfizo desde el principio a sus usuarios. Sin embargo, en la medida en que el costo del carbón aumentaba, se hacía necesario obtener más trabajo con la misma cantidad de carbón, o sea, era necesario aumentar la eficiencia η. Por eso, el desarrollo de motores térmicos continuó y James Watt (1736-1819) produjo una revolución en su funcionamiento.
Sadi Carnot (1796-1832), estudiando los motores térmicos de su época, descubrió los tres elementos universales del motor térmico: la caldera, el ciclo de la sustancia que trabaja y el condensador. Se propuso estudiar científicamente los motores térmicos, porque eran parte vital de la actividad económica y productiva de las naciones altamente industrializadas, en particular Inglaterra. Carnot observó que el aumento de la eficiencia, con las sucesivas modificaciones a los motores térmicos, era cada vez menor. Watt había obtenido al principio un salto espectacular de 300% con respecto a la eficiencia del motor de Newcomen; pero en los cambios subsiguientes la eficiencia parecía tener un límite del cual no podría pasarse, independientemente de que se mejorara el diseño o la sustancia con la que trabajara el motor. Carnot se preguntó si la eficiencia podía aumentarse indefinidamente hasta 100%, en cuyo caso todo el calor de la caldera se convertiría en trabajo, ya fuera por el cambio de diseño, la naturaleza de la sustancia con que trabajara o cualquier otro factor.
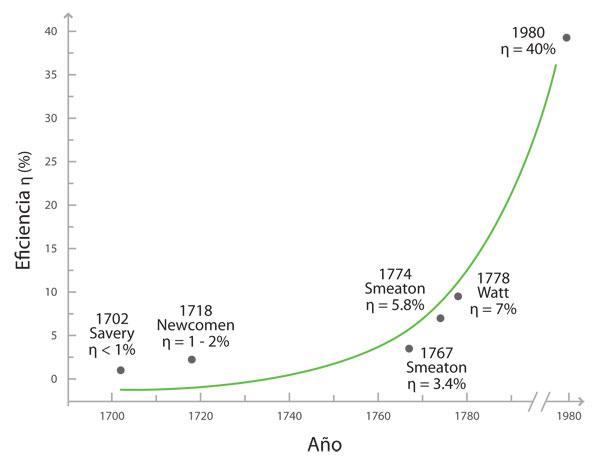
La pregunta tenía sentido porque, como se puede observar en la figura 19, el límite de η quedaba lejos del valor 1, es decir, de 100 por ciento.
En la figura 20 (p. 448) se muestra un esquema del motor térmico universal.
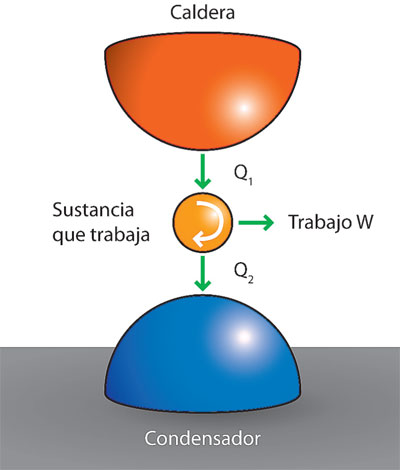
En primer lugar, la caldera donde se quema el carbón y se genera el calor Q1 que actúa sobre la "sustancia que trabaja" (el vapor de agua que ingresa al cilindro); en segundo lugar, la sustancia que trabaja en el cilindro, que lo hace en ciclos, y, por último, se tiene el condensador, que recibe la energía disipada por calor Q2. Con estos elementos, Sadi Carnot logró establecer que:
1] En el motor térmico era tan importante el condensador (a baja temperatura) como la caldera (a alta temperatura) para poder desarrollar trabajo, porque preveía que si el ambiente estuviera todo a la temperatura de la caldera, el calor no podría "fluir", pues no habría la posibilidad de "pasar" a un lugar con menor temperatura. En otras palabras, Carnot utilizó el modelo "sustancialista", el cual supone que el calor es similar a un líquido que necesita pasar de un nivel superior a uno inferior para moverse, al igual que el agua en una cascada.
2] El máximo trabajo que se puede obtener de Q1 es mediante la utilización de un motor que opere reversiblemente, es decir, sin que haya fricción entre sus partes y que opere muy lentamente. Este importante enunciado es el ahora conocido teorema de Carnot, el que también puede enunciarse en términos de la eficiencia, es decir: Ningún motor térmico funcionando entre una caldera y un condensador fijos puede tener eficiencia mayor que la de un motor reversible funcionando entre la misma caldera y el mismo condensador.
3] El trabajo debía depender de la diferencia de temperatura o "caída de temperatura" (t1 – t2) entre la caldera a t1 y el condensador a t2.
4] El trabajo máximo no solamente depende de la "caída" en temperatura (t1 – t2), sino que aumenta al disminuir la temperatura t1 de la caldera; es decir, el calor Q1 produce más trabajo en la caída de 50 °C a 10 °C, que de 90 °C a 50 °C, aunque en ambos casos la diferencia de temperaturas sea de 40 °C.
En la demostración de estos resultados, Sadi Carnot se guió por la analogía hidráulica que años antes su padre, Lázaro Carnot, había establecido con un teorema: Los motores hidráulicos, es decir, las ruedas de agua verticales de máxima potencia, son las que funcionan reversiblemente.
La rueda de agua funciona reversiblemente si una masa m de agua, que se recibe en un cajón de la rueda a la altura h1, baja al rotar la rueda a la altura h2 y regresa de nuevo a la altura inicial. Cuando la masa de agua se encuentra a la altura h, la conservación de energía nos dice que:
Energía de rotación de la masa m + Energía de rotación de la rueda + Energía perdida por fricción + mgh = mgh1.
Llamemos ER a la suma de las energías de rotación de la masa m y la rueda, y EF a la energía perdida por fricción, por ejemplo en el eje de rotación de la rueda. Tenemos, por la conservación de la energía total:
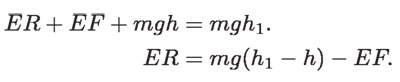
Si no hay fricción en la rueda, que es reversible, es decir, EF = 0, entonces:
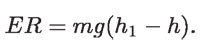
O sea, la energía de rotación del sistema (rueda y masa de agua m) aumenta conforme disminuye h, es decir, conforme m baja al rotar la rueda. El valor mínimo de h al que m puede bajar, que es h2, corresponde al valor máximo de ER, que denotaremos por ERmáx, por lo que:
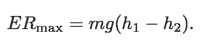
Si la rueda opera sin fricción y no se pierde agua durante todo el trayecto, es decir, si la rueda opera reversiblemente, la masa m seguirá subiendo después de alcanzar el punto más bajo de la rueda, hasta llegar nuevamente a la altura superior h1, de la cual partió. En este punto otra vez ER = 0. Si hubiera fricción en alguna parte, por ejemplo en el eje de giro de la rueda o se presentara una fuerte corriente de aire, la rueda se detendría a una altura h menor que h1; de hecho, hasta podría ser que m no llegara hasta abajo.

Ahora bien, si se quiere hacer funcionar algún otro dispositivo técnico usando la rueda en rotación, el trabajo máximo que se puede obtener será igual al valor máximo de la energía de rotación. En otras palabras, el máximo trabajo que puede realizar la rueda, llamémosle Wmáx, será el que la deja quieta, con la masa m en la posición más baja h2. Por lo tanto:
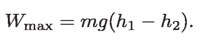
Esta ecuación nos lleva a que Wmáx depende de la "caída" de altura (h1 – h2).
Los motores se caracterizan por su eficiencia, que es el trabajo que pueden desarrollar en relación con la energía suministrada, y está definida como:

La eficiencia es máxima cuando para una inversión de energía potencial de la masa m a la altura h1, se obtiene el trabajo máximo, que es el desarrollado por la rueda de agua reversible:
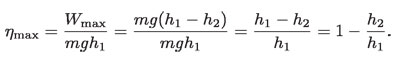
El máximo trabajo también se puede expresar en términos de la máxima eficiencia:
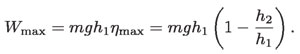
Una propiedad interesante de Wmáx es que aumenta al disminuir h1. Es decir, el máximo trabajo es mayor a pequeña altura que a gran altura, aunque la caída (h1- h2) sea la misma.
Un motor térmico funciona reversiblemente si los intercambios de energía de la sustancia que trabaja con la caldera y el condensador son muy lentos, sin fricción y sin disipación, de tal manera que al invertir las "entradas" y "salidas" de energía en el motor se invierten exactamente.
El motor reversible funcionando al revés es un refrigerador; en la rueda hidráulica correspondería a la bomba hidráulica que transporta agua del nivel inferior al superior, para lo cual habría que realizar trabajo sobre la bomba. En un refrigerador, de manera semejante, también hay que invertir trabajo (eléctrico) para disminuir la energía interna y, por lo tanto, la temperatura de su interior (figura 21).
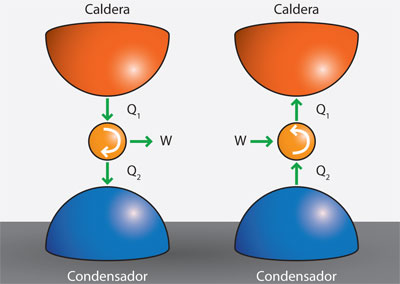
Sadi Carnot, de acuerdo con la analogía hidráulica, establece un teorema semejante al de su padre:
Ningún motor térmico funcionando entre una caldera y un condensador fijos puede tener eficiencia mayor que un motor reversible operando entre la misma caldera y el mismo condensador.
Las condiciones de operación cíclicas de un motor térmico reversible son análogas a las de operación de una rueda hidráulica, siguiendo el ciclo de Lázaro Carnot. Es decir, el ciclo térmico de Sadi Carnot está compuesto de cuatro pasos reversibles:
1] La sustancia que trabaja dentro del cilindro recibe una cantidad de energía por calor Q1 de la caldera, sin fricción ni disipación. Esto significa que Q1 debe aumentar la energía de la sustancia muy lentamente, siempre muy cerca del equilibrio, a la temperatura constante de la caldera T1. Esto corresponde, en la rueda hidráulica, a que el agua se recibe en el cajón con velocidad relativa cero, a la altura h1.
Si el proceso no fuera isotérmico, sino que se realizara a una diferencia finita de temperatura, sería semejante a que se recibiera el agua a una altura superior a h1, produciéndose rebotes y pérdidas, violándose las condiciones de reversibilidad. El aumento de la energía interna de la sustancia que trabaja provoca en ella una expansión isotérmica, denotada por el paso de A a B en la figura 22.
2] La expansión de B a C se efectúa adiabáticamente, es decir, sin cambios por calor (Q = 0) en la energía interna de la sustancia, que en la rueda corresponde a la bajada del agua sin pérdidas de líquido.
3] En la etapa de compresión de C a D la sustancia pierde energía por calor Q2 y la cede al condensador, de manera isotérmica.
4] Finalmente, la sustancia que realiza el trabajo regresa a la posición inicial, por un paso semejante al 2, pero ahora de compresión.
Sadi Carnot había notado que la analogía del motor térmico con el motor hidráulico no es exacta, porque Q1 ≠ Q2, y el trabajo desarrollado W = Q1 – Q2 es distinto de cero. En el motor hidráulico, en cambio, la cantidad de líquido que cae se conserva.
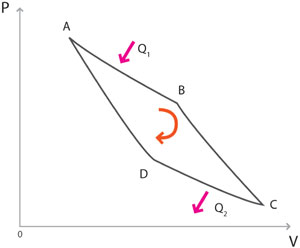
El ciclo de Sadi Carnot se compone de dos isotermas y dos adiabáticas reversibles. Para mayor comprensión, en la figura 23 se dibuja un gas encerrado en un cilindro con un pistón, en contacto diatérmico con una caldera, recibiendo energía por calor isotérmicamente.
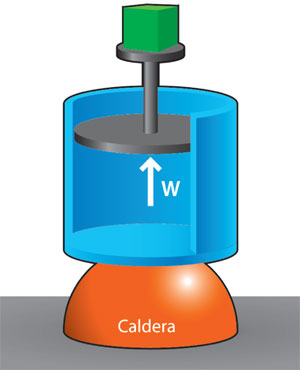
La eficiencia de un motor térmico será la máxima y, por analogía con la rueda reversible en que la máxima eficiencia es 1 – h2 / h1, tendrá el valor:
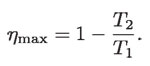
Como:
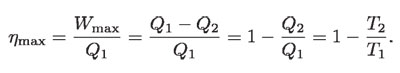
se tiene que el máximo trabajo térmico vale:
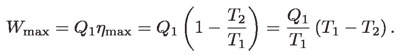
Es decir, se cumple que el trabajo máximo depende de la "caída", o "diferencia" de temperaturas (T1 – T2), pero aumenta conforme disminuye T1, tal y como había anticipado Sadi Carnot. Esto mismo sucede en un motor hidráulico.
De la expresión para la máxima eficiencia térmica:
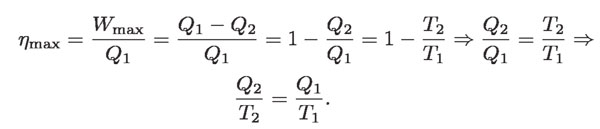
Al cambio de estado físico, calculado por el cociente Q/T, se le llama cambio de entropía de la caldera o del condensador. Si la entropía se denota por S, y su cambio por ΔS, la igualdad
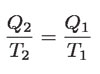
implica que
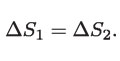
En esta igualdad los valores de los cambios de entropía son absolutos, es decir, positivos. Pero si tomamos en cuenta que Q1 es en realidad negativo, porque se extrae energía de la caldera, se tiene que el cambio de entropía de ésta será también negativo:
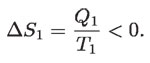
Por el contrario, el cambio de entropía del condensador (Q2 > 0) es positivo:
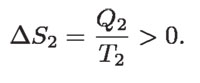
Por lo tanto, en vez de ΔS1 = ΔS2, que se refiere a valores absolutos, se debe tener:
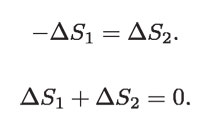
Como la sustancia que trabaja cambia cíclicamente de estado como consecuencia de los intercambios energéticos con la caldera y el condensador, su cambio de entropía es cero. Así que, si sumamos todos los cambios de entropía involucrados en la operación de un motor reversible, se concluye que:
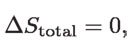
si los procesos en el motor son reversibles.
Si, por el contrario, los intercambios energéticos entre la sustancia que trabaja, la caldera y el condensador son irreversibles, entonces la cantidad ΔQ/T no se conserva, sino que en valor absoluto será mayor la del condensador que la de la caldera.
Supongamos ahora un motor irreversible que procesa calor Q1 de la caldera y Q2 del condensador. El teorema de Carnot afirma que su eficiencia será menor que la de un motor reversible funcionando entre dicha caldera y condensador; por lo tanto:
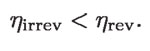
Es decir:
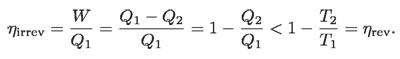
De aquí se deduce que:
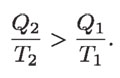
En términos de cambios de entropías y si, como antes, se toman en cuenta sus signos:
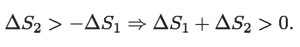
El cambio de entropía de la sustancia que trabaja sigue siendo nulo porque trabaja en ciclos completos. En consecuencia, es cierto ahora que:
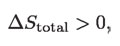
si los procesos en el motor son irreversibles.
Los dos resultados anteriores, que sólo se refieren a la operación de motores térmicos, se pueden expresar de otra manera. Para esto se define el universo termodinámico como el conjunto de objetos que participan en un proceso; en el caso del motor térmico, el universo está compuesto de la sustancia que trabaja, la caldera y el condensador.
Principio del incremento de la entropía: El cambio de entropía del universo termodinámico es positivo siempre que ocurre un proceso irreversible en su interior.
Si el proceso es reversible, entonces la entropía del universo permanece constante y no cambia. Ahora bien, es posible demostrar que el principio del incremento de la entropía es válido para cualquier tipo de proceso irreversible que ocurre en el interior del universo termodinámico, y no sólo para procesos involucrados en la operación de motores térmicos.
Una característica de todos los procesos que ocurren en el universo termodinámico es que se dan porque existe un desequilibrio, ya sea entre un objeto y otros, o en el interior del objeto. En el motor térmico, el desequilibrio se da entre la caldera y el condensador.
Los objetos evolucionan entonces hacia el equilibrio, de manera irreversible, de tal modo que la entropía del universo siempre crece. Una vez que este proceso hacia el equilibrio termina, se llega al reposo, que es el estado en que la entropía del universo llega a su valor máximo. El principio del incremento de la entropía marca así una dirección, que los procesos hacia el equilibrio deben seguir, es decir, hacia el estado del universo en que la entropía aumenta. Se dice también que el principio del incremento de la entropía fija un sentido en el tiempo, del pasado al futuro. Una consecuencia importante de lo expuesto es que los motores térmicos contaminan aun cuando funcionen reversiblemente, sin fricción ni disipación de energía.
El calor Q2 procesado necesariamente en el condensador, que generalmente es el ambiente, se traduce en contaminación; es decir, provoca un impacto ambiental que, ciertamente, es mínimo, pero no despreciable.
Si el motor es irreversible, tenemos que:
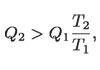
de modo que la contaminación térmica mínima es :
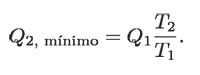
Esta energía por calor eleva la temperatura de algún cuerpo de agua (río, mar, etc.) o el aire, si la termoeléctrica cuenta con torres de enfriamiento. La contaminación térmica que genera suponiendo que Q2 es el calor de una termoeléctrica de 1 GW, que el condensador se enfría con el agua de un lago y que trabaja con una eficiencia de η = 0.36, entonces:
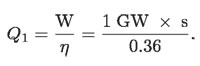
Por otro lado, la temperatura ambiente es de 300 K, mientras que la de la caldera es típicamente de 825 K, así que
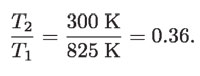
Entonces:
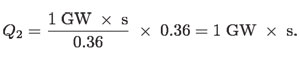
En un segundo, la termoeléctrica energiza el agua del lago con una energía de:
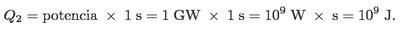
Si el lago tiene 10 km de diámetro y una profundidad promedio de 10 m, su volumen de agua es de:
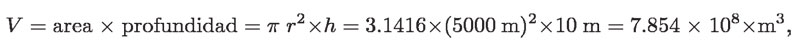
y la masa de agua es de:
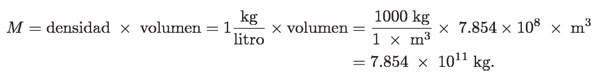
Por lo tanto, la energía de la termoeléctrica vertida por calor en un segundo en el lago eleva su temperatura en:
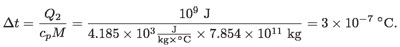
Se ha supuesto que la energía por calor es recibida de manera uniforme en un segundo por toda el agua del lago. El resultado anterior parece mostrar que el efecto térmico enel agua en un segundo es insignificante.
Sin embargo, la elevación de la temperatura en 5 °C es capaz de alterar severamente las condiciones de vida en el lago. Esta elevación se alcanza, según los cálculos simplificados anteriores, en apenas 190 días.
Obviamente, la contaminación térmica en los alrededores del desagüe del agua de enfriamiento que proviene del condensador, es mucho mayor de los 5 °C, por lo que su impacto es aún más intenso.
La contaminación térmica de las aguas provoca que disminuya la cantidad de oxígeno disuelto, pero que al mismo tiempo aumente la utilización de oxígeno por los organismos vivos del medio acuático, que se estratifiquen las aguas por diferencias en densidad y que se aceleren las reacciones químicas. Estos cambios hacen que disminuya la reproducción y la capacidad de supervivencia de los peces, que se limiten los patrones de migración, que se modifiquen los procesos que dependen de los ritmos biológicos, que se incremente la susceptibilidad a las enfermedades y el aumento desproporcionado de algunos organismos. Es decir, en apenas un año, un lago del tamaño considerado queda destruido. La única forma de no deteriorar térmica y químicamente el ambiente por causa de las termoeléctricas es evitando su uso. Los energéticos renovables son la alternativa. Esta contaminación inevitable es una consecuencia de la segunda ley de la termodinámica.