Si nos preguntamos: ¿por qué vuelan los aviones?, en la hidrodinámica también podremos encontrar respuesta, ya que el aire es también un fluido.
Para poder elevarse, un avión debe adquirir cierta velocidad en tierra.
En el siglo XVII el científico suizo Daniel Bernoulli (1700-1782), estudiando el flujo de agua en tubos cilíndricos rígidos, descubrió que la presión en las paredes laterales del tubo era menor cuando el agua se movía con mayor rapidez, que cuando el agua se movía más lentamente. Esto ocurría también con los gases. Sus descubrimientos los publicó en su obra Hidrodinámica, en 1738.
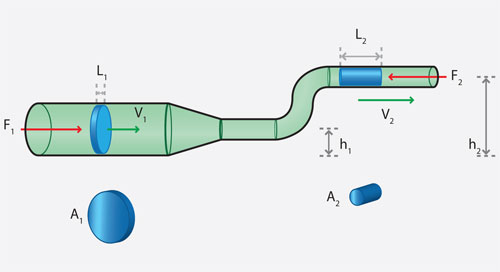
Para explicar la relación entre la velocidad del fluido y la presión que éste ejerce sobre las paredes del tubo en el que se desplaza, consideremos un flujo incompresible (puede ser de agua) constante, suave y sin turbulencias, en un tubo que cambia de diámetro y de altura. La región 1 es la parte ancha del tubo y la 2 es la parte delgada. Los volúmenes de agua son iguales en ambas partes (figura 17).
Sobre el volumen de la parte inferior del tubo se ejerce la fuerza F1 = P1 A1 (recuérdese que P = F/A), donde P1 es la presión en la región 1. Ahora, el trabajo realizado por esta fuerza al desplazar a este volumen es:
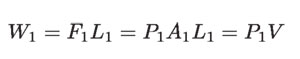
donde V, es el volumen.
De manera semejante, el trabajo realizado sobre el volumen de agua en la parte superior del tubo, en ese tiempo, es:
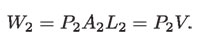
por conservación de la energía, ésta es la misma en ambas regiones:
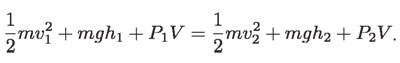
Entonces, como ρ = m/V (ρ es la densidad del agua), dividiendo cada término entre V, la expresión anterior se reduce a:
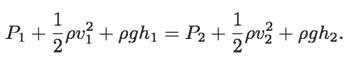
Ésta es la ecuación de Bernoulli para el flujo estacionario de fluidos incompresibles, como el agua. Esta ecuación establece que la suma de la presión, más la energía cinética por unidad de volumen, más la energía potencial por unidad de volumen, tiene el mismo valor en todos los puntos a lo largo del recorrido:
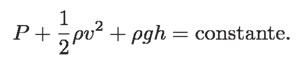
Para el caso en que el tubo es horizontal: h1 = h2 (figura 18), la ecuación de Bernoulli se reduce a:
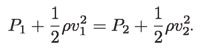
Esta expresión establece que cuando un fluido que se está desplazando dentro de un tubo pasa de una región 1 a otra región 2, con diferente diámetro, ocurre que si v2 es mayor que v1, entonces necesariamente P2 será menor que P1, y si v2 es menor que v1, entonces P2 será mayor que P1. Esto nos conduce al significado fenomenológico de la expresión: Para un fluido en movimiento, donde la velocidad se incrementa, la presión disminuye y viceversa.
El comportamiento de líquidos en movimiento se ha obtenido considerando que el fluido es incompresible, constante y sin turbulencias, a través de tubos cilíndricos rígidos. Sin embargo, se ha encontrado experimentalmente que funciona también, con muy buena aproximación, para todo tipo de fluidos (incluidos los compresibles como el aire) y a través de tubos no rígidos.
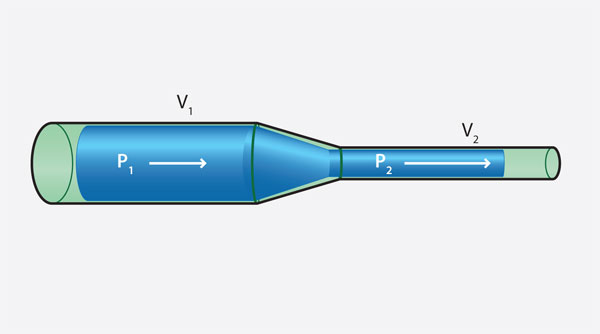
Una aplicación de la ecuación de Bernoulli se encuentra en el tubo de Venturi, estudiado por el físico italiano Giovanni Battista Venturi (1746-1822). Este tubo se ilustra en la figura 19 y con él se pueden medir velocidades de un fluido incompresible, como el agua. Así, puede determinarse la velocidad del flujo en la región 2, si se conoce la diferencia de presiones ΔP = P1 – P2 y las áreas transversales de ambas secciones (figura 19).
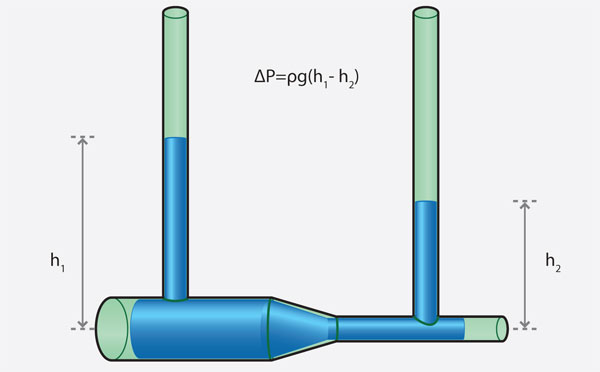
De acuerdo con las alturas del líquido en ambos tubos verticales, se tiene que, P1 > P2, y por lo tanto v1 < v2. Usando la ecuación de Bernoulli:

Además, de la ecuación de continuidad, A1v1 = A2v2, se tiene que v1 = A2v2/A1. Sustituyendo en la ecuación anterior, se obtiene:
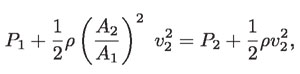
de donde:
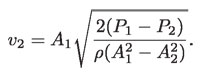
Así que, conociendo las secciones transversales del tubo, en las regiones 1 y 2, la diferencia de presiones (P1 – P2) y la densidad del fluido, se determina la velocidad del flujo en la región 2. Aplicando este resultado y la ecuación de continuidad, se puede conocer el valor de la velocidad de flujo en la región 1.
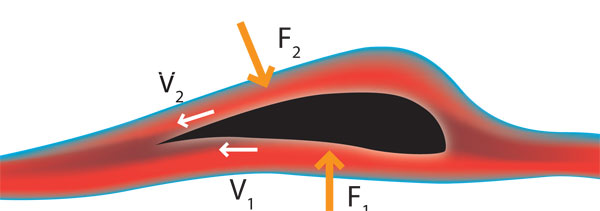
Es así que, ante la pregunta de por qué vuelan los aviones, se debe considerar la forma del ala, la cual ha de ser tal que mantenga un flujo uniforme del aire (figura 20).
El aire, en la región superior del ala, recorre una distancia mayor que la que recorre el aire en la parte inferior de ella, en el mismo tiempo. Por lo tanto, la velocidad del aire arriba del ala es mayor que por debajo de ella y, debido a esta diferencia de velocidades, la presión del aire en la parte superior del ala es menor que la presión del aire en la parte inferior.
Es así que la diferencia de presiones produce una fuerza neta hacia arriba, llamada fuerza de sustentación, la cual depende de la velocidad del avión y del ángulo entre el ala y la horizontal.
Ahora queda claro que para poder elevarse y mantenerse en vuelo, sobre los aviones debe actuar una fuerza de sustentación y, para ello, deben adquirir cierta velocidad.
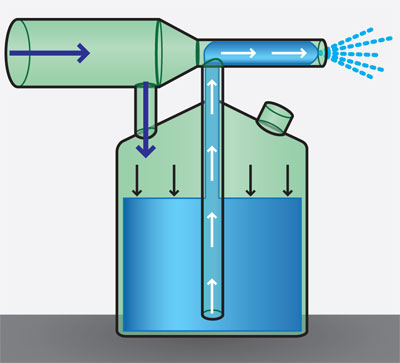
Otra aplicación de la ecuación de Bernoulli son los atomizadores y las pistolas de aire para pintar. En éstos, la corriente de aire pasa perpendicularmente por un extremo del tubo, inmerso en el líquido. El paso de aire a alta velocidad reduce la presión en la parte superior del tubo, y esta disminución hace subir al líquido hacia donde está pasando la corriente de aire y se dispersa formando una nube de pequeñas gotas. Desde luego, en este proceso físico, la presión atmosférica desempeña un papel importante para que el líquido suba por el tubo (figura 21).
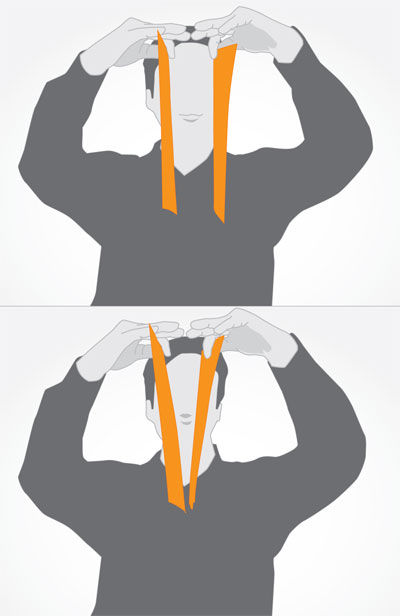
Un sencillo experimento que ejemplifica lo anterior es cuando, al sostener dos hojas de papel en posición vertical y paralelas frente a la boca de una persona y al soplar suavemente entre ellas, observamos que tienden a juntarse (figura 22).
La explicación es que al soplar suavemente entre las hojas se tiene entre ellas una zona de baja presión y, por ello, la presión atmosférica que afecta a las hojas por la parte externa las empuja, haciendo que se junten.