Cuando nos preguntamos: ¿por qué el agua de los ríos fluye con mayor velocidad donde el cauce es más angosto y lo hace lentamente donde el cauce es más ancho?, seguramente encontraremos respuesta gracias al estudio de los fluidos en movimiento, lo cual compete a la hidrodinámica.
En la hidrodinámica, un concepto importante es el de "gasto", el cual se define como el volumen "V" de un fluido que atraviesa una determinada superficie por unidad de tiempo y generalmente se denota con la letra Q. Su unidad es el metro cúbico sobre segundo "m3/s".
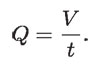
Con el concepto de gasto es posible cuantificar, por ejemplo, cuál es el volumen de agua que entra a la ciudad de México cada segundo, que es de varias decenas de metros cúbicos por segundo. O bien, la magnitud del gasto cardiaco en nuestro cuerpo, que en un hombre adulto en reposo es de aproximadamente cinco litros de sangre por minuto. Otro ejemplo es el gasto de gasolina de un coche que va en una carretera a 100 km/h, que es de aproximadamente 2 cm3/s.
Para estudiar el flujo de agua a través de tubos cilíndricos rígidos, considérese que éste es laminar y continuo; esto significa un flujo suave y sin turbulencias.
Supóngase agua fluyendo a lo largo de un tubo cilíndrico como el de la figura 16 (p. 399), en la que se observa que a partir de cierto punto, disminuye el diámetro del tubo. En la figura se muestra un mismo volumen de agua en dos regiones diferentes del tubo. Siendo igual el volumen, el que se encuentra en la región con menor área transversal tendrá mayor longitud. Si se denomina al volumen de la parte ancha del tubo como V1 y al volumen de la parte angosta como V2, se tendrá la siguiente igualdad V1 = V2, es decir, A1L1 = A2L2, de donde:
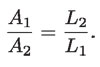
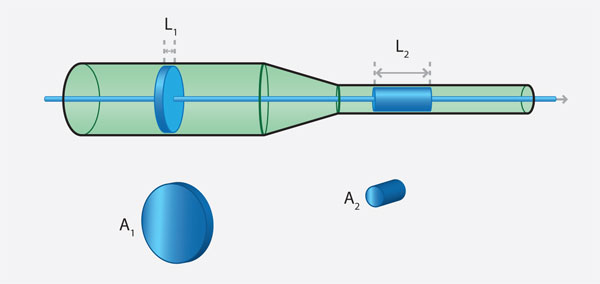
Si el gasto del agua que fluye por el tubo es constante y los volúmenes V1 y V2, son iguales, puede afirmarse que el tiempo que tarda el agua en recorrer el segmento L1 es igual al tiempo en que recorre L2. Como la velocidad es:
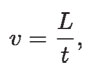
se puede escribir que:
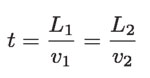
donde V1 y V2 son las velocidades con las que el agua se desplaza en ambas partes del tubo. De esta última expresión se obtiene que:
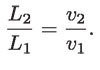
como:
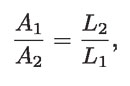
entonces:
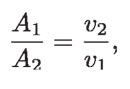
por lo tanto:
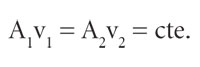
Esta ecuación es conocida como la ecuación de continuidad y representa la relación entre la velocidad de un fluido incompresible dentro de un tubo cilíndrico y el área transversal del mismo en dos puntos cualesquiera. Esto significa que el gasto es constante en cualquier parte del tubo. Si el área de una sección del tubo se reduce, la ecuación de continuidad predice que la velocidad necesariamente aumenta.
La respuesta a la pregunta de por qué el agua de los ríos fluye más rápidamente en las zonas donde el cauce se hace angosto y más lentamente en las zonas donde el cauce se hace ancho, se puede responder con base en que el gasto de agua en el río es constante y se puede aplicar la ecuación de continuidad.