Una lupa es una lente biconvexa usada en la vida cotidiana. Un microscopio también es conocido en amplios sectores por estudiantes, técnicos y profesionistas, quienes lo usan con regularidad. Es interesante conocer y comprender cómo estos instrumentos ópticos dan imágenes amplificadas de los objetos colocados frente a ellos. Para entender cómo se forman estas imágenes, es necesario estudiar las trayectorias que siguen los rayos de luz que inciden en una lente biconvexa.
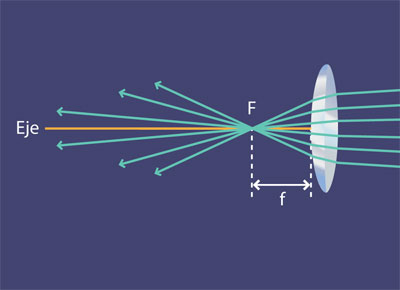
Si se considera una lente delgada (se denomina así a una lente que es muy delgada en comparación con su diámetro) biconvexa, como la mostrada en la figura 14; el eje de la lente es una recta que pasa por su centro y es perpendicular a sus superficies. Todos los rayos de luz que inciden en ella y que son paralelos a su eje se desvían de acuerdo con la Ley de Snell, convergiendo en el punto focal, que se representa con la letra "F". La distancia medida del punto focal al centro de la lente se conoce como distancia focal y se representa con la letra "f ".
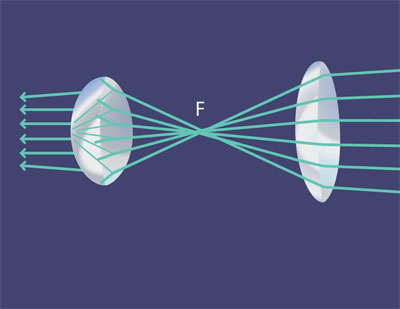
Si a la izquierda de esa primera lente se coloca una segunda lente biconvexa, de manera que su foco coincida con el foco de la primera, entonces, de la segunda lente y de acuerdo con la Ley de Snell, los rayos de luz saldrán paralelos al eje de la lente.
Para una lente biconvexa, un rayo de luz que incida en ella en dirección paralela a su eje se refractará pasando por su foco; un rayo de luz que incida en ella habiendo pasado por su foco se refractará saliendo de ella en dirección paralela a su eje, y un rayo de luz que incida en el centro de la lente pasará por ella sin desviarse.
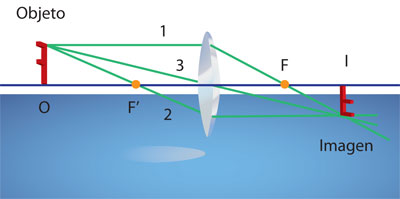
Con base en el comportamiento de estos tres tipos de rayos de luz que pasan por una lente biconvexa, es posible predecir algunas características importantes de las imágenes que pueden formarse con una lente de este tipo. En la figura 11 se muestran una letra F como objeto y una lente biconvexa que forma una imagen a la derecha. Seguiremos la trayectoria de sólo tres rayos de luz que salen de la parte superior de la F.
El rayo 1 se dibuja paralelo al eje; por lo tanto, al ser refractado por la lente, pasará por el punto focal F, situado detrás de ella.
El rayo 2 se dibuja pasando por el punto F, del mismo lado de la lente en que está el objeto; por lo tanto, emerge de ella paralelo al eje (si este tipo de lentes tienen dos puntos focales simétricos).
El rayo 3 incide en el centro de la lente y pasa sin desviarse.
Con dos de estos rayos basta para localizar el punto correspondiente a la imagen del punto del objeto (la esquina superior de la F, en este caso). Ahí donde se intersectan los rayos de luz, se localiza el punto imagen. Los puntos imagen correspondientes a los demás puntos del objeto pueden hallarse de la misma manera, hasta determinar la imagen completa del objeto. En este caso la imagen está invertida, respecto a la posición del objeto. Una imagen como ésta se llama imagen real, dado que los rayos de luz pasan realmente por la imagen y ésta puede ser captada en una pantalla, en una película fotográfica, aunque también se puede ver directamente.
El tamaño de la imagen obtenida dependerá de la distancia a la que se encuentra el objeto de la lente. Con estos diagramas de rayos se puede explicar por qué se ven algunas veces imágenes invertidas con la lupa.
El rayo 1 se dibuja, análogamente, sin mayor problema. Luego, el rayo 3 se dibuja fácilmente pasando por el centro de la lente sin desviarse. Como puede verse en la figura 12, estos dos rayos, al salir de la lente divergen, esto es, no se juntan en ningún punto, de modo que no pueden formar una imagen real. Pero si estos dos rayos divergentes se prolongan hacia atrás, se encuentra el punto en que estas líneas coinciden y en ese punto se forma la imagen de la esquina de la letra F. De hecho, se determina así la posición en que se forma una imagen y, como puede verse, se trata de una imagen virtual, pues los rayos de luz no pasan por la imagen; además, es derecha y de mayor tamaño que el objeto.
Para encontrar la distancia focal de alguna lente se necesita una fuente luminosa cuyos rayos sean paralelos. Puede ser el Sol, ya que la distancia a la que se encuentra de la Tierra es tan grande que se puede considerar que los rayos que pasarían por la lente son paralelos. También se puede quemar un papel usando una lupa y la luz del Sol; lo que se hace es justamente encontrar el foco. Por lo tanto, la distancia que hay entre la lupa y el papel cuando éste se empieza a quemar es justamente la distancia focal.
Una vez conocida la distancia focal, se pueden realizar diferentes experimentos colocando una lámpara a diferentes distancias de la lupa. Una hoja de papel al otro lado de la lente captará en ella la imagen de la lámpara. Se encontrará que si se pone la lámpara en el foco no se observa ninguna imagen, pero al colocarla entre el foco y dos veces la distancia focal, la imagen se proyectará amplificada e invertida, y la distancia a la que aparece la imagen nítida estará más allá del doble de la distancia focal.
¿Qué sucede si se pone la lámpara exactamente al doble de la distancia focal? La imagen aparecerá del mismo tamaño de la lámpara y la distancia a la que aparece la imagen invertida será el doble de la distancia focal. Si se pone la lámpara de dos veces más allá de la distancia focal se obtendrá una imagen reducida e invertida entre la distancia focal y dos veces la distancia focal.
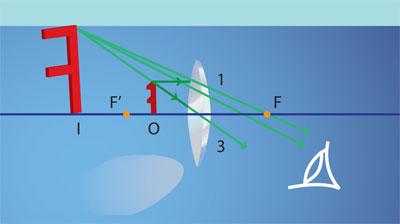
Ecuación de la lente. La ley de los puntos conjugados | Se puede obtener una ecuación que relaciona la distancia al objeto con la distancia a la imagen y con la longitud focal de una lente. Esta ecuación permite determinar la posición de la imagen de manera más rápida y precisa que mediante el trazado de rayos.
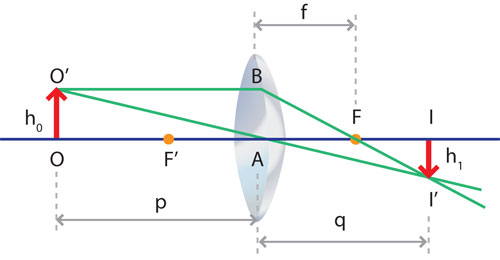
Considérese que "p" representa la distancia al objeto, esto es, la distancia del objeto al centro de la lente; "q" la distancia a la imagen o la distancia del centro de la lente a la imagen; y que "ho " y "hi" sean las alturas del objeto y de la imagen, respectivamente.
Considérense los dos rayos mostrados en la figura anterior, correspondientes a una lente delgada biconvexa.
Los triángulos FI'I y FBA son semejantes, pues el ángulo AFB es igual al ángulo IFI' , además de tener un ángulo recto cada uno de ellos. Así pues, por ser triángulos semejantes se cumple que:
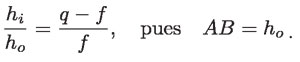
Por otro lado, los triángulos IAI' y OAO' , también son semejantes y por ello:
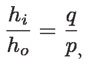
de manera que, igualando estas dos expresiones, se tiene que:
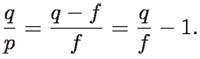
Dividiendo entre q:
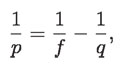
entonces:
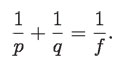
Esta ecuación es conocida como ley de los puntos conjugados, o ecuación de la lente, que relaciona la distancia a la imagen con la distancia al objeto y con la longitud focal. Entonces, si se conocen dos de estos datos, se puede calcular el tercero; ésta es la ecuación más útil de la óptica geométrica.
Microscopio compuesto | En realidad, una lupa es un microscopio simple, y se pueden ver con ella imágenes amplificadas de los objetos; puede tomarse como objeto una imagen real formada por otra lente.
Cuando se proyecta la imagen de un objeto en una pantalla, se coloca a ésta en la posición donde inciden los puntos luminosos correspondientes a puntos del objeto; pero aun cuando no se colocara la pantalla, los rayos de luz continuarían su camino, exactamente igual que si estuvieran saliendo de un objeto real. Entonces se puede tomar una imagen real como objeto de otra lente y conseguir así una mayor amplificación.
Considérese el siguiente diagrama, en cuyo arreglo se podría proyectar una imagen derecha de un objeto y de su mismo tamaño.
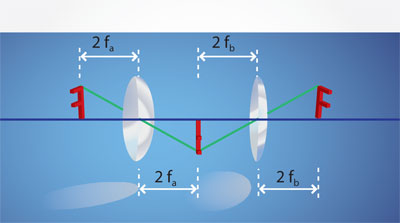
En este caso se tienen dos lentes biconvexas: la primera de longitud focal fa, y la segunda, de longitud focal fb. Se coloca el objeto a una distancia 2fa de la primera lente, de manera que se forma una imagen real, invertida y del mismo tamaño, a una distancia 2fa. Entonces, se coloca la segunda lente exactamente a una distancia 2fb de la primera imagen, de manera que se forma una segunda imagen (derecha respecto al objeto real) a una distancia 2fb de la segunda lente. Con esto se obtiene una imagen real derecha y de igual tamaño que el objeto real usando dos lentes biconvexas. Pero si se acerca la segunda lente a la primera imagen, de modo que la distancia sea menor que su distancia focal, y se observa a través de la segunda lente (llamada ocular) se verá una imagen virtual y de mayor tamaño que el objeto.
Se puede obtener una mayor amplificación si las distancias del objeto real a la primera lente son pequeñas, pero mayores que la distancia focal, de manera que con la primera lente se tendrá un primer aumento; esto es, que se genere una imagen real de mayor tamaño y luego se utilice el ocular para conseguir un aumento aún mayor. Éstas son las bases del microscopio compuesto.
Galileo (1564-1642) fue uno de los primeros científicos en utilizar un microscopio, incluso en Italia se considera que él fue el inventor de este instrumento, hacia el año 1610. Sin embargo, las primeras publicaciones importantes en el campo de la microscopía óptica aparecen a mediados del siglo XVII por el médico italiano Marcelo Malpighi (1628- 1694), quien probó la teoría del médico inglés William Harvey (1578-1657) sobre la circulación sanguínea, al observar al microscopio los capilares sanguíneos, y también por el científico inglés Robert Hooke (1635-1703), quien, al observar con un microscopio un delgado corte de corcho, descubrió y nombró células a los segmentos que formaban este material; de hecho esa fue la primera observación de células muertas.
A mediados de ese siglo, el biólogo y comerciante holandés Anton van Leewenhoek (1632-1723), utilizando microscopios de manufactura propia, describió por primera vez protozoarios, bacterias, espermatozoides y glóbulos rojos, de manera que este invento fue un pilar importante para el desarrollo de la biología y la medicina.
Al paso de los años los microscopios ópticos se perfeccionaron y surgió una gran variedad de éstos con mayor resolución, hasta llegar a los modernos microscopios electrónicos.
Otro instrumento óptico cuyo funcionamiento se basa también en el empleo de dos lentes delgadas es el telescopio; su uso ha contribuido al crecimiento y desarrollo de la sociedad. Aunque su invención alrededor de 1608 se atribuye al comerciante holandés Hans Lippershey, quien era dueño de una fábrica de anteojos en Middleburg, Holanda, se reconoce que Galileo fue uno de los primeros en estudiar el cielo con este tipo de instrumentos. Esto ocurrió en 1609, en Italia, con un telescopio fabricado por él mismo, para el cual utilizó una lente cóncava como ocular. Galileo observó la superficie de la Luna, encontrando que tenía cráteres y montañas, esto es, no era aquella esfera perfecta que muchos habían imaginado; observó también algunos satélites girando en torno a Júpiter y que Venus tenía fases como las de la Luna. Todas estas observaciones de Galileo le dieron elementos para apoyar la tesis del sistema heliocéntrico de Nicolás Copérnico, lo que causó que fuera enjuiciado por la Santa Inquisición. Pero, gracias a sus contribuciones, los sectores ilustrados de la sociedad, y luego la población en general, comenzaron a comprender y aceptar la posición de nuestro planeta en el Sistema Solar y en el Universo.
Cabe destacar que de los tiempos de Galileo a la fecha actual el telescopio se ha perfeccionado para captar imágenes de cuerpos ubicados a muchos años luz de nosotros. Hoy se dispone de un potente telescopio puesto en órbita terrestre: el telescopio espacial Hubble.
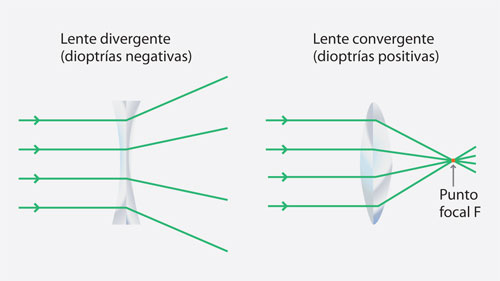
Los anteojos | Una lente cóncava, es decir, aquella que es más delgada en el centro que en los bordes, es una lente divergente puesto que hace que los rayos de luz, que inciden paralelos a su eje, diverjan (figura 15).
En este tipo de lentes el punto focal F es el punto del cual parecen emerger los rayos refractados que se originan en los rayos incidentes paralelos y, desde luego, la distancia entre el punto F y la lente, es la distancia focal f.
Los anteojos son instrumentos ópticos de uso común que basan su funcionamiento en el empleo de lentes cóncavas y convexas. Desde tiempos tan remotos como los de la Roma imperial, Nerón, debido a su miopía, utilizaba una esmeralda moldeada en forma cóncava, de media luna, para mirar las peleas de gladiadores.
Alrededor del año 1000 de nuestra era, el físico y matemático árabe Alhazen escribió un amplio tratado sobre óptica en el cual describió cómo se forma la imagen en la retina humana debido al cristalino del ojo, que es una lente convexa natural. Después, hacia 1266, el fraile franciscano inglés Roger Bacon talló los primeros lentes con forma de lenteja que ahora se conocen (de ahí su nombre de lentes) y describió las propiedades de una lente para amplificar la letra escrita. Así, a finales del siglo XIII en el norte de Italia, zona en que estaba muy desarrollada la tecnología del pulido de cristales, aparecen las primeras lentes convergentes.
Las primeras lentes se fabricaron para corregir la presbicia; eran convexas y se idearon inicialmente para un solo ojo; luego se unieron dos de esos lentes en una sola armadura y se les agregó un mango, para mayor comodidad. La armadura se colocaba sobre la nariz.
Las lentes cóncavas para miopes aparecen, aproximadamente, cien años más tarde. Se dice que ya las usaba el poeta y humanista italiano Petrarca (1304-1374). Con la invención de la imprenta en el siglo XV se incrementó la demanda de anteojos. Los primeros anteojos bifocales se inventaron en la segunda mitad del siglo XVIII Se dice que Benjamín Franklin fue de los primeros en usarlos. Así pues, aquellos primeros estudios sobre lo que hoy denominamos óptica geométrica, realizados por el físico árabe Alhazen, dieron las bases para esos dispositivos tan útiles a la sociedad en su necesidad de ver mejor.
Los optometristas y oftalmólogos utilizan el recíproco de la distancia focal (1/f) para referirse a la graduación de las lentes —ya sean convergentes o divergentes— para anteojos. La unidad empleada es la dioptría (D); 1D = 1/m = 1 m–1. Así, por ejemplo, una lente que tenga 50 cm de distancia focal tiene dos dioptrías (1/0.5 m = 2 m–1 = 2).
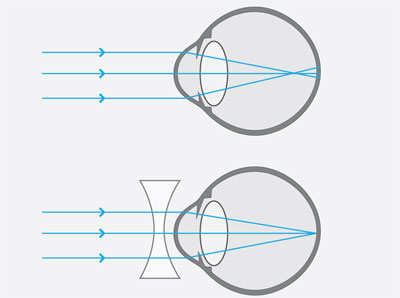
La miopía es la incapacidad de ver con claridad objetos lejanos; ocurre en un ojo demasiado alargado y, por lo tanto, la imagen de los objetos se forma delante de la retina.
Una lente divergente, que hace que los rayos de luz que llegan a ella paralelos se separen, permite que los rayos se enfoquen y formen la imagen de los objetos lejanos en la retina, corrigiendo así el defecto (figura 16).
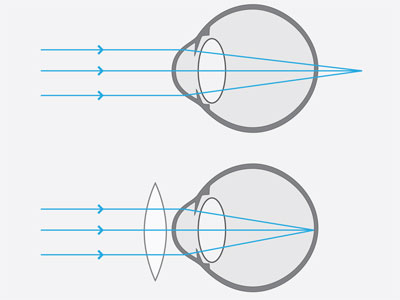
La hipermetropía consiste en la incapacidad de ver con claridad los objetos cercanos, lo que hace difícil la lectura. Este defecto ocurre en un ojo demasiado corto y los rayos de luz convergen atrás de la retina. Esta falla en la visión se puede corregir con una lente convergente (figura 17).
Con base en los primeros estudios de Alhazen se han construido también otros dispositivos que hoy son de uso cotidiano, como los binoculares, las cámaras fotográficas y los diferentes tipos de proyectores de imágenes. Por otro lado, con las aportaciones de Alhanzen, probablemente enriquecidas con los estudios del físico neerlandés Willebrord Snell (1591-1626) sobre la refracción de la luz de Isaac Newton, con sus propios descubrimientos sobre la dispersión de la luz blanca en los colores que la integran, dio explicación al maravilloso fenómeno natural del arcoiris.