Como se vio anteriormente, al hacer pasar una corriente variable (alterna) por una bobina, se genera un campo magnético; ahora, si se acerca otra bobina, en ésta se inducirá entonces una corriente.
Visto de otra forma, si se hace pasar una corriente variable por un circuito cerrado inducirá un voltaje en otro circuito cerrado. Este fenómeno, que consiste en la producción de un voltaje en otro circuito precisamente por medio de una corriente variable en algún otro lugar, fue descubierto por Michael Faraday (1791-1867) y por Joseph Henry de forma independiente en 1830. Una de las aplicaciones más comunes de la ley de Faraday son precisamente los transformadores, que constan de dos bobinas, una a la que se le llama primaria y otra secundaria. Por detalles técnicos se construyen de tal forma que la secundaria está enrollada sobre la primaria, de manera que por ambas pase la misma cantidad de líneas de campo magnético. El cociente de los voltajes en una y otra bobina está relacionado de la siguiente manera:
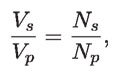
y por conservación de la energía, la potencia en la bobina primaria y en la secundaria son iguales:
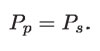
Pero P = VI, entonces,
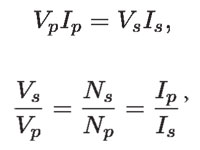
donde V s y Vp son los voltajes secundario y primario, respectivamente, Ns y Np son el número de vueltas de las bobinas secundaria y primaria, Is e Ip son lo propio para las corrientes como se muestra en el siguiente esquema.
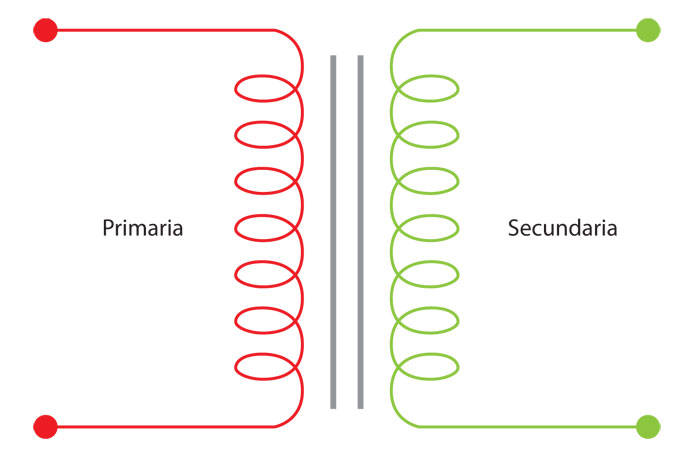
Ya sabemos que para que una bobina genere una corriente, ésta debe estar en presencia de un campo magnético que cambie con el tiempo, para lo cual, debe pasar por la primaria una corriente que cambie con el tiempo, esto es, debe ser alimentada con lo que llamamos corriente alterna, la cual, a diferencia de la corriente directa que se obtiene de una pila, pasa de ser positiva a negativa 60 veces por segundo.
De aquí que si se aplica un voltaje de corriente alterna a la bobina primaria, el voltaje inducido en la bobina secundaria puede ser mayor o menor, de acuerdo con el número de vueltas de cada bobina. Lo anterior se puede aplicar también a las corrientes de los transformadores de las calles que alimentan de electricidad a las casas, los cuales se rigen por esta sencilla ecuación.
Se sabe que se pierde una gran cantidad de energía al transportar la electricidad desde la planta que la genera hasta las casas, por lo que es necesario generar una mayor cantidad de energía en las plantas; sin embargo, si se aumentara la corriente, los cables se calentarían demasiado, por lo que, para transmitir energía eléctrica a grandes distancias, la corriente debe ser pequeña y el voltaje alto. Entonces, en la planta el voltaje es de 120 000 v, aproximadamente; al llegar a la ciudad se reduce el voltaje a 2 200 v con un primer transformador y, finalmente, con el transformador que está fuera de las casas, se reduce a 120 v.
Lo que se observa en la ecuación es que los voltajes y las corrientes están en relación inversa. Entonces, al llegar al transformador, se reduce el voltaje y se aumenta la corriente.
Por lo anterior, los científicos trabajan en encontrar materiales para hacer más eficiente el transporte de electricidad, como los superconductores o materiales que no presentan resistencia eléctrica, con lo cual se perdería muy poca energía en transportarla.
Hasta la fecha, los materiales que se han encontrado para este propósito sólo funcionan a temperaturas muy bajas (aproximadamente 200°C bajo cero, que es la temperatura del nitrógeno en su estado líquido), por lo que los cables se tendrían que enfriar a esta temperatura, lo cual sería muy costoso.
Otra propiedad de estos materiales es que expulsan el campo magnético de su interior, de modo que levitan en presencia de un imán. Un ejemplo de la aplicación de este fenómeno es el tren de levitación magnética Maglev, el cual tiene bobinas de material superconductor en la parte inferior y, conforme se desplaza, éstas inducen corriente en las bobinas fijas en el carril y actúan como imanes "espejo" que hacen levitar el tren a unos centímetros del riel, lo cual hace que no exista fricción entre el tren y el riel, haciéndolo muy rápido y eficiente (véase figura 19).
