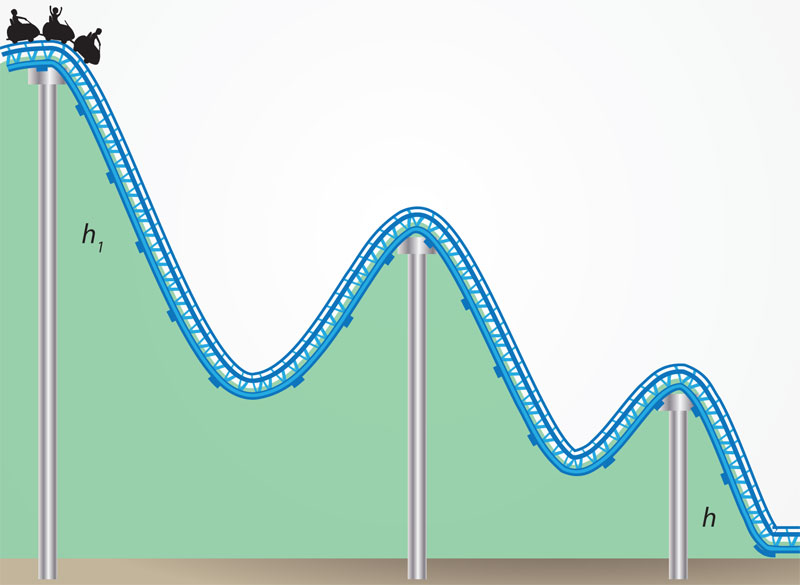
Una vez revisado lo relativo a la energía asociada al movimiento: la energía cinética, se analizará una energía asociada a la posición de un objeto respecto a otro. Si se estira una liga o se levanta del suelo un objeto a una cierta altura, se almacena una cierta cantidad de energía que llamamos energía potencial.
En el caso gravitacional, es decir, lo que sucede cuando dejamos caer el objeto que levantamos del suelo a una altura h1, la aceleración es (- g), y x es igual a h1; entonces:
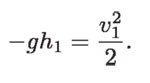
Multiplicando ambos lados por la masa m del cuerpo, se tiene:
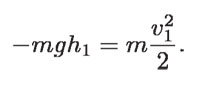
El lado izquierdo de la ecuación es la energía potencial del cuerpo en reposo antes de soltarlo, y el lado derecho es su energía cinética que tendrá al llegar al suelo.
Considerando ahora la suma de la energía potencial y la cinética en cualquier punto de su trayectoria de caída:
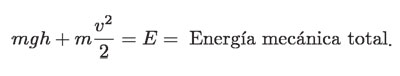
Para el punto más alto, cuando h=h 1, la velocidad del objeto es cero; por lo tanto, la energía mecánica total es:
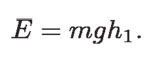
En el punto más bajo, h = 0:
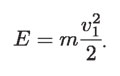
Por lo tanto, –mgh1= mv12/2 indica que la energía mecánica total se conserva en cualquier punto de la trayectoria. Este teorema de conservación es válido sólo en ausencia de fuerzas disipativas o de fricción.
La conservación de la energía total permite calcular la velocidad dada la altura en cualquier punto de la trayectoria, o viceversa. Una aplicación inmediata de esta ley de conservación podría ser el cálculo de la velocidad que llevará un carrito en una montaña rusa, dada la altura h1 de la cima inicial:
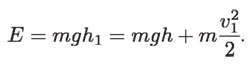
Para una altura h cualquiera tendremos que la velocidad es:
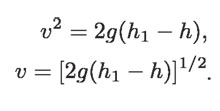
Esto es válido independientemente de las cimas que haya subido o bajado entre su posición inicial y la final a la altura h.
Nótese que si h = 0, recuperamos el valor de la velocidad de caída v1= (2gh1)1/2, y si h = h1, entonces v = 0.