Primera ley | La línea que va del Sol al planeta barre áreas iguales en tiempos iguales.
Segunda ley | Los planetas describen órbitas elípticas en las que el Sol se encuentra en uno de sus focos.
Tercera ley| Los cubos de los semiejes mayores de las órbitas elípticas planetarias son proporcionales a los cuadrados de los periodos de los respectivos planetas.
Con estas leyes y su verificación llevada a cabo con los satélites de Júpiter y Saturno, Newton formuló la ley de la gravitación universal, proponiendo que se cumple para cualquier cuerpo que esté en presencia de otro u otros.
Si se considera el caso especial de un planeta que recorre una trayectoria circular alrededor del Sol, entonces, la aceleración centrípeta será como se mencionó anteriormente:
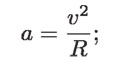
para un círculo, por lo que
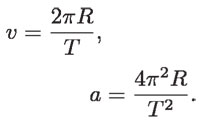
Ahora, de la tercera ley de Kepler:
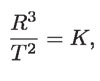
de la cual obtenemos que
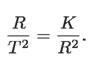
Así que
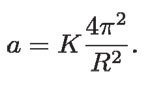
Entonces, enunció su ley diciendo que:
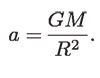
En esta ley, M representa la masa del cuerpo atractor y G es la constante de gravitación universal. Es decir, la aceleración gravitacional que un cuerpo le imparte a otro es inversamente proporcional al cuadrado de la distancia que los separa y directamente proporcional a una característica del cuerpo atrayente, a la que Newton le llamó "carga gravitatoria". Él observó que esta característica era mayor cuanto mayor era la "cantidad de materia" del cuerpo atrayente, y en consecuencia, la identificó con la masa gravitacional.
Esta ley fue comprobada en todos los casos conocidos y permitió a Simon Laplace (1749- 1827) construir su trascendental Mecanique Celeste. Pero no sólo esto, sino que sentó las bases para predecir la existencia de otros planetas, como Neptuno por Leverrier (1811-1877). En la actualidad la ley explica satisfactoriamente el comportamiento de las estrellas binarias y la existencia de planetas en estrellas.