Fue Newton al que se le ocurrió relacionar el movimiento de los cuerpos que caen a la superficie de la Tierra y el movimiento circular de la Luna en torno de la Tierra. Este razonamiento genial llevó a Newton a realizar cálculos basados en experimentos que culminaron con encontrar que ambos eran movimientos acelerados y que la causa de esta aceleración era la atracción gravitatoria dirigida hacia el centro de la Tierra.
¿Cómo se le ocurrió relacionar estos movimientos? ¿Cuál es la diferencia entre el movimiento del cuerpo que cae y el de la Luna? En efecto, ambos son movimientos acelerados y la causa de la aceleración es la misma: la atracción gravitatoria de la Tierra. Si los efectos no son los mismos, es debido a que las condiciones iniciales no son las mismas; la Luna tuvo alguna vez una velocidad inicial particular, que la hace describir una órbita circular, en cambio el cuerpo que cae, lo hace verticalmente hacia la Tierra. En ambos casos se trata de una caída provocada por una fuerza dirigida hacia el centro de la Tierra.
El sentido común indicaría que al lanzar un cuerpo hacia arriba, llegará a una cierta altura y después caerá; si lo lanzamos con más velocidad, llegará más alto y tardará más en caer. Si aumentamos y aumentamos la velocidad, llegará más lejos, pero siempre caerá, a menos que llegue a la velocidad para escapar de la Tierra, llamada velocidad de escape. ¿Qué ocurre si disparamos un proyectil en dirección paralela a la superficie de la Tierra, desde una altura y con una velocidad dadas? Si aumentamos la velocidad, el proyectil llegará cada vez más lejos. Si se considera el efecto de la curvatura de la Tierra, las órbitas que se obtienen son círculos, elipses o parábolas.
Por otro lado, ¿cómo podemos determinar la magnitud de la aceleración circular?
Desde luego esta aceleración será radial, esto es, hacia el centro del círculo. Christiaan Huygens (1629-1695) calculó esto. Supuso un cuerpo que se encuentra en A y que en su movimiento describe el arco de círculo AC en un tiempo t. Si no existiera una aceleración a, el cuerpo seguiría de A hasta B en movimiento rectilíneo uniforme, de modo que
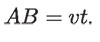
Pero, por causa de dicha aceleración, se produce la "caída" BC que, de acuerdo con la Ley de Galileo, vale:
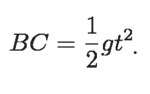
En el triángulo rectángulo OAB de la siguiente figura, se tiene que OA = OC = R, que es el radio del círculo.
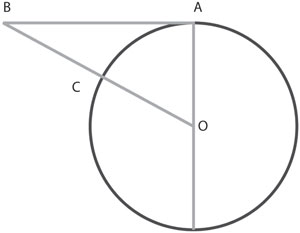
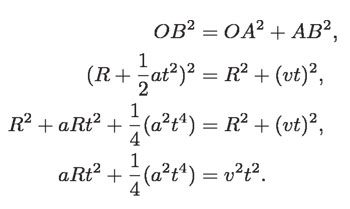
Dividiendo por t2
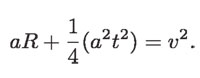
Para tiempos muy pequeños, lo que es necesario para explicar una curva continua, se puede despreciar el término que contiene a t2 y llegar al resultado:
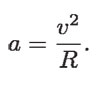
Ahora se puede calcular el valor de la aceleración que hace girar a la Luna alrededor de la Tierra, sustituyendo su velocidad y la distancia del centro de la Tierra al centro de la Luna; con estos valores se obtiene que:
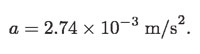
Después se le ocurrió a Newton que estos resultados se podrían generalizar al caso del Sistema Solar. Claro que este problema era mucho más complicado, ya que en este caso, ni las órbitas son circulares (sino que son elipses), ni la velocidad de los planetas es constante.
El movimiento de los planetas fue un problema que interesó a los astrónomos desde Ptolomeo hasta Copérnico, y fue Johanes Kepler quien, analizando las observaciones planetarias de Tycho Brahe, pudo resumir dicho movimiento en tres leyes que llevan su nombre.