Cuando sobre un objeto actúa una fuerza neta diferente de cero, entonces la velocidad del objeto cambia; el cambio puede ser aumento o disminución en su magnitud, en su dirección o en ambas. Podemos decir también que todo cambio en la velocidad de un objeto es debido a la acción de una fuerza no balanceada que actuó sobre él.
En la segunda mitad del siglo XVII, Isaac Newton analizó esta relación entre fuerza neta y cambio de velocidad, pasando a formar parte de las leyes del movimiento, las cuales son la base de su magna obra Philosophiae Naturalis Principia Mathematica, publicada en 1687. Newton, para algunos el más grande científico de la historia, declaró: "Si he visto lo que muchos otros no han podido ver, es porque he estado montado en hombros de gigantes." Esta declaración es un reconocimiento a que sus trabajos e investigaciones tuvieron como base los aportes de algunos sabios que lo precedieron, como Galileo Galilei, Johannes Kepler y Tycho Brahe.
Newton supo de los experimentos de Galileo y de las reflexiones de Descartes sobre la inercia, esa tendencia de los objetos a conservar su estado de movimiento rectilíneo o de reposo. Observó que la inercia de los objetos dependía directamente de su masa; los objetos muy masivos presentan una inercia muy grande, es decir, una gran tendencia a conservar su estado de movimiento rectilíneo o de reposo. Esto lo llevó a razonar que la aceleración que experimenta un objeto depende tanto de la fuerza neta aplicada como de su masa.
Experimentando encontró que la velocidad de un objeto varía de manera inversa con la masa. Es decir:
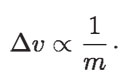
Esto es, cuando la masa aumenta, el cambio en velocidad disminuye. Además, el cambio en la velocidad de un objeto varía directamente con la fuerza neta aplicada.
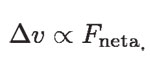
Es decir, el cambio en la velocidad aumenta cuando la fuerza neta aumenta. De estas dos relaciones de proporcionalidad, concluyó que:
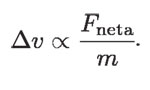
De esta expresión se desprende que si se fija el valor de la fuerza neta, entonces el cambio de velocidad varía de manera inversa con la masa. Ahora, si se fija la masa y se varía la fuerza neta, entonces el cambio en la velocidad varía directamente con ésta.
Pero mientras esté actuando la fuerza neta sobre el objeto, la velocidad de éste estará cambiando; por lo tanto, el cambio total que experimente la velocidad tendrá que ser grande, si el intervalo de tiempo durante el cual actúa la fuerza es grande. Esto es, Δv varía de manera directa con el intervalo de tiempo Δt, es decir:
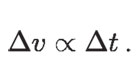
Se pueden reunir las dos relaciones de proporcionalidad anteriores, en una sola:
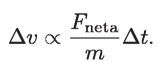
Esta relación nos dice que el cambio de velocidad de un objeto varía de manera directa con la fuerza neta aplicada, en el intervalo de tiempo durante el cual dicha fuerza se aplica y de manera inversa con la masa del objeto.
Ahora, en esta última relación multiplicamos a ambos lados por m:
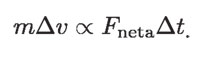
Entonces, si llamamos k a la constante de proporcionalidad:
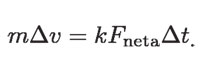
Si las cantidades involucradas en esta relación de proporcionalidad se expresan en las unidades del Sistema Internacional, resulta que k = 1 y por lo tanto:
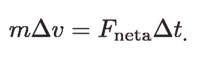
Esta ecuación es muy parecida a la que usó Newton para relacionar a la fuerza neta que actúa sobre un objeto con el cambio en su estado de movimiento, y nos permite cuantificar el cambio en velocidad que experimenta un objeto de masa m al aplicarle una fuerza neta conocida durante el intervalo de tiempo Δt.
Recordando que todo cambio en la velocidad es un indicador de la existencia de aceleración y utilizando este concepto, se obtiene una expresión que relaciona la fuerza neta con la aceleración. Dividiendo la ecuación anterior entre Δt, queda:
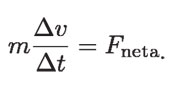
En esta ecuación aparece el cociente del cambio de velocidad Δv, entre el intervalo de tiempo que dura ese cambio, Δt. Como es sabido, Δv / Δt es la aceleración del objeto en ese intervalo de tiempo, así:
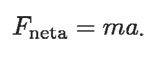
De esta ley se puede concluir que:
Dado el movimiento, se puede encontrar la fuerza que lo produce o dada la fuerza, se puede encontrar el movimiento.
La ecuación anterior es la representación más conocida de la llamada segunda ley de Newton. En el SI, m se mide en kilogramos (kg), a se mide en metros sobre segundo al cuadrado (m/s2) y Fneta, se mide en newtons (N). Así, se puede decir que un newton es la fuerza que, aplicada a un objeto cuya masa es de 1 kg, le produce una aceleración de 1 m/s2.