Si analizamos el movimiento de una hoja de papel delgado, como un filtro de café que cae libremente, es decir, sin que nadie lo empuje, observamos que éste cae a velocidad constante, atraído por la Tierra. ¿Qué ocurre con la caída si al filtro se le cambia de forma, por ejemplo, formando una bola?, ¿y si se le da forma de lanza, en qué caso cae primero?, ¿la rapidez de caída de estos objetos depende de la forma que se les dio?, ¿el aire interviene en la explicación de esta diferencia? Si dejamos caer dos objetos al mismo tiempo, nos daremos cuenta de que el más compacto cae más rápido.
Ahora, imaginemos un tubo de vidrio o plástico al que se le ha extraído el aire y dentro de él se dejan caer simultáneamente: una pluma de ave y una canica. Se observará que caen al mismo tiempo. De estas experiencias, se pueden sacar dos conclusiones:
a] Lo objetos en el aire tardan tiempos diferentes en caer, dependiendo de su forma.
b] Cuando no hay aire todos los objetos caen en el mismo tiempo, sin importar su forma y composición.
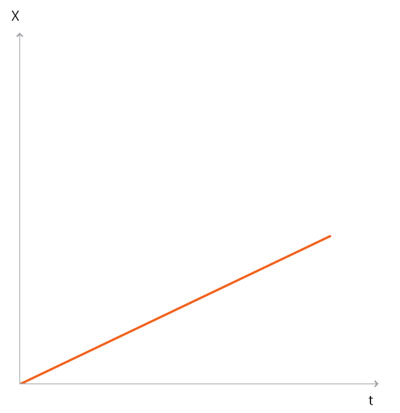
El caso del movimiento vertical del filtro de café se muestra en la figura 9 (x, t).
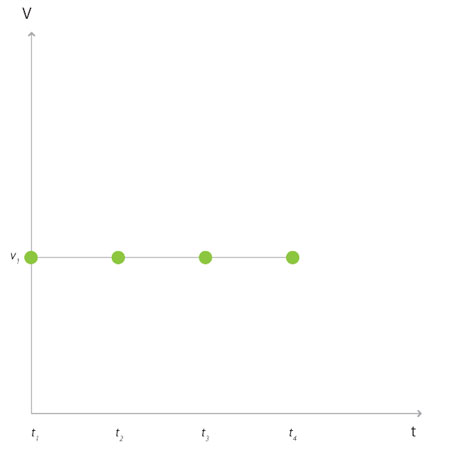
Para una mejor descripción del movimiento, se representa la rapidez y el tiempo, en donde el eje vertical es la rapidez (v) y el horizontal es el tiempo (t), como se ve en la figura 10. Aquí, al movimiento del filtro de café le corresponde una línea horizontal, lo que quiere decir que la rapidez no cambia con el paso del tiempo, es constante.
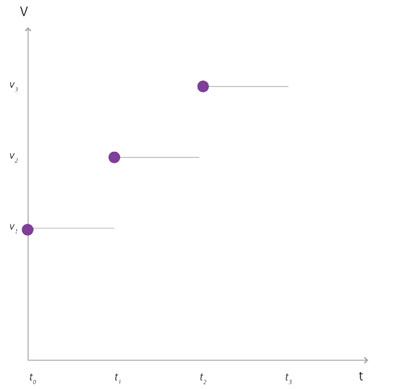
Pensemos ahora en un movimiento de caída más complejo, en el cual del tiempo t0 al tiempo t1 el objeto se mueve con una rapidez v1. Del tiempo t1 al tiempo t2el objeto se mueve con una rapidez v2 mayor que v1; del tiempo t2 al tiempo t3 el objeto se mueve con una rapidez v3 mayor que v2 y así sucesivamente, como se muestra en el diagrama (figura 11).
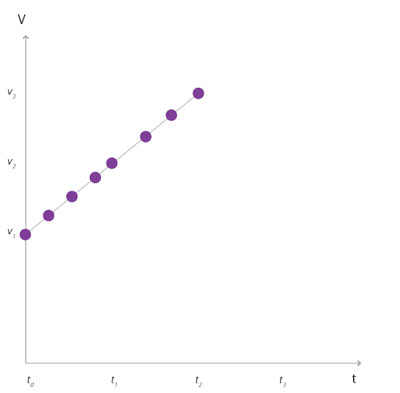
En este caso, la rapidez es constante en cada uno de los intervalos de tiempo, pero a su vez crece formando una escalera. Si estos intervalos son cada vez más pequeños, entonces los peldaños reducen su ancho hasta convertirse eventualmente en puntos. Si los unimos obtenemos una recta con cierta inclinación. Véase figura 12.
¿Cómo sería la correspondiente gráfica (x, t) para este movimiento? Recordemos que cuando estudiamos el movimiento con velocidad constante, vimos que su gráfica (x, t) era una recta cuya inclinación es proporcional a la rapidez. Como la rapidez se incrementa en cada intervalo de tiempo, la inclinación de la recta en cada intervalo será cada vez mayor.
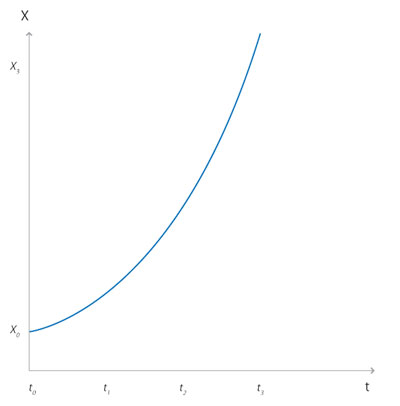
Si hacemos estos intervalos muy pequeños, las rectas inclinadas se convierten en puntos que, al unirlos, nos dan una curva continua creciente (figura 13).
Decimos que un objeto se acelera cuando aumenta su rapidez y que se desacelera en caso contrario.
En la historia de la ciencia se registran diferentes respuestas al estudio del movimiento de los objetos sobre la superficie de la Tierra, empezando por el problema de la caída de los cuerpos en presencia del aire. La caída en el vacío es imaginada hasta el siglo XVII, en Europa, sobre todo a partir del invento de la bomba de vacío en 1650 por Otto von Guericke (1602-1686).
Pero no sabemos lo que al respecto pensaban los científicos en distintas culturas de la Antigüedad, como los mayas o los babilonios, pues no hay registro de su pensamiento. Ni siquiera sabemos con certeza si era un problema que les importaba, aunque la evidencia indirecta, como el diseño del átlatl, presente en muchas culturas de la Antigüedad, demuestra que el movimiento de lanzas sí era un problema importante al que, además, le dieron una brillante solución.
Otro ejemplo es el movimiento de piedras lanzadas a mano o por hondas; de hecho, el invento de la honda es un ejemplo de la existencia de la solución a una necesidad.