Una onda es un movimiento oscilatorio que se propaga en un medio. En las ondas, como las que se producen en un estanque donde se ha lanzado una piedra, el movimiento oscilatorio del agua es perpendicular o transversal a la dirección en que la onda se desplaza; a éstas se les denomina ondas transversales. Esto mismo sucede en una onda transversal producida en un "resorte de gusano".
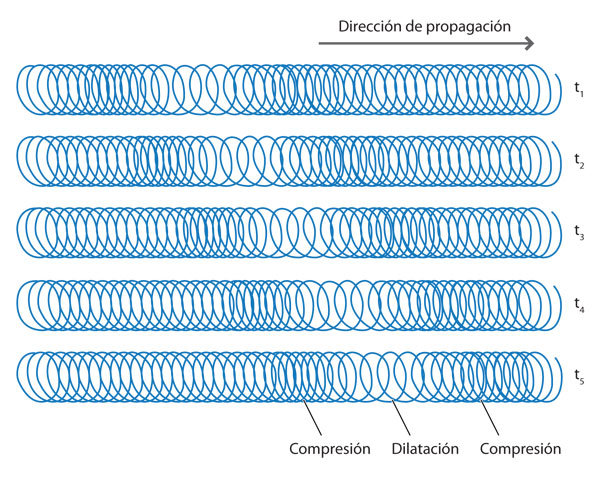
En las llamadas ondas longitudinales, que también pueden transmitirse en un "resorte de gusano", el movimiento de un paquete de espiras es hacia adelante y hacia atrás, en la misma dirección en que longitudinalmente ocurre la propagación de la onda.
En los casos de ondas transversales y longitudinales, las partículas del medio (del agua o del resorte), que oscilando producen la onda, no se trasladan con ella. Lo que la onda transporta es una señal, que es precisamente el movimiento oscilatorio local del medio (figura 5).
La ola en un estadio de futbol nos permite ver lo dicho con más sencillez y claridad. Como dato curioso, la ola fue inventada por aficionados mexicanos, durante el campeonato mundial de futbol en 1986 en nuestro país. A una señal, un grupo de aficionados cercanos entre ellos, situados sobre una hilera de asientos, se levanta del asiento levantando al mismo tiempo los brazos y, en seguida, se sientan bajándolos.
Con un movimiento oscilatorio arriba-abajo, los vecinos de uno de los lados, por ejemplo del derecho, inician con un ligero retraso su propio movimiento arriba-abajo consiguiendo, con esto, estar completamente de pie una fracción de segundo después de que el vecino lo hizo. Y así para cada hilera, lo que se ve en el estadio es la propagación de la señal inicial; se ha producido la ola.
En algunos aspectos, un tsunami y un terremoto son olas como las del estadio. Pero, mientras que la ola en el estadio de futbol no ocasiona daños, un tsunami o un terremoto son capaces de provocar una catástrofe.
En el caso de la ola, la señal o perturbación que se propaga es el movimiento oscilatorio arriba-abajo de las personas, pero ellas no avanzan con la onda, pues se quedan en su lugar. Podemos decir que, en este caso, la ola es la propagación de una perturbación sin transporte de materia.
Ahora bien, la importancia del movimiento ondulatorio radica precisamente en que éste es capaz de transmitir una señal, que a su vez es capaz de producir un efecto físico en algún receptor. Es el caso del oído, que al captar las compresiones del aire, producidas por las ondas, hace que las percibamos como sonido. El sonido nos trae señales que contienen información, como las palabras o la música. En los tsunamis y terremotos, desgraciadamente, el objeto receptor de la señal es el ambiente y las poblaciones.
Otro tipo de ondas, como las electromagnéticas, transportan señales que son la base de las telecomunicaciones y son indispensables para nuestra civilización. Actualmente no se puede pensar en un mundo sin televisión, teléfonos celulares, radio o Internet. Sin las ondas electromagnéticas tampoco habríamos podido generar nuestra concepción del Universo, pues la información de su estructura nos llega mediante este tipo de ondas. Lo mismo podemos decir en relación con el conocimiento actual del mundo atómico y subatómico.
Una descripción más detallada de las características del movimiento ondulatorio tanto para ondas longitudinales como transversales, tomando como ejemplo al "resorte de gusano", es la siguiente:

Ondas longitudinales son aquéllas en que las partículas del medio oscilan en la dirección en que avanza la perturbación.
Ondas transversales son aquéllas en que las partículas del medio oscilan en dirección perpendicular a aquella en que se propaga la perturbación (figura 6).
Desde luego que las partículas del medio sólo oscilan en torno a un punto, pero no viajan con las ondas, es decir, las ondas no transportan materia; entonces, ¿qué es lo que transportan las ondas? Transportan una señal en forma de perturbación del medio de propagación.
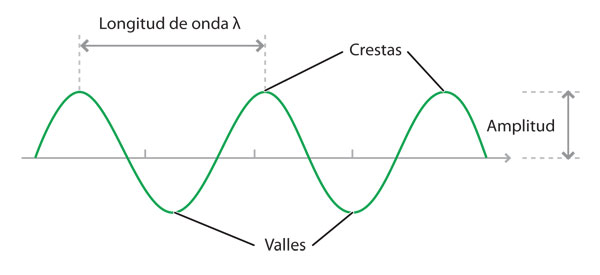
En la propagación de ondas transversales, en el anterior diagrama se pueden identificar algunos parámetros básicos:
• Los puntos máximos y mínimos se denominan crestas y valles, respectivamente.
• El tamaño de una cresta o valle representa la amplitud de la onda A.
• La distancia entre dos crestas o dos valles consecutivos se denomina longitud de onda, se representa con la letra λ del alfabeto griego (se lee lambda) y se mide en metros, como cualquier otra longitud.
• El tiempo en que se repite una onda completa se conoce como periodo, se representa con la letra T y se mide en segundos.
• El número de ondas completas que pasan por un punto en una unidad de tiempo es la frecuencia, que se representa con la letra f. Si una onda completa pasa en un segundo tiene una frecuencia de un Hertz (y se denota 1 Hz). De modo que si en un segundo pasan 100 ondas, tendremos una frecuencia de 100 Hz. Una onda de radio tiene una frecuencia que puede llegar a más de 100 mega Hz, es decir, se repite más de cien millones de veces en un segundo, y hay frecuencias mucho más grandes.
El periodo y la frecuencia están íntimamente relacionados. Por ejemplo:
• Si el periodo es de un segundo, la frecuencia será de 1 Hz.
• Si la frecuencia es de 2 Hz, ocurren dos ondas en un segundo; cada onda se completa en 1/2 segundo y éste es su periodo.
• Si el periodo es de 1/10 s, la frecuencia será de 10 Hz y así sucesivamente.
De tal forma que la frecuencia y el periodo son recíprocos, es decir, el producto de la frecuencia por el periodo es siempre 1.
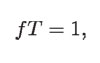
por lo tanto
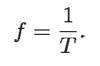
Lo cual quiere decir que cuando la frecuencia crece, el periodo decrece y viceversa. Ahora, la propagación de las ondas tiene también una velocidad, como en el caso del movimiento rectilíneo. Para calcular la velocidad de propagación de las ondas en el resorte de gusano, consideramos n ondas de la misma longitud λ en un intervalo de tiempo Δt = t2 – t2 = nT. Las "n" ondas ocupan una longitud total Δx = x2 – x2 = nλ.
Entonces, la velocidad de las ondas será:
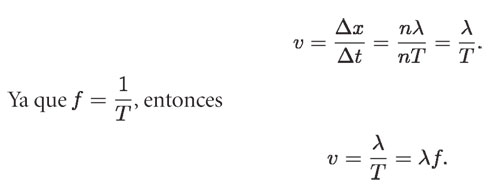
Se ha mencionado que las ondas se pueden propagar en materiales líquidos, gaseosos y sólidos. Si imaginamos a un sólido como formado de átomos y moléculas fuertemente unidas por resortes duros, y que los átomos y moléculas de un líquido están débilmente unidos por resortes "blandos", entonces se puede predecir correctamente que las ondas viajan más rápido en los sólidos que en los líquidos.
¿Qué ocurre con el sonido? Imaginemos a un peatón que pasa frente al patio de una escuela y oye los gritos y risas de los estudiantes, a pesar de la gruesa barda que la rodea. A este efecto del sonido doblando esquinas y saltando bardas se le llama difracción y es tan común que muy poca gente le presta atención. La difracción por obstáculos se puede presentar cuando las dimensiones de éstos son del tamaño de la longitud de onda del sonido.
Pero si la longitud de onda es muy pequeña comparada con los obstáculos, la onda no los rodea, no se difracta; se produce una "sombra de sonido" muy bien definida, de manera que para escuchar el sonido habría que situarse sobre una línea recta sin obstáculos entre el que escucha y el lugar de donde proviene el sonido.
Cuando las ondas sonoras inciden sobre una superficie, una parte de su intensidad es absorbida y el resto se refleja. Las ondas sonoras se absorben mejor en las superficies blandas; por ejemplo, las cubiertas con materiales como fieltro, corcho, algodón o alfombras, que se utilizan para recubrir las paredes de teatros y cines.
Las perturbaciones en el aire, producidas por las vibraciones de un objeto, por ejemplo, las producidas por la superficie de un tambor, se propagan longitudinalmente como en uno de los casos del "resorte de gusano". En la figura 8 se puede observar que las espiras comprimidas del resorte corresponden a una capa de alta densidad de aire y las espiras extendidas del resorte a una capa de baja densidad, representadas por zonas oscuras y claras, respectivamente.

La "dureza" o la "blandura" de un resorte se caracteriza diciendo que tiene baja o alta elasticidad, dependiendo de si, con el mismo esfuerzo, se estira poco o mucho. Robert Hooke (1635-1703), físico inglés contemporáneo de Newton, hablaba, en 1680, del "resorte del aire" para indicar que su compresión se parecía a la compresión de un resorte. Como la elasticidad del aire es menor que la de un sólido, por ejemplo un metal, una onda se propagará en el primero con menor rapidez.