Como ya se ha mencionado, para describir el movimiento es necesario tener una referencia. Es muy difícil saber lo que ve, oye o siente otra persona y notar que el mundo que percibimos puede ser diferente, es decir, que el mundo que vemos depende desde dónde lo vemos, esto es, depende del punto de referencia. ¿Nos alejamos o nos acercamos? ¿Estamos arriba o abajo?
Para responder a estas preguntas debemos indicar respecto a qué o desde dónde observamos. Si no se especifica el punto de referencia en cada caso la respuesta puede ser diferente, y aun así correcta. Incluso podemos llegar a descalificar a la otra observación, porque simplemente tiene otra referencia.
Sin embargo, hablando de movimiento, el que un cuerpo se mueva quiere decir que pasa de un lugar a otro; esto es, que primero ocupaba una posición y luego otra; sin perder de vista que las posiciones y los cambios de posición son respecto a una referencia.
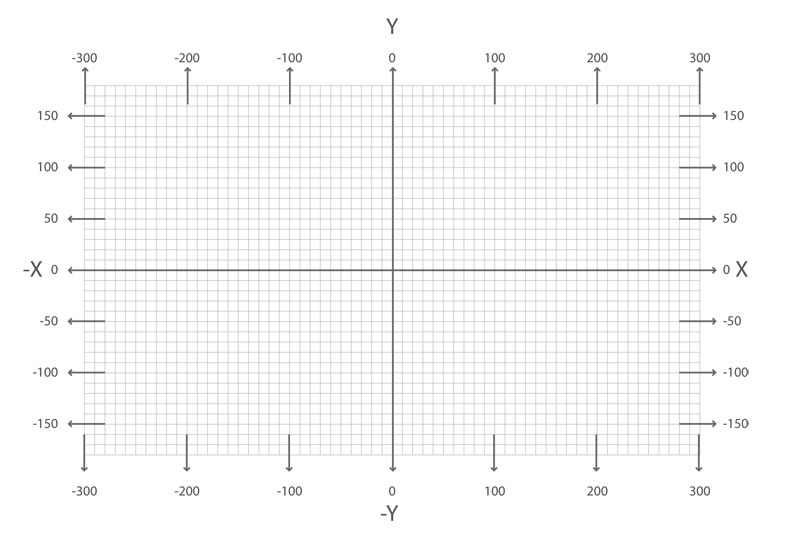
En física, como se verá más adelante, al estudiar el movimiento usamos el concepto de marco de referencia, que es un esquema geométrico compuesto por dos rectas perpendiculares, sobre las cuales se pueden ubicar distancias; el origen de esas distancias es el punto donde se cruzan las dos rectas (figura 1). Este esquema fue ideado por el científico francés René Descartes (1596-1650).
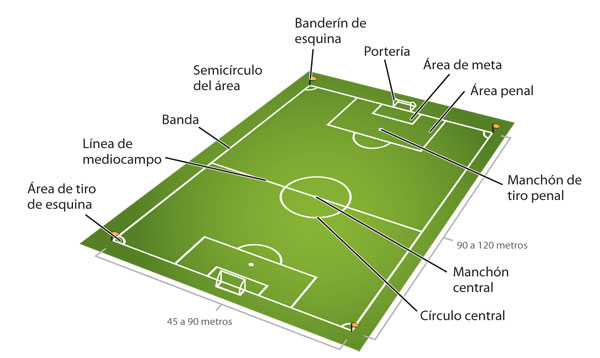
Para ilustrar lo anterior se puede pensar en un partido de futbol en donde el movimiento de los jugadores y el balón durante el juego se indica tomando como referencia las características de la cancha y sus divisiones: área chica, área grande, medio campo, círculo central; línea de meta, banda lateral, esquinas y manchón de penalti (figura 2).
Con estos conceptos se pueden relatar las jugadas de forma más precisa. "El balón de tiro de esquina fue tomado de palomita por el centro delantero en el área chica, a la altura del manchón de penalti y salió un cabezazo al ángulo superior derecho del poste contrario que dejó parado al portero. ¡Fue un golazo!" Como lo narraría un buen cronista.
Si se quiere describir la jugada anterior sin emplear las palabras "esquina", "área chica", "manchón de penalti", "ángulo superior derecho", "poste contrario", no se puede. Cada una de ellas son referencias que nos dan una idea del movimiento del balón; sin ellas no se podría saber su localización, ni por dónde se movió. No se puede dar una descripción de lo que llamamos trayectoria. Además, en la descripción de la jugada, también se usaron los términos de "cabezazo" y "dejar parado al portero". Ambos conceptos tienen que ver con la rapidez de la acción y, con ellos, se complementa la descripción del movimiento del balón, el cual se compone de dos conceptos: trayectoria y velocidad.
Además, para dar una descripción más exacta de la jugada, se requiere saber ¿dónde estaban precisamente los demás jugadores y cómo se movían?, ¿en qué dirección y sentido?, ¿lenta o rápidamente?, así como una descripción precisa del movimiento del balón. Es decir, se requiere de una descripción geométrica del movimiento.
Entonces, para la descripción geométrica del movimiento se requiere de un marco de referencia, dentro del cual pueda definirse con precisión una trayectoria, que es la línea que marca la posición de un objeto en el espacio durante su recorrido.
En el ejemplo del campo de futbol hay lugares que pueden especificarse fácilmente, como el centro del círculo central; mientras que los manchones de penalti necesitan adicionalmente que se especifique si es el de uno u otro lado de la cancha; las esquinas de las áreas chica y grande también requieren de referencias adicionales; las cuatro esquinas del campo demandan que se diga el lado de la cancha a que pertenecen y, además, si es la superior o la inferior. Así que si el balón o el jugador se hallan sobre cualquiera de los lugares anteriores, su posición queda bien determinada.
Pero, ¿qué sucede en cualquier otro lugar?
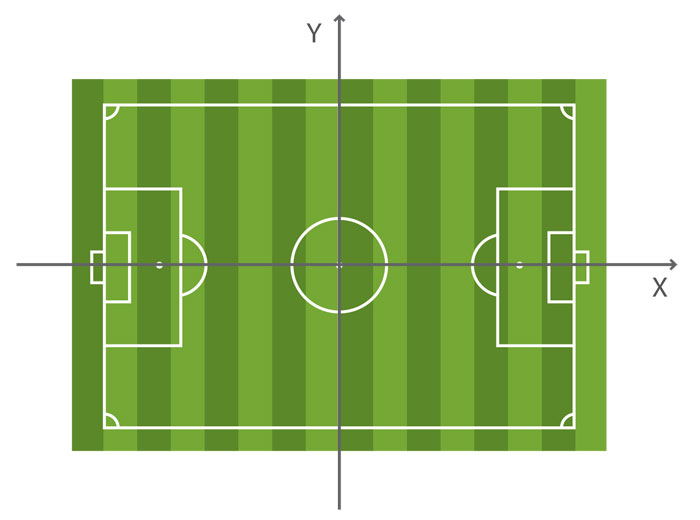
Si se recurre a un marco de referencia cartesiano, un punto cualquiera sobre el terreno queda determinado por un par de números; a éstos les llamamos coordenadas. A la línea horizontal le llamamos eje x y eje y a la línea en el plano perpendicular a ella. Con esto, la localización de un punto cualquiera se denota por un par de números dentro de un paréntesis (x, y). De este modo, ya se puede determinar la posición del balón y de los jugadores sobre la superficie, pues para ello simplemente se dan las coordenadas (x, y) de cada uno de los objetos (figura 3, p. 322). [Véase animación en CD: "Jugada de futbol 2D".]
Sin embargo, falta la altura que lleva el balón. Esto se puede representar asignando un tercer número que indique la altura sobre el plano, representado por la letra z.
Es claro que el movimiento del balón ocurre en un espacio de tres dimensiones y, por lo mismo que antes, se requieren tres números para fijar su posición. El espacio de tres dimensiones es en el que nos movemos. De esta forma el balón y los jugadores pueden localizarse simplemente dando las coordenadas de cada uno, según los tres números (x, y, z). [Véase animación en cd: "Jugada de futbol 3D".]
Un último aspecto es el que tiene que ver con la rapidez con que se mueve el balón. Para esto se debe introducir el tiempo en la descripción del movimiento y definir los conceptos de rapidez y sentido.
Para introducir el tiempo en la descripción geométrica del movimiento tendríamos que asignar a cada punto un tiempo, que representamos por la letra t; ahora los cuatro números (x, y, z, t) marcan la posición de un evento en un espacio de cuatro dimensiones. Este espacio es el espacio de eventos de cuatro dimensiones que describe completamente el movimiento del objeto.