Hay una diferencia notable con el caso que enfrenta Úrsula al adivinar el disco que Arcadio le compró. Allí sí se sabe algo, no se parte de que fue elegido de manera completamente aleatoria. Poniéndolo en otros términos, las listas de popularidad, los conocidos "top 10" o "top 40" de discos, se forman contando cuántos discos se venden de cada intérprete o artista; es decir, con base en estadísticas. Así que lo que la lista dice es algo como:
si x está arriba de y es porque es más frecuente que un cliente cualquiera compre el disco x y no el y; podría ser, por ejemplo, que de cada 100 discos comprados, 37 sean x y 23 sean y. Un árbol de decisión eficiente para determinar qué disco compró Arcadio debe tomar en consideración ese hecho. En cuanto Úrsula supo que Arcadio le había comprado un disco de regalo, intentó preguntar por cosas que fueran más probables de ocurrir. Cuesta menos trabajo deducir algo muy común que algo raro. Si Arcadio le hubiera comprado un disco de música medieval letona, Úrsula hubiera tenido que hacer más preguntas para adivinar.
En cualquier representación de datos que pretenda ser eficiente se debe utilizar un criterio análogo al de la "popularidad": decir que ocurrió algo que todo mundo sabe que ocurre muy frecuentemente no es noticia; en otras palabras, aporta poca información o se requieren pocas preguntas para deducir qué ha ocurrido. En cambio, cuando lo que ocurre es un evento raro, fuera de lo común, sí se necesita mucha información para deducirlo y, por tanto, para representarlo.
La estrategia de la representación eficiente entonces es considerar qué tan probables son los datos que se pretende representar. Si un dato aparece 70 veces en un conjunto de 100, lo ideal sería que la longitud de su representación fuera la mitad de la usada para otro que ocurre 35 veces. Datos más frecuentes corresponden a longitudes de representación menores, porque hay que decirlos más seguido y conviene decir menos las más de las veces. Datos menos frecuentes corresponden con longitudes mayores porque, como se dicen pocas veces, se necesita más información para que puedan ser determinados.
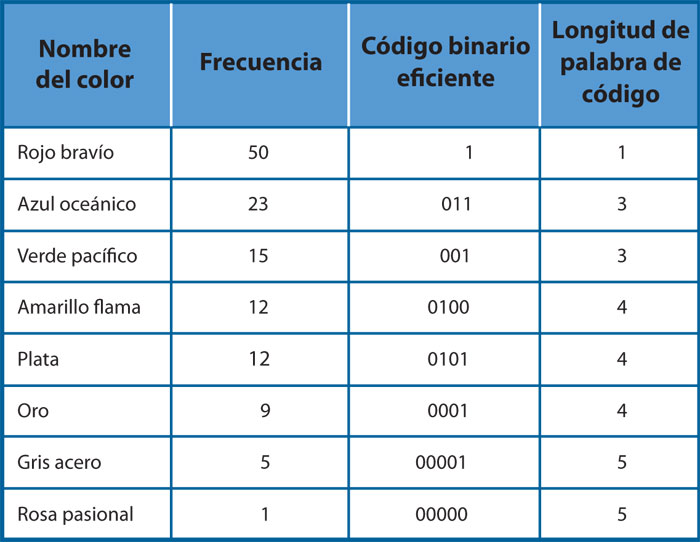
Un ejemplo concreto: una agencia de venta de automóviles desea determinar una codificación eficiente para almacenar los colores de las unidades en su inventario, pero usar los nombres de los colores es poco práctico porque siempre son los mismos y son largos, digamos que se trata de los mostrados en la columna izquierda de la tabla 4. En la segunda columna de la izquierda se muestra el número total de vehículos vendidos de cada color durante los últimos seis meses y constituye un indicador de qué tan frecuente o raro es cada color en el inventario.
En la siguiente columna aparece un código eficiente para representar cada color. Queda fuera del alcance de este texto explicar cómo se obtuvo dicho código, pero lo que hay que notar es que la longitud de las palabras, el número de bits de cada una, está en proporción inversa a la frecuencia del color correspondiente. Si se tuvieran 26 automóviles en el patio de la agencia: 10 rojos, 5 azules, 3 verdes, 3 amarillos, 2 plata, 2 oro, 1 gris y 0 rosas (cantidades que guardan entre sí aproximadamente las proporciones de la tabla), se requerirían 67 bits para codificar los colores de todos. En cambio, si no se supiera nada, si todos los colores fueran igualmente usuales, entonces se requerirían tres bits para cada color, dado que con tres bits se pueden decir exactamente 23 = 8 cosas, igual al número de colores que se tienen. En este caso, para guardar los colores de todos los vehículos del patio se necesitarían 78 bits, puesto que 26 × 3 = 78. Si en vez de los 26 vehículos de la agencia se consideraran los 2 540 que están en el patio de la planta de producción y cuyos números relativos guardan la misma relación de proporcionalidad que se muestra en la tabla, entonces se usarían 6 520 bits en sus colores, mientras que la codificación de tres bits por color requeriría de 7 620.
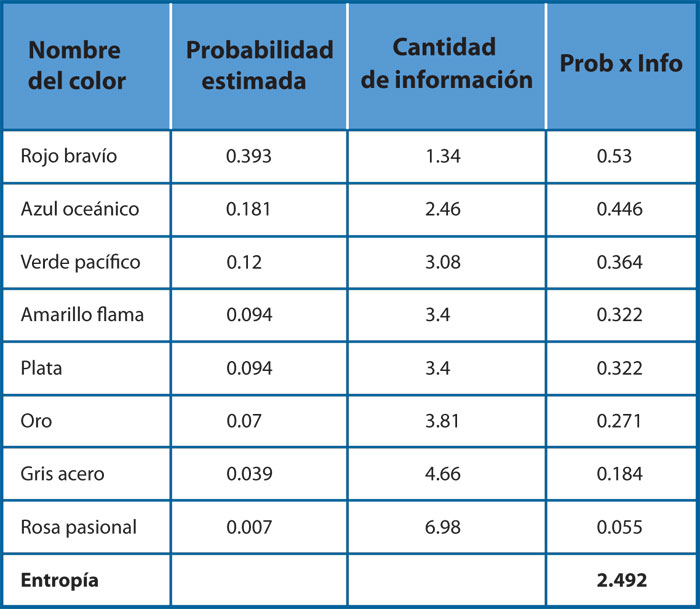
En computación, a la longitud mínima de bits necesarios para codificar (representar) un dato se le denomina cantidad de información y la cantidad promedio de bits necesarios para representar cada uno de los datos de un conjunto se conoce como entropía de información. Éstas son cantidades que se calculan solamente con base en qué tan frecuente o probable es cada uno de los datos de un conjunto, así que pueden ser números fraccionarios. En el ejemplo de los colores de automóviles, la entropía de información del conjunto de colores, con base en su probabilidad (estimada a través de las frecuencias que se muestran), resulta ser 2.49, lo que significa que cada color requiere un código binario que mide en promedio 2.49 bits de longitud. Los datos usados en este cálculo están en la tabla 5.
Curiosidades
Samuel Morse (1791- 1872). Inventor del telégrafo, ideó también el código que lleva su nombre con la misma premisa de eficiencia que hemos mencionado aquí: el código Morse para la letra "E" es sólo un punto; el de la "T" es sólo una raya; el de la "Z", dos rayas y dos puntos. Esto corresponde con la frecuencia con la que esas letras se usan en idioma inglés. Morse quería que su código fuera eficiente para transmitir mensajes en inglés, así que asoció códigos más largos a letras más improbables y más cortos a las más frecuentes: en promedio, en un texto en inglés de 1 000 letras, 127 serán "E", 91 serán "T" y sólo una será "Z".
