Hemos hablado acerca de comprimir y expandir datos sin cambiar la información representada. Pero surgen las siguientes preguntas: ¿qué tanto se puede comprimir?, ¿cómo se sabe si una representación es óptima o, más en general, cómo se puede medir la cantidad de información representada? ¿Cuál es la unidad de medida de la información? Ciertamente, no son los litros ni los gramos. Son los bits. Shannon bien merece el nombre de "padre de la teoría de la información" por haber contestado a estas y muchas otras preguntas relacionadas.
Adivinar el regalo
Arcadio presionó el último dígito del número de Úrsula y cuando escuchó su melodiosa voz le informó que le había comprado un regalo, un disco compacto. Luego le pidió que adivinara de cuál se trataba haciendo preguntas de "sí o no" únicamente.
—A ver... ¿es música popular? —comenzó Úrsula.
—Sí.
—¿Banda?
—No.
—¿Pop?
—Sí.
—¿Nacional?
—No.
—¿Mujer?
—No.
—¿Es de Robbie Williams?
—¡Sí! Eres buena para esto, te tomó sólo seis preguntas.
El juego practicado por Arcadio y Úrsula resulta muy interesante desde el punto de vista computacional, porque nos da la clave acerca de cómo cuantificar la información. Para comprender este concepto pensemos en la siguiente situación: A le pide a U que adivine el número entero en que está pensando en ese momento —puede ser cualquiera entre 0 y 15— haciendo preguntas cuya respuesta sea "sí" o "no".
Es posible preguntarse ahora qué sabe U acerca del número que eligió A. Salvo el hecho de que es algún elemento del conjunto {0, 1, 2, ..., 14, 15}, U no sabe nada. El número elegido por A es completamente arbitrario, elegido de acuerdo con lo que en lenguaje matemático se conoce como probabilidad uniforme. ¿Cómo procedería U a hacer las preguntas para determinar el número que piensa A? Por supuesto, una opción es comenzar preguntando si se trata del 0 y si la respuesta es "sí" se termina el juego, pero si la respuesta es "no" se procedería a preguntar por el 1 y así sucesivamente hasta que la respuesta sea "sí" o hasta que se llegue al 14 (entonces la respuesta obvia sería el 15). Con este procedimiento seguro se resuelve el problema, pero no es eficiente porque en el peor de los casos hay que hacer 15 preguntas. Inclusive en el caso promedio se tendrían que hacer siete preguntas. De hecho, preguntar "¿el número que escogiste es x?" no es eficiente porque el número de preguntas potenciales es siempre el mismo: el tamaño del rango menos uno. Cada respuesta proporciona muy poca información acerca del número elegido; en la mayoría de los casos, sólo indica cuál no es, lo que nos deja con un conjunto de posibilidades igual al que teníamos antes, menos uno.
En cambio, si preguntamos "¿el número es menor que 8?", la respuesta proporciona mucho más información, pues indica en qué mitad de la lista de 16 números está el que se quiere adivinar. Después se puede preguntar por el que se encuentre en la mitad, de la mitad donde se espera que esté el número buscado; eso nos ubica, con sólo dos preguntas, en un conjunto de posibilidades con una cuarta parte del tamaño del conjunto total inicial. Una pregunta más y se estará en una octava parte; luego de la cuarta pregunta se sabe exactamente qué número es el elegido.
En la figura 8 de la siguiente página se observa un despliegue de todas las opciones en función de las respuestas previas. A una estructura como ésta se le denomina árbol de decisión. Cada vez que se recibe una respuesta, se desciende por una de las ramas, la etiquetada con la respuesta recibida. Conforme se avanza, el conjunto de posibilidades es de la mitad del tamaño del conjunto previo.
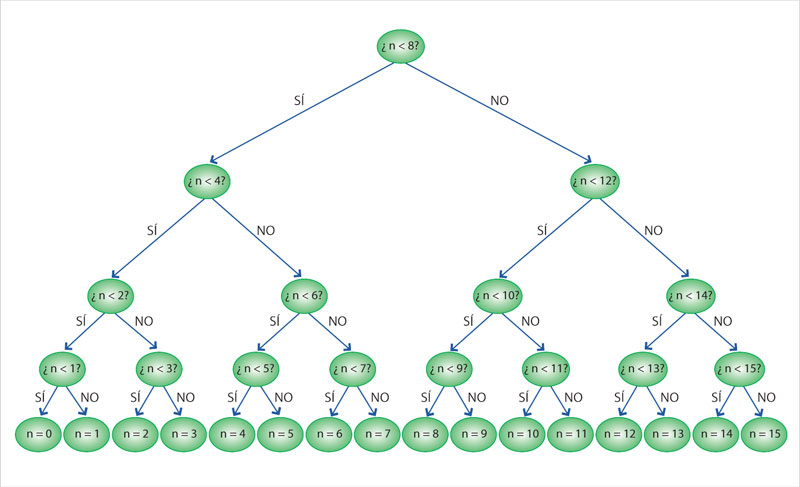
Del análisis del ejemplo se concluye que el número óptimo de preguntas es cuatro. Vale la pena observar que, si se sigue una ruta descendente desde la raíz del árbol hasta una hoja cualquiera, cada arista está etiquetada como "sí" o "no"; de manera que se puede especificar el camino mediante bits, con la secuencia de "sí" y "no" necesaria para llegar a una hoja desde la raíz. Por ejemplo, la ruta para llegar a la hoja "n = 10" es: no, sí, no, sí; la del 6 es sí, no, no, sí. Si se reemplazan los "no" por 1 y los "sí" por 0, se obtiene algo que resulta familiar: la ruta del 10 es 1010 y la del 6 es 0110, que son justamente las representaciones binarias de esos números, como se vio cuando se expresaron los ingredientes de la receta de galletas.
Resumiendo lo anterior, si no hay pistas útiles para poder restringir la búsqueda de un elemento de un conjunto, entonces el número mínimo de preguntas "sí o no" que hay que hacer coincide con la longitud de la expresión binaria mínima necesaria para poder escribir todos los números del conjunto. Si se reflexiona acerca de que cada vez que alguien responde una pregunta está aportando información, entonces se puede decir que, de hecho, la longitud de la expresión binaria mide la cantidad de información necesaria para determinar cada número del conjunto, y es básicamente igual al logaritmo con base 2 del tamaño del conjunto. El tamaño del código usado para representar a los elementos del conjunto indica la cantidad de información contenida en ellos.