¿Cómo representar números, letras, imágenes y sonidos mediante bits? En las siguientes líneas se tratará de argumentar que cualquier cosa es en principio representable mediante bits.
Los números se podrían representar de muchas maneras diferentes usando bits. Como ejemplo, podemos tomar el conjunto de todas las palabras de 0 y 1, y arbitrariamente asignarle a cada número entero una de ellas. A continuación se verá la representación binaria que permite que se puedan manipular y hacer operaciones aritméticas eficientemente.
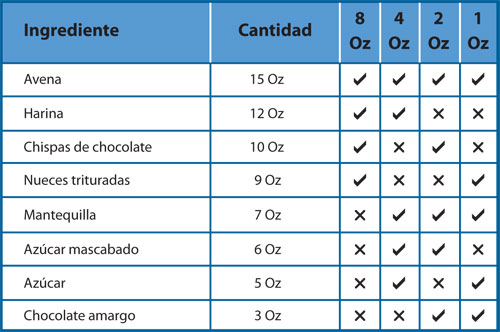
Vale la pena recordar la historia de Úrsula y su madre cocinando galletas. Quedó pendiente ver cómo había hecho Úrsula para medir los ingredientes usando sólo las pocas cucharas medidoras de que disponía: de una, dos, cuatro y ocho onzas. Para recordar las cantidades basta echar una mirada a las dos columnas de la izquierda de la tabla 2.
Lo primero que midió Úrsula fue la avena: 15 onzas. Primero llenó la cuchara de ocho onzas y luego la de cuatro, tenía entonces 8 + 4 = 12 onzas; sólo faltaban tres, que se podrían medir exactamente usando las dos cucharas restantes. Es decir, usando una vez cada cuchara se podían medir las 15 onzas, lo que sin duda era mejor que usar 15 veces la cuchara de una onza, o tres veces la pareja de cuatro y de una. Para medir las 12 onzas de harina sólo tenía que hacer parcialmente lo que había hecho antes, usar la de ocho y la de cuatro. Las 10 onzas de chispas de chocolate se podían medir usando la de ocho y la de dos. En la tabla 2 también se muestran las combinaciones de cucharas que usó Úrsula para medir todas las cantidades en onzas. De hecho, Úrsula se dio cuenta de que cualquier cantidad entera de onzas desde cero hasta 15 podía ser medida usando sólo las cuatro cucharas disponibles a lo más una vez cada una. En general, la estrategia de Úrsula consistió en usar la cuchara más grande posible, cuya capacidad fuera menor o igual a la cantidad que necesitaba medir. Si era igual, el asunto estaba resuelto, si no, entonces quedaba algo por medir y procedía igual, eligiendo la cuchara con la mayor capacidad posible que no excediera la cantidad necesaria.
Para resolver el problema de medir las cantidades necesarias de cada ingrediente usando sólo las cucharas disponibles, Úrsula recurrió a representar cada una de las cantidades, de manera no muy distinta a la que usamos cotidianamente. Desde la enseñanza elemental se aprende que el número 4649, por ejemplo, está compuesto por: cuatro unidades de millar, seis centenas, cuatro decenas y nueve unidades o, lo que es lo mismo:
4649 = 4 × 1000 + 6 × 100 + 4 × 10 + 9 = 4 × 103 + 6 × 102 + 4 × 101 + 9 × 100
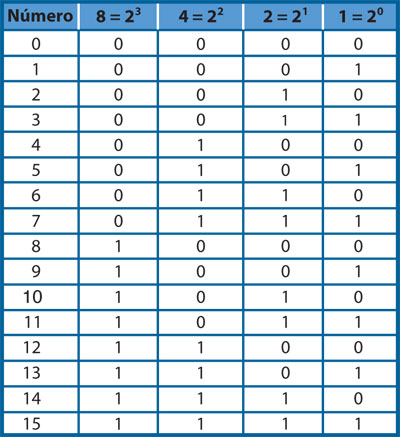
Recordemos que cualquier número elevado a la potencia cero vale 1; es decir, el valor de cada dígito del número se multiplica por una potencia de 10. Esta característica del sistema numérico usual es compartida por todos los sistemas llamados posicionales. En ellos, el valor de un número está siempre vinculado con lo que se denomina la base del sistema. En la vida cotidiana usamos el 10 como base, por eso se dice que es un sistema decimal o de base 10. Sin saberlo, Úrsula se dio cuenta de esto. Cualquier cantidad entre 0 y 15 onzas puede ser medida con las cucharas que tenía porque a éstas les cabía exactamente una potencia de 2. De hecho, Úrsula entró en contacto con el sistema binario o con base 2. En este sistema, los únicos dígitos posibles son el 0 y el 1, los dígitos binarios, o sea el ideal para usarse en una computadora, con bits. En la tabla 3 se puede ver cómo se expresa cualquier entero en el rango mencionado, reemplazando las "palomas" por unos y los "taches" por ceros.
Curiosidades
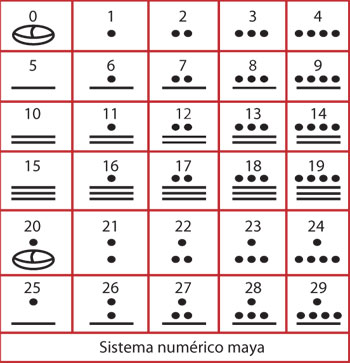
No todos los sistemas numéricos que ha usado la humanidad a lo largo de la historia han sido posicionales. Los sistemas, como el romano o el egipcio, en los que un símbolo vale siempre lo mismo sin importar su posición dentro del número, se denominan aditivos. Algunos pueblos, como los antiguos celtas, los mayas y los indios, usaron sistemas posicionales; los primeros dos tomaron al 20 como base del sistema, mientras que los últimos prefirieron el 10. Nuestro actual sistema proviene del que usaban los indios y, posteriormente, los árabes, por lo que solemos llamarlo indoarábigo.
Así pues, el 11 en el sistema decimal (al que denotaremos como 1110) se escribe en binario como 1011 (o para ser consistentes con nuestra notación10112) porque:
10112 = 1 × 23 + 0 × 22
+ 1 × 21 + 1 × 20 = 1 × 8
+ 1 × 4 + 1 × 2 + 1 × 1 = 8
+ 0 + 2 + 1 = 1110