Ahora se utilizará una estructura gráfica para generar un laberinto perfecto y, más adelante, se usará la misma estructura y un algoritmo importante para encontrar la salida. ¿Qué hace fáciles a los laberintos perfectos? Que todas las posiciones o celdas se pueden ver como un cuadrado con dos posibles paredes: derecha y abajo. El marco del laberinto se convierte en paredes para todas las celdas en las orillas. Entonces, la estrategia de construcción es muy sencilla:
1] Seleccionar una celda como entrada y otra como salida del laberinto. Por convención, la entrada será la celda en la esquina superior izquierda y la salida en la esquina inferior derecha.
2] Al inicio, todas las paredes del laberinto están puestas. Es decir, no existe ningún camino, cada celda del laberinto tiene cuatro paredes.
3] Ubicarse en la entrada (funciona también si elegimos una celda aleatoria).
4] Localizar de manera aleatoria una celda vecina no visitada aún.
5] Si existe tal celda vecina, moverse hacia ella, tirando la pared entre las celdas. Si no hay celda vecina, regresar a la celda anterior.
6] Repetir los pasos 4 y 5 hasta que se hayan visitado todas las celdas del laberinto.
Los pasos 3 a 6 constituyen un algoritmo muy famoso de exploración general de gráficas, conocido como búsqueda a profundidad (dfs, por sus siglas en inglés). Una vez más, se va a descomponer el problema completo en varios problemas menores. Se comenzará por el procedimiento principal: crea-laberinto y las variables globales para almacenar el laberinto, el número de renglones y el número de columnas.
(define renglones 0)
(define columnas 0)
(define laberinto #f)
(define-struct celda (x y derecha abajo visitada))
(define (crea-laberinto rens cols)
(let ((lab (make-vector rens))
(i 0))
(while (< i rens)
(let ((columna (make-vector cols))
(j 0))
(while (< j cols)
(vector-set! columna j (make-celda i j #t #t #f))
(set! j (+ j 1)))
(vector-set! lab i columna))
(set! i (+ i 1)))
;; Se almacena la información en las variables globales:
(set! renglones rens)
(set! columnas cols)
(set! laberinto lab)
;; Ahora generan las rutas:
(crea-rutas (vector-ref (vector-ref laberinto 0) 0) #f)))
¿Qué puntos de la estrategia se han definido? 1, 2 y 3, por supuesto. Los dos ciclos while anidados permiten recorrer todas las celdas del laberinto e inicializar cada una, de modo que tengan ambas paredes y estén marcadas como no visitadas. La estructura celda almacena varias cosas: su posición en el laberinto (cuadrícula), si las paredes derecha e inferior aún están de pie y, finalmente, un campo que se llamará visitada, que se utilizará en el algoritmo de búsqueda a profundidad para saber si el algoritmo ya pasó por esta celda. La siguiente parte importante es el procedimiento crea-rutas, implementado por los puntos 3 al 6:
(define (crea-rutas celda dir)
;; Primero, se marca la celda actual como visitada.
(set-celda-visitada! celda #t)
;; Se verifica la dirección y se tira la pared en esa dirección.
(if dir
(tira-pared celda dir))
;; Después, se recorren las posibles direcciones, tirando paredes.
(dfs celda (posibles-direcciones (celda-x celda) (celda-y celda))))
(define (dfs celda direcciones)
(if (null? direcciones)
'()
(let ((vecino (obtener-vecino celda (car direcciones))))
(if (not (celda-visitada vecino))
;; Vecino no visitado, se recorre primero:
(crea-rutas vecino (car direcciones)))
;; Y luego se recorren las demás direcciones (backtrack).
(dfs celda (rest direcciones)))))
Los comentarios explican la función de cada parte de los procedimientos. Sin embargo, un concepto nuevo e importante aquí es que crea-rutas y dfs son procedimientos mutuamente recursivos; es decir, hacemos llamadas entre ellos conforme avanzamos. Aquí se explica la lógica de esto:
• Crea-rutas se encarga de marcar una celda, que nunca había sido visitada antes, como visitada. Después, localiza todas las posibles direcciones en las que nos podemos mover desde esta celda y llama a dfs para recorrer tales rutas.
• dfs, como ya se dijo, recorre todas las direcciones posibles desde la celda actual. Sin embargo, cuando selecciona de manera aleatoria una celda vecina que no ha sido visitada… ¿qué hacer con una celda nunca antes visitada? ¡Exacto!, se envía la celda a crea-rutas.
Las definiciones auxiliares que se verán a continuación cumplen funciones importantes y se puede pensar en ellas como pequeños bloques de construcción: posibles-direcciones, tira-paredes y obtener-vecino. La segunda y tercera son muy sencillas. Continuando con la tercera: ¿cómo obtener el vecino de una celda en una dirección determinada? Si es el vecino a la izquierda, se resta 1 a la columna de la celda actual; por ejemplo, si se está en la celda (5,3), el vecino de la izquierda está en el mismo renglón, 5, pero en la columna anterior, o sea, 2. Y algo similar para las demás direcciones. Obsérvese con detalle:
(define (obtener-vecino celda dir)
(cond ((eq? dir 'izquierda)
(vector-ref
(vector-ref laberinto (celda-x celda))
(- (celda-y celda) 1)))
((eq? dir 'derecha)
(vector-ref
(vector-ref laberinto (celda-x celda))
(+ (celda-y celda) 1)))
((eq? dir 'arriba)
(vector-ref
(vector-ref laberinto (- (celda-x celda) 1))
(celda-y celda)))
(else
(vector-ref
(vector-ref laberinto (+ (celda-x celda) 1))
(celda-y celda)))))
¿Cómo tirar una pared? Se asigna #f a la pared en cuestión. Hay un par de puntos que considerar: primero, recuérdese que cada celda se encarga de su pared derecha y su pared inferior; segundo, se mueve a la celda vecina y desde ahí se tira la pared. Por ejemplo, supóngase que se está en la posición (3,3) y se hace un movimiento hacia la derecha, a la celda ubicada en (3,4). ¿Qué pared se debe tirar? La pared entre las columnas 3 y 4 en el renglón 3. A continuación se presenta la definición:
(define (tira-pared celda dir)
(cond ((eq? dir 'izquierda)
(set-celda-derecha! celda #f))
((eq? dir 'derecha)
(set-celda-derecha! (obtener-vecino celda
'izquierda) #f))
(eq? dir 'arriba)
(set-celda-abajo! celda #f))
(else
(set-celda-abajo! (obtener-vecino celda
'arriba) #f))))
Finalmente, posibles-direcciones es un procedimiento con un pequeño truco, ya que se necesita seleccionar de manera aleatoria a los vecinos. Entonces, lo que se hace primero es generar las direcciones válidas desde la posición actual; por ejemplo, en la posición (0,0), las únicas direcciones válidas son hacia la derecha y abajo, pero en (1,1), es posible moverse hacia las cuatro direcciones. Aquí está la primera parte:
(define (posibles-direcciones x y)
(random-list
(filter symbol?
(list (and (> y 0) 'izquierda)
(and (< y (- columnas 1)) 'derecha)
(and (> x 0) 'arriba)
(and (< x (- renglones 1)) 'abajo)))))
Y ahora, como se quieren reordenar esas direcciones de manera aleatoria, se llama a random-list, que genera un número aleatorio entre 0 y el número de direcciones posibles y con ese valor rota la lista, para darle un orden distinto. Por ejemplo, si la lista de direcciones posibles es '(izquierda derecha abajo) y el número aleatorio es 2, es decir, la última posición de la lista, entonces random-list regresa '(abajo izquierda derecha). Este procedimiento da variedad a los laberintos, lucen más bellos y complicados.
(define (random-list L)
(let* ((len (length L))
(primera (random len))
(i 0)
(resultado '()))
(while (< i len)
(set! resultado
(append (list
(list-ref L (módulo (+ primera i) len)))
resultado))
(set! i (+ i 1)))
resultado))
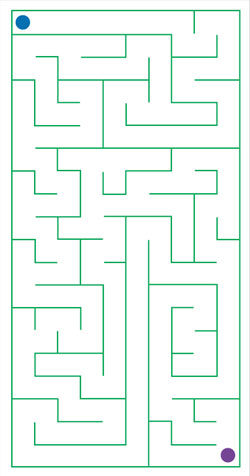
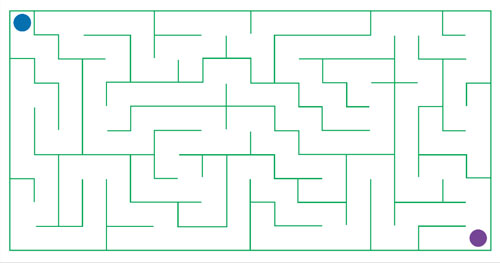
A continuación se muestran algunos ejemplos del programa. Estas versiones gráficas, así como el código que las genera vienen en el DVD que acompaña este libro. Al abrir el archivo "laberinto" en DrScheme y hacer clic en Ejecutar, aparecerá un diálogo que solicita el número de renglones y columnas del laberinto. Aquí se muestran uno de 10 × 20 y otro de 20 × 10, donde el punto azul indica la entrada y el morado la salida del laberinto.