Las listas son estructuras abstractas de datos muy útiles y, como se puede apreciar, son sumamente versátiles: han sido utilizadas para almacenar números, símbolos, etcétera. Ahora se presentarán otras estructuras de datos, mismas que se usarán para programar algunos ejemplos.
Un vector es una estructura de datos en la cual se puede acceder a cualquier elemento individual a través de un número entero o índice y, lo más importante, en tiempo constante. En una lista, acceder a un elemento particular implica recorrer la lista hasta encontrarlo, lo que hace atractivos a los vectores para ciertas aplicaciones. En la siguiente tabla se muestran las operaciones principales de esta estructura abstracta de datos.

¿Con las primitivas para vectores se puede definir una matriz bidimensional, por ejemplo de 5 × 5 elementos? Sí, se puede crear un vector de tamaño cinco y después utilizar vector-set! y asignar otros vectores en cada posición, ésta es una tarea fácil para un ciclo:
(define i 0)
(define v (make-vector 5))
(while (< i 5)
(vector-set! v i (make-vector 5))
(set! i (+ i 1)))
Al final, v es una matriz de 5 x 5 elementos, así que es posible almacenar y recuperar objetos de cualquiera de sus 25 posiciones, por ejemplo:
> v
#5(#5(0) #5(0) #5(0) #5(0) #5(0))
> (vector-set! (vector-ref v 2) 0 "Una cadena")
> (vector-set! (vector-ref v 2) 1 2500)
> v
#5(#5(0) #5(0) #5("Una cadena" 2500 0) #5(0) #5(0))
> (vector-ref (vector-ref v 2) 0)
"Una cadena"
> (vector-ref v 2)
#5("Una cadena" 2500 0)
Como se observa, la notación #N y luego una lista son utilizadas por DrScheme para indicar que se trata de un arreglo de tamaño N. La lista que sigue está conformada por los elementos del arreglo y si todas las posiciones tienen el mismo valor, sólo repite dicho valor. Así, #5(0) se traduce en un arreglo de cinco posiciones, cada una con un cero. En los ejemplos, v es un vector de tamaño cinco pero cada elemento del arreglo es a su vez otro arreglo distinto de cinco posiciones cada uno. Un ejemplo interesante con vectores es el ordenamiento por selección que se definió en el capítulo anterior:
1] Encontrar el menor elemento en la lista.
2] Intercambiarlo con el primero de la lista.
3] Repetir 1 y 2 para el resto de la lista empezando en la segunda posición.
Sólo que, en lugar de una lista, se va a utilizar un vector. En el DVD que acompaña este libro se encuentra una versión con listas; sin embargo, es un poco más complicada por diferencias fundamentales entre las estructuras lista y vector. Siguiendo el principio de construcción en bloques, es claro que el primer paso constituye en sí mismo un procedimiento y que se pueden juntar 2 y 3 en un segundo procedimiento que resuelve el problema. Aquí está la versión en código:
;; contrato: v[vector de números] -> vector ordenado
;; propósito: ordenar el vector de manera ascendente,
;; utilizando el algoritmo por selección.
;; ejemplo: (ordenar #(5 4 3 2 1)) debe producir #(1 2 3 4 5)
;; definición:
(define (ordenar v)
(ordenar-por-inserción v 0 (vector-length v)))
(define (ordenar-por-inserción v desde hasta)
(if (= desde hasta)
v ;; Hemos terminado, v está ordenado
(let ((menor (posición-del-menor v desde (+ desde 1) hasta))
(primero (vector-ref v desde)))
;; Primero, ponemos el menor en su posición:
(vector-set! v desde (vector-ref v menor))
;; Y al número que estaba ahí, en la posición del menor:
(vector-set! v menor primero)
;; Y ordenamos el resto del vector:
(ordenar-por-inserción v (+ desde 1) hasta))))
La primera definición, ordenar, facilita llamar al procedimiento que lleva a cabo el ordenamiento, ordenar-por-inserción. Los pasos 2 y 3 del algoritmo de ordenamiento arriba, se definen en el procedimiento auxiliar, ordenar-por-inserción, que recibe el vector y algunos datos fijos acerca del vector: desde y hasta. En el primer paso desde vale 0 y se aumenta en 1 conforme avanza el programa, mientras que hasta7 nunca cambia y es el tamaño del vector. El paso 1 del algoritmo lo realiza el procedimiento posición-del-menor:
(define (posición-del-menor v menor sig v-len)
(cond ((= sig v-len) menor) ;; última posición
((< (vector-ref v sig) (vector-ref v menor))
;; nuevo menor en la posición "sig"
(posición-del-menor v sig (+ sig 1) v-len))
(else
;; el número en "menor", sigue siendo
el más pequeño
(posición-del-menor v menor (+ sig 1) v-len))))
Este procedimiento encuentra al menor en el vector, entre las posiciones menor y v-len, que es la longitud del vector. Por la recursividad en ordenar-por-inserción, el menor va creciendo conforme se ordena el vector. A continuación unas pruebas:
> (ordenar #(1 2 3 4 5 4 3 2 1))
#(1 1 2 2 3 3 4 4 5)
> (ordenar #(100 80 50 60 10))
#(10 50 60 80 100)
Curiosidades
En la película El cubo (1997), un hombre despierta completamente solo dentro de un cuarto en forma de cubo. No tiene idea de dónde se encuentra ni cómo llegó ahí. El cubo es perfecto; en cada uno de sus seis lados hay una compuerta para salir de éste. Al abrir una de las compuertas, el hombre se da cuenta de que ésta lo lleva a otro cubo idéntico al primero. Paulatinamente, se percata de que está encerrado en un laberinto gigantesco en forma de cubos interconectados, que además se mueven. El hombre debe encontrar la salida o morir, ya que los cubos no tienen agua ni comida. Éste es un ejemplo de un laberinto tridimensional móvil, entre los tantos laberintos dificilísimos de resolver que se han inventado. Hay más ejemplos en <http:// www.clickmazes.com/ mazes/ixmaze.htm>.
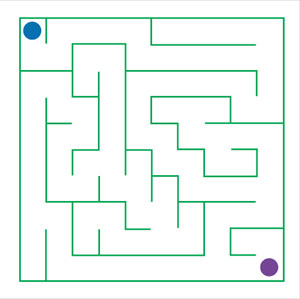
Existen muchos tipos de laberinto. En computación se estudia la creación de laberintos y cómo encontrar la salida. La relación con gráficas es íntima debido a que la forma de los caminos en sí, dentro de un laberinto, no es importante para encontrar la salida; lo que importa es qué caminos existen y de qué manera están interconectados. Algunos son más difíciles de resolver que otros, pero aquí la discusión se centrará en un tipo particular conocido como laberinto perfecto. Este tipo de laberintos debe su nombre a que dos posiciones en el laberinto (entrada-salida) están conectadas entre sí por un camino único (figura 9).
Un laberinto perfecto no tiene secciones inaccesibles, no tiene rutas circulares y no tiene áreas abiertas.