Se han revisado ya varios procedimientos para construir y desarmar listas, pero qué sucede si se quiere modificar el contenido de una lista. Con lo que se conoce hasta ahora, es posible recorrer una lista para ordenarla y crear una nueva, lo cual es una buena opción para listas pequeñas. En caso de listas grandes se desperdicia mucha memoria al duplicarlas, así que se mostrará algo equivalente a la asignación general, set-first! y setrest! que actualizan, de manera destructiva, el primer elemento y el resto (todos menos el primero) de una lista, respectivamente. Existe un procedimiento más que se llama list-set! que asigna un valor a una posición particular, por ejemplo:
> (define lista '(50 20 5 12 35))
> (list-set! lista 2 1000)
> lista
(50 20 1000 12 35)
Se recordará que en el tema 2 se plantearon varios algoritmos de ordenamiento que funcionaban con listas de números. ¿Qué tal si se programa uno de ellos? Por ejemplo, el ordenamiento por combinación, mergesort.
En el tema anterior se definió el siguiente algoritmo:
OrdenaM (L)
Si longitud de L es 1
Regresa L
De otro modo
Divide L en 2 del mismo tamaño (aproximadamente), L1 y L2
OrdenaM(L1)
OrdenaM(L2)
Mezcla(L1,L2)
Y a continuación se muestra la versión en Scheme, que es idéntica al algoritmo descrito arriba:
;; contrato: L[lista de números] -> lista ordenada
;; propósito: ordenar una lista de números, L, de menor a mayor.
;; ejemplo: (mergesort '(5 4 3 2 1)) debe producir (1 2 3 4 5)
;; definición:
(define (mergesort L)
if (<= (length L) 1)
L
let ((mitad (quotient (length L) 2)))
merge
mergesort (list-head L mitad))
mergesort (list-tail L mitad))))))
Hay algunos detalles que aclarar; por ejemplo, ¿cuál es la mitad de una lista? Eso es fácil, es la longitud de la lista dividida entre 2. Sin embargo, si la lista es de longitud impar esto produciría un número racional; por ejemplo, si la lista es de longitud 5, la mitad es 2.5. Por este motivo se utiliza quotient en lugar de /, sólo se mantiene el cociente de la división: (quotient 5 2) regresa 2.
Hay otros procedimientos que no se habían visto antes, pero son muy sencillos: (list-head L N) regresa los primeros N elementos de la lista L y (list-tail L N) se salta los primeros N elementos y regresa el resto de la lista L. La primera, list-head, no es una primitiva de Scheme, por eso se define aquí, pero la segunda sí es primitiva.
(define (list-head L hasta)
(if (zero? hasta)
'()
(cons (car L) (list-head (rest L) (- hasta 1)))))
Finalmente, se obtendrá el procedimiento que mezcla las dos sublistas en el algoritmo. La idea esencial es la siguiente: se coloca un dedo índice en la primera posición de cada lista y se comparan; el menor de ellos se pone en el resultado y se avanza el dedo (recortando el problema) en esa lista y se vuelve a intentar. En la figura 6 se muestra un ejemplo con dos listas ordenadas (1, 3, 4) y (2, 5, 6); los dedos índices están marcados por las flechas al inicio de cada lista. Entonces se comparan 1 con 2 y el menor se lleva al resultado, como se muestra en la figura 7 y avanza el índice izquierdo.
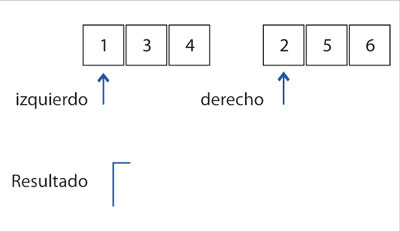
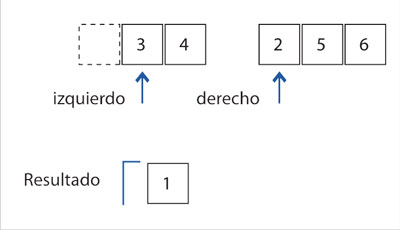
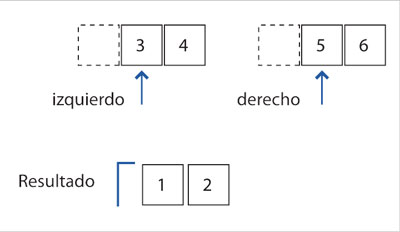
Después de avanzar el índice izquierdo, se compara 4 con 5 y se mueve el 4 al resultado. Cuando avanza el índice izquierdo se puede notar que la lista ya se acabó. En ese momento ya no hay más comparaciones que hacer; el resto de los elementos en la otra lista, la derecha, se agregan al final del resultado. El código es:
(define (merge L1 L2)
(cond ((empty? L1) L2)
((empty? L2) L1)
((< (car L1) (car L2))
(cons (car L1) (merge (rest L1) L2)))
(else
(cons (car L2) (merge L1 (rest L2))))))
A continuación se presentan algunas pruebas del procedimiento:
> (mergesort '(5 4 3 2 1))
(1 2 3 4 5)
> (mergesort '(20 3 17 4 5 8 1 65 19 9))
(1 3 4 5 8 9 17 19 20 65)