Es usual querer conservar valores intermedios durante un cómputo; para lograrlo, Scheme ofrece un mecanismo que permite realizar asignaciones de un valor a una variable.
La primera parte que consiste en definir una variable ya es conocida y se realiza igual que con las definiciones de procedimientos, es decir, con define:
(define variable valor-inicial)
Una vez que la variable existe, se puede modificar su valor con la forma especial set!; aquí, al igual que en los predicados, el signo de admiración se utiliza por convención para señalar que en adelante modifica el valor que se le había dado al argumento. La asignación se debe usar con cuidado porque en su presencia el modelo de sustitución para las evaluaciones no funciona. Así se utiliza set!:
(set! variable nuevo-valor)
Ahora sí, todo está listo. Utilizando set! se va a escribir el procedimiento factorial para que modifique la variable que guarda el resultado intermedio:
;; Definición:
(define contador 1)
(define resultado-parcial 1)
(define (factorial n)
(while (<= contador n)
(set! resultado-parcial (* contador resultado-parcial))
(set! contador (+ contador 1))
)
;; regresamos el resultado
resultado-parcial)
¿Por qué no se selecciona cero como el valor inicial del resultado-parcial? ¿Cuánto vale el factorial de 0?
Como se puede notar, se modificó también el contador al incrementar un 1 y con esto, efectivamente, se logra avanzar de uno en uno el contador desde 1 hasta n. El programa calcula de manera correcta el factorial de un número entero positivo si se ejecuta una sola vez. Este diseño no es bueno debido a la utilización de las variables globales contador y resultado-parcial que no están asociadas únicamente al procedimiento factorial para el cual están pensadas. Por eso no siempre funciona bien si se ejecuta repetidamente.
Se ha visto cómo hacer asignaciones y a partir de esto crear variables globales con define y set!; sin embargo, la idea de las variables globales es permitir definiciones que tengan sentido por sí mismas. En el ejemplo de factorial citado arriba, había una variable contador y otra resultado-parcial, que sólo tenían sentido en el procedimiento, por ello se aclara que era una mala práctica de programación. Ahora se utiliza una forma local de asignación llamada let, cuya forma general es:
(let [(var1 valor1)
(var2 valor2)
...
(varN valorN)]
expresiones)
Ahora se puede reescribir el procedimiento factorial, en estilo imperativo, pero con variables locales:
(define (factorial n)
(let ((contador 1)
(resultado-parcial 1))
(while (<= contador n)
(set! resultado-parcial (* contador resultado-parcial))
(set! contador (+ contador 1))
)
;; regresamos el resultado
resultado-parcial))
Curiosidades
El paradigma de programación, como el que se usa en el caso del factorial con contadores, recibe el nombre de programación imperativa; en ella se hace un uso extenso de asignaciones.
lo cual, además de calcular el factorial correctamente siempre que se ejecute, es más claro, y los contadores que sólo tienen sentido para el procedimiento son invisibles desde fuera.
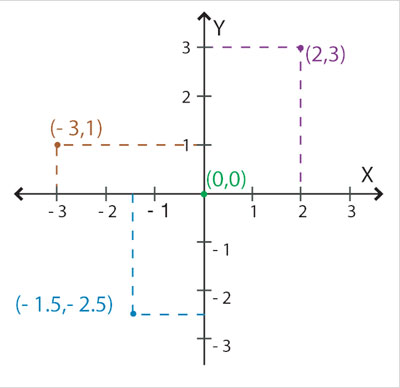
A continuación se presentará otro ejemplo que aclara el uso de let. Recuérdese la manera de calcular la distancia entre dos puntos en el plano. Por ejemplo, la distancia entre los puntos (-3,1) y (2,3), los puntos café y verde, respectivamente, en la figura 5, se calcula de la siguiente forma:
d=√(-3-2)2 + (1-3)2
Es decir, se restan las coordenadas X, luego las Y; se elevan al cuadrado esas cantidades, se suman y se saca raíz cuadrada de todo. Es muy sencillo, así que aquí se muestra la versión con receta de diseño:
;; Contrato: distancia número número número número -> número
;; Propósito: Calcular la distancia entre dos puntos cualesquiera en el plano.
;; Ejemplo: (distancia -3 1 2 3) debe producir 5.38
;; Definición
(define (distancia x1 y1 x2 y2)
(sqrt (+ (* (- x1 x2) (- x1 x2))
(* (- y1 y2) (- y1 y2)))))
;; Pruebas:
(distancia -3 1 2 3)
Como puede notarse, se repiten dos veces las restas: (- x1 x2) y (- y1 y2) y éste es un caso típico para utilizar let, como una especie de abreviatura:
(define (distancia x1 y1 x2 y2)
(let ((dif-x (- x1 x2))
(dif-y (- y1 y2)))
(sqrt (+ (* dif-x dif-x)
(* dif-y dif-y)))))
En estos casos, además de mejorar la visibilidad del procedimiento, también se reduce la posibilidad de cometer errores al escribir menos veces cada término, así el intérprete puede ejecutar más rápido el procedimiento. Por ejemplo, en lugar de calcular cuatro restas, DrScheme sólo calcula dos restas y utiliza los resultados de éstas las cuatro veces que son requeridas.
En el capítulo anterior se analizó el problema de encontrar los puntos más cercanos en un conjunto de n puntos, y el algoritmo de fuerza bruta que se definió es:
Para cada pareja de puntos x, y:
Sea d la distancia de x a y
Si d es menor a dmin, la menor distancia vista hasta ahora,
Sea dmin igual a d
¿Cómo escribir eso en Scheme? Ya se sabe calcular la distancia entre dos puntos, pero ¿cómo representar un conjunto de puntos?