Armados con las herramientas necesarias para esta travesía y recorrer los fundamentos de la programación, ¡manos a la obra! Para dar una idea clara de qué se espera, se verá cómo funciona el ambiente de trabajo, comenzando por el intérprete de Scheme que se encuentra en la ventana de interacciones de DrScheme.
Cada vez que se escribe algo como una expresión y se ingresa al intérprete con entrar, éste responde imprimiendo en pantalla el resultado de su evaluación. Existen muchos tipos de expresiones, de las cuales las más sencillas son los números. En la figura 3 se muestran algunas interacciones muy sencillas con números.
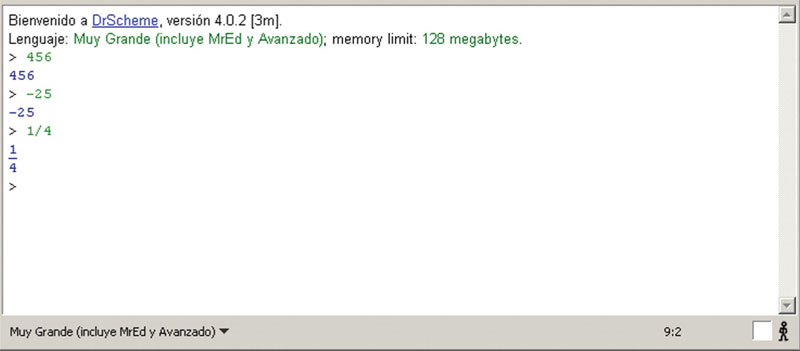
Nótese que el intérprete regresa (marcado en azul) exactamente el mismo valor; esto se debe a que los números y algunos otros elementos son autoevaluados, es decir, que su valor de regreso es el mismo que el de su representación.
Por convención y espacio, a partir de este momento no se mostrarán las imágenes de DrScheme, sino que se indicarán directamente las expresiones, procedimientos o programas, y se marcarán con azul las evaluaciones o los mensajes que imprima DrScheme.
Hay varios procedimientos primitivos, o sea que ya están integrados al sistema para operar con números: + (suma), - (resta), / (división), * (multiplicación), entre otros. Para realizar operaciones con estas primitivas se utiliza la notación prefija:
(+ 2 3) (- 5 1) (* 3 4) (/ 25 3)
Todas estas formas también son expresiones, por lo que se puede utilizar el intérprete como cualquier calculadora de bolsillo y, por supuesto, hará lo correcto, por ejemplo:
> (+ 2 3)
5
Un número es una expresión compuesta. Las expresiones compuestas serán las más comunes y no hay límite en las combinaciones de expresiones que se pueden realizar. Por ejemplo, las siguientes son expresiones válidas:
(+ (- 5 1) 4) (/ (+ 1 2) (* 3 4))
La primera regresa 8 y la segunda ¼. ¿Cómo funciona esta evaluación? Para explicarlo se usará un sencillo modelo de sustitución de expresiones. Así, la primera expresión indica:
> (+ (- 5 1) 4)
> (+ 4 4)
8
Lo que sucedió es que primero se evalúan las expresiones internas y se sustituyen en la versión original. Las sustituciones se realizan de adentro hacia afuera; primero, las más internas y así sucesivamente hasta obtener un resultado. En general, todas las expresiones en Scheme tienen la forma
operación A … B)>
lo que facilita saber qué tiene que evaluarse primero. Si todos los argumentos A…B son números, se puede realizar la operación y obtener un valor. Si no es así, entonces primero se evalúa A…B (en cualquier orden) y se sustituyen sus resultados en la expresión original. Con una expresión escrita de la manera familiar, como: "5 + 3 * 2" no sucede lo mismo. ¿Cómo saber si primero se debe sumar y luego multiplicar para obtener 16 de resultado? O hacerlo al revés, y obtener 11 como resultado.
Se sabe debido a la convención de dar siempre preferencia al * y ejecutarlo antes del +. La versión en Scheme para obtener el mismo resultado es: (+ 5 (* 3 2)). En la manera familiar de escribir sería impráctico tener que definir una precedencia entre las operaciones y, además, a veces se requiere que las operaciones se evalúen en un orden diferente al convencional, así que de todos modos se termina por usar paréntesis para indicar el orden deseado de evaluación, como en (5 + 3) * 2.
Además de las operaciones básicas, como suma y multiplicación, Scheme también soporta varias operaciones matemáticas avanzadas: (sqrt n), raíz cuadrada de n; (exp n m), exponencial nm; (log n), el logaritmo natural de n; (sin n), que calcula el seno de n radianes. Existen varias operaciones aritméticas más y, en general, una buena forma de saber si DrScheme las soporta o no es escribir un ejemplo en la ventana de interacciones.
Una característica que se utilizará frecuentemente es la habilidad del intérprete para ignorar espacios blancos; así, por ejemplo, la expresión:
> (- (+ 2 (* 12 (/ (expt 2 5) 2))) 3)
que se evalúa 191, puede escribirse como:
> (- (+ 2
(* 12)
(/ (expt 2 5)
2)
)
)
3)
lo que facilita la lectura y comprensión de la expresión.
Al igual que en álgebra, en programación se utilizan variables como marcadores para cantidades que no se conocen. Por ejemplo, el área de un círculo de radio r está dada por: 3.14 × r 2. En esta fórmula, r es un marcador para cualquier número positivo. Estos marcadores se conocen como variables.
Al programar, una expresión que contiene variables se convierte en una regla que indica cómo calcular una operación determinada cuando obtenemos un valor para las variables. Un procedimiento o programa es una de esas reglas. Así, se define un procedimiento para calcular el área de un círculo:
(define (área-círculo r)
(* 3.14 (* r r)))
Más aún, se puede definir también la variable pi con su valor usual:
(define pi 3.14)
y entonces reescribir el método original para que utilice esta variable:
(define (área-círculo r)
(* pi (* r r)))
Ahora se puede aplicar o utilizar esta nueva definición de la misma manera en que se usan las primitivas. Nótese que la definición misma del procedimiento indica cómo se debe utilizar: (área-círculo r). Por ejemplo:
28.26
En este ejemplo, al número 3 se le denomina el argumento del procedimiento. En contraste, a la r se le llama el parámetro.
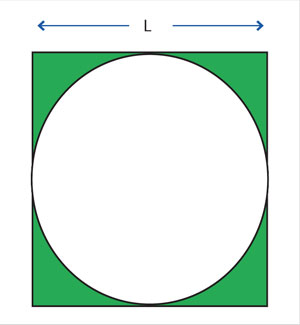
Se puede utilizar el procedimiento área-círculo para construir procedimientos más complicados, como ocurrió con la primitiva *. Un buen intento es el siguiente: hacer un programa que calcule el área sombreada en la figura 4.
El procedimiento para determinar el área del círculo fue muy sencillo. Se ve más complicado, pero sólo se tiene que calcular el área del cuadrado y restarle el área del círculo. Es momento de utilizar la receta de diseño; son seis sencillos pasos:
;; Contrato: área-cuadrado-círculo: L[número] -> número
;; Propósito: calcular el área que se obtiene de restar
el área del
;; círculo a la del cuadrado. Recibe el tamaño L de un lado;; del cuadrado.
;; Ejemplo: (área-cuadrado-círculo 5) debe producir 5.375
;; Definición:
(define (área-cuadrado-círculo L
(- (área-cuadrado L)
(área-círculo (/ L 2))))
;; Pruebas:
(área-cuadrado-círculo 5)
Hay muchos detalles que deben explicarse aquí:
1] Todo se escribe en la ventana de definiciones de DrScheme.
2] Las líneas que empiezan con ";" son comentarios que ignora el intérprete de Scheme.
3] Ya se conoce el área-círculo, pero se utiliza además área-cuadrado. ¿Cuál es el procedimiento? Todavía no se ha definido. Se podría dejar como ejercicio, pero es muy sencillo: el área de un cuadrado de lado L es L 2. Adelante se encuentra la definición.
4] ¿Por qué utilizar (/ L 2) como radio del círculo?
5] Algunos pasos de la receta no son explícitos, por ejemplo el primero, el análisis del problema. No se hizo mayor énfasis, porque ya se indicó que la resta de las áreas de las figuras determina el área sombreada y eso funciona como análisis. Se agregó, sin embargo, una primera sección llamada contrato, cuyo nombre se debe a que todos los procedimientos consumen y "regresan" algo, en este caso números. La L entrada representa la longitud del lado del cuadrado (y ya se sabe que la mitad de eso es el radio del círculo) y la salida representa el área sombreada.
Ésta es la definición que faltó para determinar el área de un cuadrado. Como se señaló en el tema 2, se conoce como
(define (área-cuadrado L)
(* L L))
Hay otras formas de resolver el mismo problema; por ejemplo, en lugar de utilizar área-círculo se puede insertar (* pi (* (/ L 2) (/ L 2))), que calcula el área del círculo. Sin embargo, como es fácil imaginar, luciría más complejo el procedimiento completo. El uso de área-círculo y área-cuadrado agrega claridad, hace más fácil el mantenimiento y corrige errores en el procedimiento. Estas funciones que calculan una parte de la solución final reciben el nombre de procedimientos auxiliares.
Como regla, trata de formular definiciones o procedimientos auxiliares para todas las dependencias entre las cantidades que se mencionan en la definición del problema. En el ejemplo anterior, las relaciones obvias eran el área del círculo interior y el área del cuadrado. El nombre estándar de estos procedimientos auxiliares es subrutina y se presentó en el tema 2.
Por ejemplo, ¿cómo se le podría hacer para calcular el valor absoluto de un entero? En matemáticas se diría (y esto sirve como análisis del problema):
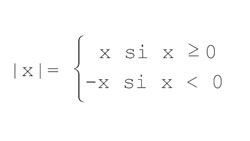
Por fortuna, Scheme incluye muchas primitivas para realizar este tipo de pruebas o comparaciones y también diversas formas de llevar a cabo una u otra alternativa. A continuación, algunas interacciones básicas:
> (= 5 5)
#t
> (> 5 6)
#f
> (> 5 3)
#t
> (>= 5 12)
#f
> (and (> 5 3) (> 5 2))
#t
> (or (> 5 7) (> 5 2))
#t
> (not (> 5 7))
#t
Los valores #t y #f son utilizados por Scheme para representar los valores de verdad, verdadero y falso respectivamente. Los procedimientos para hacer comparaciones numéricas, <, >, =, <= y >=, funcionan como lo esperado y los otros procedimientos son de lógica y representan la conjunción: and ("y" en español), la disyunción or ("o" en español), la negación not ("no" en español).
Aún no se puede construir el procedimiento para calcular el valor absoluto de un número. Falta un mecanismo para decidir entre distintas opciones. Hay varias alternativas en Scheme para realizar esta labor, las cuales se conocen como expresiones condicionales; la más general se da a través de la forma primitiva cond, cuya forma general es:

¡Ah!, por cierto, en Dr.Scheme se pueden utilizar paréntesis o corchetes de manera indistinta. En general, se utilizarán para facilitar la lectura cuando hay varios paréntesis juntos.
Regresando a las expresiones cond; el valor total de la expresión es la primera respuesta cuya pregunta sea verdadera. Considérense los siguientes ejemplos:
> (cond
[(> 5 6) 1]
[(< 5 6) 2]
[(= 5 6) 3]
)
2
> (cond
[(and (> 5 4) (= 5 6)) 1]
[(= 5 6) 2]
[else 3]
)
3
Obsérvese que tanto las preguntas como las respuestas son expresiones cualesquiera; sin embargo, en el caso de las preguntas, Scheme espera recibir un valor de verdad, ya sea falso o verdadero. Algo muy práctico es que en Scheme y en muchos otros lenguajes de programación, cualquier expresión que no es falsa (#f) es verdadera. Por ejemplo, 5 o (+ 3 5) son expresiones que se consideran verdaderas, aunque no correspondan a un valor de verdad, propiamente hablando. La expresión else funciona como último recurso y puede interpretarse como: "Si no hay otra opción, utilizar esta respuesta".
Ahora todo está listo para escribir un procedimiento que calcule el valor absoluto de un entero; ya se ha hecho el análisis y se puede proceder directamente a la receta de diseño:
;; Contrato: absoluto: n[entero] -> entero no-negativo
;; Propósito: calcular el valor absoluto de un entero
;; Ejemplo: (absoluto -3) debe producir 3
(define (absoluto n)
(cond [(>= n 0) n]
[(< n 0) (- n)]))
;; pruebas:
(absoluto 5)
(absoluto -5)
¿Qué nuevas cosas hay en este procedimiento absoluto? ¿Qué significa (- n)? Se supone que la operación – (resta) recibe dos argumentos, ¿o no? La respuesta es sí y no. La resta como se conoce es una operación binaria. Sin embargo, en Scheme, la mayoría de las operaciones matemáticas que son asociativas, como la resta, reciben desde uno hasta cualquier cantidad de argumentos. Analícense los siguientes ejemplos:
> (- 1)
-1
> (- 5 4 3)
-2
> (- 5 4 3 2 1)
-5
El último ejemplo sería equivalente a la operación:
> (- (- (- (- 5 4) 3) 2) 1)
-5
que es la versión que muestra la asociación para la resta de manera explícita. Es decir, la resta de cinco números se lee naturalmente de izquierda a derecha: a la resta de 5 menos 4, restarle 3; al resultado obtenido restarle 2 y al siguiente resultado restarle 1. Cuando la resta recibe un argumento único, como (- 5), funciona como la negación y por ello el resultado es -5.
La forma cond es muy general y resulta una práctica común en todos los lengua-jes de programación. Para los casos más típicos existen formas especiales; por ejemplo, cuando se quiere plantear una sola pregunta y decidir entre un camino u otro, izquierda o derecha, arriba o abajo, existe otra forma especial que se llama if. La sintaxis de if es más sencilla porque utiliza menos paréntesis:
(if pregunta respuesta-verdadera respuesta-falsa)
Es decir, la expresión respuesta-verdadera se evalúa cuando la pregunta regresa verdadero (#t); cuando regresa falso #f, se evalúa la expresión respuesta-falsa.
Reflexionando un poco sobre "la forma" de los procedimientos que se escribieron arriba, por ejemplo: absoluto. En este procedimiento se utilizó una expresión condicional con tres alternativas. ¿Qué sucede cuando se evalúa (absoluto -5)? Ocurren las siguientes acciones en orden consecutivo:
1] El intérprete nota que -5 es un número; entonces, evalúa el procedimiento absoluto y pasa como argumento -5.
2] El cuerpo del procedimiento es una expresión única condicional, así que se evalúa la primera pregunta: (> = n 0), donde n = -5; es decir, se evalúa por nuestro modelo de sustitución: (> = -5 0), que regresa falso, #f.
3] Finalmente se evalúa (< -5 0), que es verdadero, #t, y posteriormente la respuesta de esta alternativa: (- n); es decir (- -5), que regresa 5.
Es una ejecución lineal, pero recuérdese que los algoritmos realmente interesantes requieren repetir una tarea una y otra vez.
Curiosidades
La programación funcional es uno de los tipos fundamentales de programación o paradigma de programación, que trata los cómputos como evaluación de funciones matemáticas. Los lenguajes puramente funcionales evitan la mutación o modificación de datos. Scheme facilita el estilo funcional de programación, pero también soporta operaciones de mutación.