Anteriormente se mostraron varios ejemplos de algoritmos de distintas complejidades. Se vieron dos algoritmos para el problema de búsqueda ordenada: el secuencial (de tiempo lineal), y el binario (de tiempo logarítmico). Asimismo, se revisaron algunos algoritmos de tiempo cuadrático, como el exhaustivo empleado para encontrar la pareja de puntos más cercana. Y finalmente se habló en distintas ocasiones sobre algoritmos de tiempo exponencial. ¿Qué significan exactamente estos términos? ¿Por qué son tan importantes?
El algoritmo de búsqueda lineal simplemente recorre la lista de entrada de n elementos en busca de un elemento dado. Se dice que su tiempo de ejecución es lineal en el tamaño de la lista porque, en el peor caso, debe analizar n elementos. Esto implica que, independientemente de cuáles sean con exactitud las operaciones que ejecuta sobre cada elemento, conforme crece el tamaño de la lista de entrada n, el tiempo de ejecución del algoritmo se incrementa linealmente. Si en una ejecución con una lista de n elementos el tiempo es T, con una lista de 2n elementos, el algoritmo emplea 2T unidades de tiempo para terminar la ejecución en la máquina. Si se corre en una máquina cuatro veces más rápida, la búsqueda en una lista de n elementos tomará T/4. Sin embargo, al duplicar el tamaño de la lista, otra vez se duplica el tiempo de ejecución a T/2.
En resumen, aunque no es posible decir cuál es el tiempo de ejecución de un algoritmo para una entrada de cierto tamaño, ya que éste depende de una variedad de factores como la computadora elegida para correr el algoritmo y la programación del algoritmo en un cierto lenguaje, entre otros, sí se puede estimar cómo se incrementa el tiempo de ejecución conforme el tamaño de la entrada crece. Es posible definir formalmente esto como orden de crecimiento del tiempo de ejecución, o en general de cualquier función f(n).
En el caso de un algoritmo lineal, se afirma que su tiempo de ejecución es orden de n, y se escribe O(n). Esto significa que para el computólogo, 2n o 28n equivalen a lo mismo, ya que ambas funciones crecen a la misma velocidad. Es decir, se agrupan todas las funciones lineales en una sola clase, la llamada clase de funciones lineales, denotada O(n). Estas funciones no sólo incluyen cualquiera de la forma cn, para una constante c, sino también funciones como 4n + 7; esto es, de la forma cn + k, lo cual implica que tampoco afecta el orden de crecimiento sumar una constante; quizá sólo empezar a correr el programa de búsqueda lineal suma un cierto tiempo, k, el mismo para cualquier entrada posible, pero esta k no afecta el orden de crecimiento.
Además de indicar cómo se comportará el algoritmo cuando trabaje con problemas más grandes, también ofrece una buena indicación de qué tan eficientemente se aprovecha la tecnología de cómputo. Si el algoritmo lineal emplea 60 segundos en buscar en una lista de 100 elementos en una computadora que corre a cierta velocidad, supóngase que le toma x unidades de tiempo ejecutar cada instrucción. Si se hace una inversión para que resuelva el problema en la mitad de tiempo, 30 segundos, con una computadora del doble de velocidad, x/2 unidades de tiempo por instrucción, lograremos esto.
Por otro lado, un algoritmo de orden exponencial, O(2n), por ejemplo, es el de la búsqueda exhaustiva que realiza Arcadio descrita antes, y para encontrar todos los ordenamientos que vimos arriba, el orden es O = O(n!). En estos casos, duplicar la velocidad de la computadora no ayuda prácticamente en nada; sólo se podrá buscar en listas de unos cuantos elementos más. Por ejemplo, si el algoritmo es exponencial y un minuto alcanzaba para buscar en una lista de 1 000 elementos, con una computadora del doble de velocidad, quizá lograría buscar en una lista de 1 002 elementos.
Si el algoritmo de la búsqueda binaria, cuyo tiempo de ejecución es O(log n), empleara, por ejemplo, 10 segundos en buscar en una lista de 1 000 elementos, para duplicar su tiempo de ejecución se tendría que llegar a una lista de hasta un millón de elementos. Este tipo de comportamiento establece una diferencia radical entre un algoritmo de tiempo lineal y uno logarítmico, independientemente de la computadora en la que se corran. De hecho, la diferencia es tan radical como cuando se pasa de un algoritmo polinomial a uno exponencial. Además, nótese que ya no hace falta especificar la base del logaritmo, ya que la diferencia entre una base y otra es sólo una constante.
La notación asintótica es aquella que expresa el orden de crecimiento de una función, sin tomar en cuenta cómo se comporta al inicio ni las constantes multiplicativas. Un ejemplo es la "O grande" descrita arriba. Es útil para simplificar las funciones analizadas, ignorando detalles como términos de crecimiento más rápido. Es decir, en la práctica, la notación permite afirmar que la función que analizamos crece como otra función más sencilla.

Richard Karp
(1935) ganó el Premio Turing en 1985 por sus contribuciones a la teoría de algoritmos, y por identificar al crecimiento polinomial como lo deseable de un algoritmo práctico, además de desarrollar la metodología para probar que un problema es NPcompleto.
Por ejemplo, se vio un algoritmo de ordenamiento con tiempo de ejecución (n − 1)n/2 = (n2 − n)/2, lo cual es simplemente O(n2), ya que la función anterior no crece más rápido que n2. Se presentó un algoritmo para las torres de Hanoi, cuyo número de movimientos era 2n − 1.
Otros ejemplos de crecimiento exponencial pueden tener funciones de crecimiento del estilo: 2n + 2n, 2n + 356 y 2n + 3n3 + 2n; empero, todas ellas tienen O(n) = 2n, porque si la n es lo suficientemente grande, la aportación de los demás términos no afecta la velocidad de crecimiento. Sin embargo, es importante mencionar que 3n crece estrictamente más rápido que 2n. Esto es, aunque a cualquier función de la forma cn se le llame exponencial, no todas tienen el mismo orden de crecimiento. Y lo mismo para n!, que crece más rápido que cualquier función exponencial.
De la misma manera, las funciones de crecimiento polinomial, O(nc), incluyen, por ejemplo, a n2 y a n7, aunque tienen distinto orden de crecimiento. En efecto, n crece me nos rápido que n2, y ésta menos rápido que n3. No obstante, n log n crece menos rápido que n2, y aquí radica la complejidad de los mejores algoritmos para ordenar una lista. ¿Cuál sería el orden de crecimiento del tiempo de un algoritmo que no crece? Por ejemplo, para decidir si un número es par o impar, basta con examinar su dígito menos significativo, independientemente del tamaño del número. Es decir, el tiempo crece a la misma velocidad que una función constante (que no crece), como f(n) = 23, o simplemente f(n) = 1. Es decir, estas funciones son O(1).
Entonces, ¿cuál es el orden de crecimiento más rápido? Pues, no existe tal. Para cualquier orden de crecimiento, por ejemplo f(n), siempre hay uno aún más rápido. Por ejemplo 2f(n). Todavía más sorprendente es que existen problemas tan difíciles que requieren de ese tiempo de ejecución.
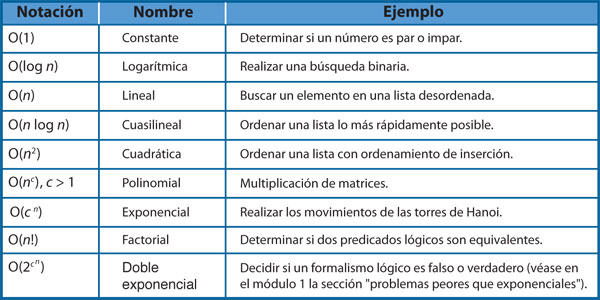
En la tabla anterior se listan algunos de los órdenes de crecimiento que aparecen con frecuencia en el análisis de algoritmos, así como ejemplos de algoritmos cuyas funciones presentan ese orden de crecimiento.