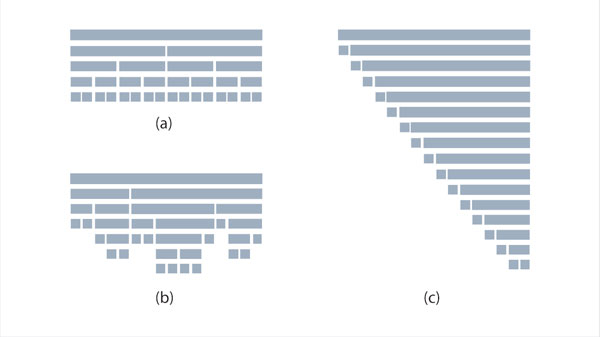
Es probable que el algoritmo de ordenamiento más utilizado en la práctica sea el de ordenamiento rápido (quicksort, en inglés), que tiene complejidad, en el peor de los casos, proporcional a n2; sin embargo, la complejidad del caso promedio es de n log n. Los pasos de este algoritmo son:
1] Seleccionar un elemento de la lista, al que se llamará "pivote".
2] Reordenar la lista para que todos los números menores que el pivote queden del lado izquierdo y los mayores del derecho. El pivote se encuentra en su posición final, que se denomina "la partición".
3] Ordenar la lista de elementos menores y la de elementos mayores, de manera recursiva.
El ordenamiento rápido es un ejemplo de algoritmo no determinista, ya que deja libertad en cuanto a la elección del pivote. En el mejor caso, en cada iteración la lista se divide a la mitad y la recursión se repite log n veces. Como en cada nivel hay que trabajar con n elementos para dividirlos de acuerdo con el pivote, el tiempo total es n log n. Pero con mala suerte, el pivote podría ser el menor de la lista, y en cada llamada recursiva dividirla en dos partes, una con un solo elemento y otra con todos, en cuyo caso el tiempo de ejecución sería proporcional a n2.