Aquí presentamos un algoritmo de "divide y vencerás" sencillo, pero muy útil. De hecho, en este caso no hace falta el procedimiento de combinar las soluciones con los dos subproblemas, ya que sólo una de ellas aparece.
Si un directorio telefónico, como el de la Ciudad de México, que puede tener cientos de miles de números telefónicos, no estuviera ordenado alfabéticamente, no se tendría otra opción que buscar el número de una persona, nombre por nombre. Si tuviera 100 000 nombres, y tomara un segundo revisar cada uno, un usuario tardaría casi 30 horas en revisar todos los nombres. Afortunadamente, el directorio sí esta ordenado, y para buscar un nombre sólo se tiene que, por ejemplo, abrir el directorio a la mitad, y esa mitad dividirla en otra, guiándose por el orden alfabético de nombres.
¿Cuánto tiempo le toma a una persona buscar el nombre de otra en el directorio? Tantas veces como se tenga que dividir 100 000 entre 2 una y otra vez, hasta llegar a un número muy pequeño. A esta operación se le conoce como logaritmo en base 2 de 100 000. En este caso, es suficiente hacer 17 comparaciones, en lugar de emplear 30 horas con 15 segundos.
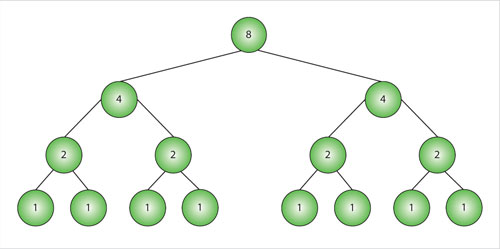
El algoritmo de búsqueda exhaustiva recorre la lista de principio a fin, y su tiempo de ejecución es proporcional al tamaño de la lista, n. El paradigma "divide y vencerás" conduce al algoritmo de búsqueda binaria descrito arriba. El tiempo de ejecución de éste es proporcional al logaritmo en base 2 de n; como lo muestra la siguiente gráfica, llamada árbol binario, es igual al número de veces que hay que dividir n entre 2 para llegar a 1.
El problema de búsqueda ordenada tiene como entrada una lista de n números, ordenados de menor a mayor, y un número x. La salida es la posición de x en la lista, o es un "no", en caso de que x no se encuentre en la lista.
En la figura se presenta el caso de una lista de ocho números, donde se observa que el logaritmo en base 2 de 8 es igual a 3, representado por el número de aristas que hay que recorrer para llegar de la raíz, el vértice etiquetado con 8, hasta una hoja, con valor 1.