En muchas ocasiones es posible evitar la búsqueda exhaustiva y diseñar algoritmos más eficientes para resolver un problema, sin necesidad de considerar todas las posibles soluciones explícitamente. Una manera de lograrlo es mediante el método "divide y vencerás", que construye una solución poco a poco, cada vez más completa. El paradigma "divide y vencerás" es la clave para diseñar algoritmos muy eficientes para una variedad de problemas. La idea es dividir un problema en dos subproblemas del mismo tipo y tamaño; resolverlos de manera recursiva y combinar las soluciones para obtener el resultado deseado. Para que el paradigma resulte en un algoritmo eficiente es necesario que el procedimiento de combinar las soluciones con los subproblemas sea veloz. Aunque es habitual describir este tipo de algoritmos recursivamente, también se puede hacer de forma iterativa.
Para el caso del problema de ordenamiento, son sorprendentes los números tan grandes que se obtuvieron con una tarea aparentemente tan sencilla como ordenar una lista. Las amas de casa ordenan sus listas de compras cuando van al supermercado para que les sea más fácil encontrar los objetos; los carteros ordenan la correspondencia diaria para entregar cientos de cartas y paquetes; las bibliotecas mantienen ordenados sus libros; los profesores ordenan las listas de calificaciones de alumnos por sus apellidos; sería casi imposible encontrar un número telefónico en el directorio si los nombres no estuvieran ordenados.
Si se tiene una lista con n números enteros y se desea ordenarla crecientemente (de menor a mayor), no se hace una búsqueda sobre el conjunto de todos los posibles ordenamientos; es posible hacerlo de muchas otras maneras más eficientes. Cuando juegas cartas con tus amigos o tu familia, ¿cómo se podría ordenar un juego? Bueno, pues hay distintas maneras de hacerlo.
Supóngase que alguien reparte las cartas, una por una. Cada vez que te da una carta, la insertas en el lugar correcto entre las que ya tienes en la mano. Este algoritmo se conoce como ordenamiento por inserción y, aunque en general no es el más rápido de los ordenamientos, se puede utilizar el mismo algoritmo para ordenar un paquete de cartas de cualquier tamaño, incluso si no te dan una por una.
En términos abstractos, al trabajar con una lista de números en lugar de cartas, cada iteración del ordenamiento por inserción quita un elemento de la parte desordenada de la lista, el i-ésimo elemento, y lo inserta en la posición correcta en la parte ordenada de la lista. Repetir esto, con el i + 1-ésimo elemento, y así sucesivamente, hasta que no haya más elementos en la parte desordenada de la lista.
Ordenamiento por inserción
Entrada: lista L de n números
Salida: lista ordenada
Para i desde 1 hasta n, ejecutar:
Tomar el i-ésimo elemento de L, por ejemplo x
Insertar x en su lugar correcto dentro de las primeras i posiciones de L.
Queda definir el algoritmo para insertar un elemento en una lista ordenada. Es decir, se ha diseñado el algoritmo usando la noción de subrutina y siguiendo una estrategia muy útil llamada de "arriba abajo" (que consiste en ir resolviendo un problema poco a poco, primero las dificultades generales, dejando algunas tareas más particulares para ser resueltas posteriormente). De esta manera, se resuelve el problema paulatinamente y damos libertad a la implementación de la subrutina. Al algoritmo de ordenamiento no le interesa de qué manera inserta el elemento. Con tal de que lo haga correctamente, puede buscar su posición de derecha a izquierda en la lista ordenada, esto es, de mayor a menor, o viceversa. Lo usual es que lo haga de derecha a izquierda.
Concepto
A la porción de un algoritmo que realiza una tarea específica y es relativamente independiente del resto del algoritmo, se le denomina subrutina o, dependiendo del lenguaje de programación y otras sutilezas, procedimiento, función o método. El uso de subrutinas dentro de un algoritmo o programa tiene muchas ventajas, como:
• reducir la duplicación de secciones que hacen la misma tarea;
• reutilizar las subrutinas en otros algoritmos;
• descomponer algoritmos complejos en partes más simples, y
• facilitar la comprensión y análisis del algoritmo
Para determinar que el algoritmo de ordenamiento es correcto, el primer paso será analizarlo por inducción, suponiendo que la subrutina de inserción funciona correctamente. Se presume que después de i iteraciones, ha ordenado de manera correcta los primeros i elementos de la lista, y se observa que después de una iteración, ordena correctamente los primeros i + 1 elementos. Ahora, se puede analizar de manera similar la subrutina y por inducción probar que funciona. ¿Cuál sería la hipótesis de inducción en cada caso?
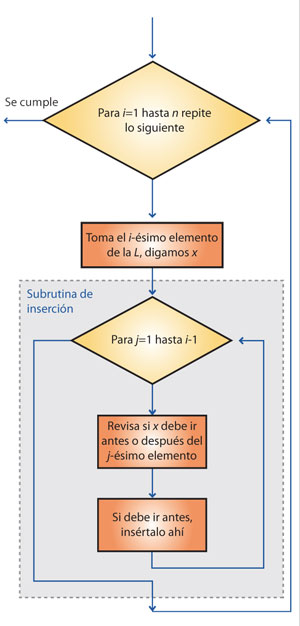
Para analizar el tiempo de ejecución del algoritmo es útil ver su diagrama de flujo, que incluye dos iteraciones anidadas: se repite la exterior n veces y, por cada una, la interna se repite varias veces, lo cual usualmente da lugar a algoritmos de tiempo cuadrático.
Obsérvese que ejecuta n iteraciones, y que en la primera debe insertar el primer elemento en la parte ordenada de L, que al inicio está vacía. En la segunda iteración debe insertar el segundo elemento en la parte ordenada de L, que ahora tiene un elemento. En general, en la i-ésima iteración debe insertar el i-ésimo elemento de L, por ejemplo x, en la parte ordenada de L, que ahora consiste de los primeros i − 1 elementos. Para hacerlo, debe revisarlos y comparar cada uno de ellos con x. Es decir, en la i-ésima iteración se pudieron haber realizado i − 1 comparaciones. Llega al último elemento, el n-ésimo, que inserta en una lista de n − 1 elementos, para obtener un total de:
1 + 2 + 3 + …+ n – 1
comparaciones, en el peor caso (sobre todas las posibles listas de entrada). Y ya se vio que esta suma es igual a n(n − 1)/2. Por ejemplo, si la lista original tiene dos elementos, con una comparación basta para saber si se dejan así o se invierten.
Concepto
Como se deduce de las actividades anteriores, el algoritmo de ordenamiento por inserción tiene un tiempo de ejecución que crece de manera cuadrática con respecto al tamaño de su entrada, n, en el peor caso (como cuando el orden de la lista está totalmente invertido). Sin embargo, para ciertas entradas (cuando la lista está ordenada), su tiempo de ejecución es lineal. En general, al analizar un algoritmo se considera su tiempo de ejecución en el peor caso, ya que éste muestra el tiempo máximo que emplea el algoritmo en resolver el problema tomando en cuenta todas sus entradas posibles (en algunas le tomará más tiempo y en otras menos).
El algoritmo de ordenamiento por inserción es mucho mejor que buscar entre todos los n! ordenamientos posibles. Sin embargo, existen algoritmos aún mejores, como se podrá ver más adelante. No obstante, este algoritmo funciona bien para listas pequeñas; conforme crece la lista, el tiempo de ejecución se incrementa rápidamente, y es necesario utilizar algoritmos más eficientes.
La característica de estabilidad de un algoritmo de ordenamiento permite ordenar, por ejemplo, una lista de alumnos con sus calificaciones: primero por calificación y luego por orden alfabético. Generalmente, permite ordenar listas de elementos con más de un criterio.
Concepto
Cuando el tiempo empleado para resolver un problema depende de alguna potencia del tamaño de la entrada, como n2 o n3, se dice que el problema es de complejidad polinomial. Al conjunto de todos los problemas de complejidad polinomial los computólogos lo bautizaron como P.