La búsqueda exhaustiva no siempre genera algoritmos exponenciales. A continuación se presentará un ejemplo básico de geometría computacional, un área con diversas aplicaciones de computación, especialmente relacionadas con imágenes y visión.
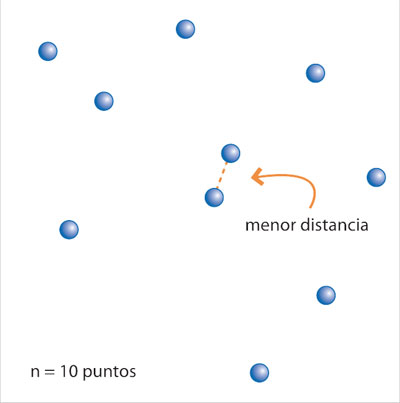
En el problema de los puntos más cercanos, la entrada es un conjunto de n puntos en el plano, y la salida es la menor distancia entre algún par de puntos.
El método de fuerza bruta para resolver el problema es simplemente considerar uno por uno todas las parejas de puntos; para cada pareja hay que calcular a qué distancia se encuentran, y elegir la menor de las distancias.
Algoritmo PC-exhaustivo
Para cada pareja de puntos x, y:
Sea d la distancia de x a y
Si d es menor a d min, la menor distancia vista hasta ahora,
Sea d min igual a d.
Para ejecutar este algoritmo, se supone que la máquina sabe calcular la distancia entre dos puntos, comparar dos de estas distancias para obtener la menor y entregar una por una todas las posibles parejas de puntos. En realidad, estas operaciones se pueden implementar fácilmente en cualquier lenguaje de programación.
Se ha visto en el tema de inducción que hay n(n − 1) parejas y que el tiempo de ejecución de este algoritmo crece de manera cuadrática conforme se incrementa el tamaño de la entrada. Es decir, mientras que en un algoritmo lineal, como el de coloración de mapas con seis colores, si el número de países del mapa se duplica, el tiempo para resolver el problema también se duplica; en el caso del algoritmo de los puntos más cercanos, el tiempo se cuadruplica. Esto se explicará con mayor detalle en el siguiente tema. Existe otro algoritmo mucho más eficiente que éste.