Ahora se verá otro ejemplo con más detalle, en el que es necesario pedir ayuda dos veces en lugar de una, para resolver problemas más pequeños.
Regresando al problema de las torres de Hanoi del capítulo 1, se tienen tres torres: A, B y C. Al principio, en una de las torres, por lo general la torre A, se encuentran apilados n anillos, digamos n = 3 anillos, de distintos diámetros, colocados de mayor a menor en forma ascendente. El objetivo del problema es, dando como entrada el número n, producir como salida los movimientos necesarios para mover todos los anillos a otra torre, uno por uno. Cada movimiento debe efectuarse de la siguiente forma: tomar el anillo que se encuentra hasta arriba de la torre X y colocarlo hasta arriba de la torre Y, donde X y Y pueden tomar cualquiera de los valores A, B o C. Este movimiento puede ejecutarse siempre y cuando el anillo que se coloque en la torre Y no descanse sobre un anillo de menor diámetro.
Antes de diseñar un algoritmo que resuelva el problema, es conveniente colocar las torres en círculo; si se colocaran en línea se establecería una diferencia entre las torres: una sería la primera y otra la última. En cambio, en un círculo todas son iguales y se pueden recorrer en el orden de las manecillas del reloj, por ejemplo.
Obsérvese que un algoritmo es una descripción detallada y precisa de cómo resolver un problema, que consiste en una secuencia finita de instrucciones. Esta secuencia recibe algunos datos como entrada, los procesa a través de las instrucciones y produce datos como salida. Asimismo, las instrucciones de un algoritmo están diseñadas para ejecutarse a través de una máquina que entiende lo que significa cada instrucción, y sabe cómo ejecutarla.
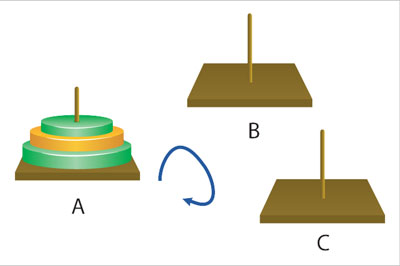
En el caso de las torres de Hanoi, las instrucciones indican que se debe tomar el anillo situado hasta arriba de la torre X y colocarlo hasta arriba de la torre Y, donde X y Y pueden adoptar cualquiera de los valores A, B o C.
El diseño del algoritmo utiliza una idea sencilla. Al principio no hay otra opción que mover el anillo más pequeño, por ejemplo, a la torre B. Una vez que se mueve, si n = 1, se ha resuelto el problema. Si n > 1, como no tiene caso desplazar ese anillo otra vez, sólo queda un anillo que se puede mover, es decir, el que le sigue en tamaño, y sólo hay una torre en donde es posible ubicarlo, la torre C.

Si se piensa un poco, se observa que al que se debe mover ahora es al menor, y que conviene moverlo a la torre C, ya que si se mueve a la torre A, se terminaría en una configuración equivalente, pero habríamos ejecutado tres movimientos en lugar de uno.
Eventualmente es necesario trasladar el anillo más pequeño y debe hacerse en sentido circular, de la torre A a la B y posteriormente a la C, para luego regresar a la A, y así sucesivamente. Una vez que se ha movido, no tiene caso desplazarlo de nuevo, por lo que no hay otra opción que utilizar otro anillo; de hecho, sólo hay un anillo que se puede mover o ninguno si ya se terminó de mover todos los anillos. El algoritmo es el siguiente:
1] Repetir lo siguiente hasta que el paso (1.b) no se pueda ejecutar:
(1.a) Mover el anillo más pequeño a la torre siguiente en el orden de las manecillas del reloj.
(1.b) Ejecutar el único movimiento permitido posible que no involucre al anillo más pequeño.
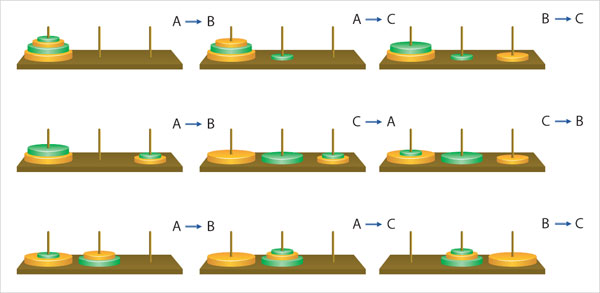
En la siguiente figura se muestra la ejecución de las ocho primeras instrucciones del algoritmo, con las torres A, B y C ordenadas en círculo.
Concepto
Un algoritmo resuelve un problema computacional, pero no necesariamente acerca de computadoras.
Como se vio anteriormente, para hablar de un algoritmo se requiere saber a qué máquina se dirige y qué instrucciones sabe ejecutar. Las instrucciones deben ser lo suficientemente precisas para que al utilizarlas en el diseño del algoritmo, se aprenda algo acerca del problema. Un algoritmo que diga: "Ve con un chamán y dile que adivine la secuencia de movimientos", no dirá mucho acerca de las torres de Hanoi.
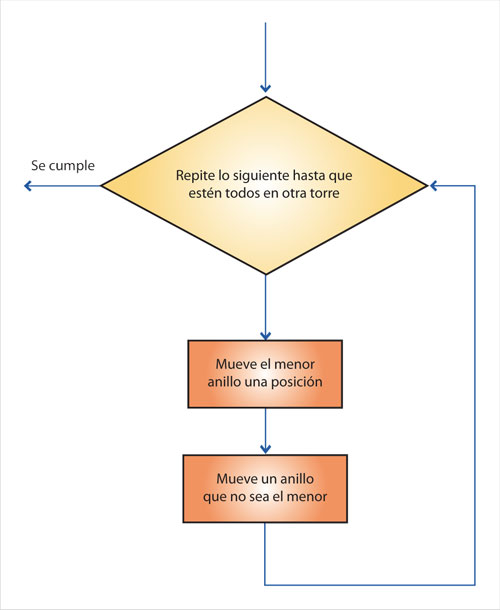
Lo primero que se deja entrever es que el algoritmo consiste en una lista finita de instrucciones, y sin embargo puede resolver cualquier cantidad de entradas al problema; es decir, no importa con cuántos anillos n comencemos, ni en qué torre estén acomodados, el algoritmo resuelve el problema. Es claro, entonces, que cualquier algoritmo requerirá de algún tipo de instrucción que implique ejecutar repetidamente un bloque de instrucciones. Es posible visualizar al algoritmo anterior mediante un diagrama de flujo.
Nótese que no todos los algoritmos requieren instrucciones de repetición. Si el problema es muy simple, podría no hacer falta este tipo de instrucciones. Por ejemplo, si el problema pide tomar el anillo más pequeño, un algoritmo útil sería simplemente identificar en cuál de las tres torres están colocados los anillos y tomar el anillo situado en la parte superior de la pila.
Ahora bien, incluso sin tener que analizar con detalle las instrucciones del algoritmo y sin necesidad de que el problema lo diga explícitamente, debe notarse que no está enfocado para resolver un problema de robótica o ingeniería mecánica. No se piensa en el hecho de que para resolver un problema de esta índole es necesario diseñar un dispositivo que pueda localizar, mediante la visión, dónde está un anillo y construir un brazo mecánico que lo sujete y mueva otra torre. Más bien, el interés se encuentra en qué secuencia de movimientos de discos es la que resolvería el problema. Ni siquiera se trata de un problema físico, no es necesario tener a la mano un juego de madera con tres varillas y anillos; es factible pensar en soluciones, dibujarlas en papel, inclusive mediante símbolos que indiquen cuántos anillos tiene cada torre. Por supuesto, aunque se pueden imaginar las soluciones y los movimientos de los anillos, tampoco se trata de un problema de psicología. Es un problema de computación, a pesar de que se propone una solución y se analiza su eficiencia y corrección, sin necesidad de una computadora.
En efecto, la entrada al algoritmo en realidad no son los anillos ni las varillas de madera. La entrada es sencillamente el número n. Lo sorprendente es que la n no aparece en el algoritmo y sin embargo funciona para cualquier valor de n. Como siempre, la entrada debe ser válida; no sirve de nada un número como 3.45. En este caso, cualquier número entero mayor o igual a cero es una entrada válida. La salida es una lista de movimientos que, al ejecutarlos, permiten que los discos se desplacen a otra torre sin que se haya realizado un movimiento prohibido.
Un problema siempre supone un cierto nivel de detalle. En el caso del algoritmo de las torres de Hanoi, se supone, entre otras cosas, que se puede localizar la torre con el anillo más pequeño.
¿Pero cuáles son las instrucciones de este algoritmo? Se había mencionado que las instrucciones son: tomar el anillo ubicado en la parte superior de la torre X y colocarlo en la parte superior de la torre Y. Como hay un solo anillo hasta arriba de una torre y siempre se coloca hasta arriba de otra, es suficiente señalar de qué torre a qué torre se ejecuta el movimiento. Es decir, se puede simplemente usar instrucciones de la forma:
X = > Y
Entonces, la salida del algoritmo debe ser una lista de este tipo de intrucciones. Por ejemplo, para n = 2 discos, una salida válida sería:
A = > B, A = > C, B = > C
para que los dos discos queden acomodados en la torre C.
Se podría pensar que éste es el único tipo de instrucción requerido, además de las instrucciones de repetición mencionadas. Sin embargo, al analizar las instrucciones del algoritmo, se puede ver que son más complicadas:
• Instrucciones de repetición. Este algoritmo tiene una sola instrucción de este tipo, la 1: "Repite lo siguiente, hasta que el paso 1.b no se pueda ejecutar". Esta instrucción, como cualquier otra instrucción de repetición, tiene tres componentes: primero, su nombre, el que nos indica qué se pretende hacer, en este caso, "repite"; en segundo lugar, una manera de indicar cuál es el bloque de instrucciones que se deben repetir, que en este caso se trata simplemente de las dos instrucciones que siguen, la 1.a y la 1.b; finalmente, es necesario indicar cuántas veces se debe repetir el bloque de instrucciones. Se solicita repetirlo hasta que se cumpla determinada condición; el ejemplo indica repetir "hasta que el paso b no se pueda ejecutar", es decir, hasta que todos los anillos se encuentren en una sola torre.
• La siguiente instrucción, la 1.a, es: "Mueve el anillo más pequeño a la torre siguiente en el orden de las manecillas del reloj". Se supone que quien ejecuta esta acción puede localizar la torre con el anillo más pequeño, además de mover un anillo de una torre a otra.
• La última instrucción, la 1.b, indica: "Ejecuta el único movimiento permitido posible que no involucre al anillo más pequeño". Es de suponer que el ejecutor de la acción puede buscar una torre con el anillo que le sigue al más pequeño en tamaño, o bien, decir si no hay tal, debido a que todos se encuentran en una sola torre. De este modo se señala que las repeticiones solicitadas por la primera instrucción han concluido.
El modelo de cómputo describe la máquina a la cual se hace referencia, el dispositivo, físico o imaginario, que sabe cómo ejecutar un conjunto de instrucciones dado. La algorítmica estudia los métodos para resolver problemas en un determinado modelo de cómputo, con especial interés en que las soluciones sean eficientes.
Para analizar la eficiencia de un algoritmo es necesario saber algo más acerca del modelo de cómputo; por ejemplo, los costos que conlleva ejecutar un algoritmo en el modelo. Se pueden evaluar muchos costos, pero el más importante es, por lo general, el tiempo que lleva ejecutar el algoritmo. Como no se conoce de antemano el dispositivo físico que lo ejecutará (o incluso si se pretende que algún dispositivo lo ejecute), lo que se hace con frecuencia es suponer que cada instrucción emplea una unidad de tiempo para ser ejecutada, sin necesidad de especificar el tipo de unidad (un segundo, un minuto o alguna otra).
Por lo tanto, el tiempo utilizado para ejecutar un algoritmo equivale al número de instrucciones para resolver el problema. En el caso de las torres de Hanoi, simplemente se cuentan las instrucciones 1.a o 1.b, sin entrar en más detalles que no se conocen de antemano, como en cuántos segundos se ejecuta una instrucción en una computadora. Es de esperar que, mientras más grande sea la entrada al algoritmo, mayor será el número de instrucciones por ejecutar.
Respecto al algoritmo de las torres de Hanoi, se verá más adelante cómo demostrar 2n − 1. Por el momento, se comprobará con algunos ejemplos:
• n = 1, la fórmula da exactamente 21 − 1 = 2−1 = 1. Es decir que en un solo movimiento se traslada el único anillo de una torre a la siguiente en el sentido de las manecillas del reloj, ejecutando la instrucción 1.a. Nótese que esto es precisamente lo que se logra después de ejecutar un movimiento, A => B, en la figura anterior.
• Otro caso que se ilustra en la figura es el de n = 3, donde 23 − 1 = 8 − 1 = 7. Obsérvese que después de siete movimientos se ha logrado mover tres anillos de la torre A a la B.
Posteriormente se verá cómo demostrar esta fórmula en general. De hecho, es posible demostrar que el algoritmo es óptimo en cuanto a su tiempo de ejecución. No hay manera de mover n anillos de una torre a otra usando menos de 2n − 1 movimientos.
Concepto
Se puede evaluar qué tan bueno o eficiente es un algoritmo desde muchas perspectivas. Por ejemplo, cuánto tiempo emplea para resolver una tarea, cuánta memoria requiere, qué tan largo y difícil de entender es, etcétera.
Concepto
La complejidad de tiempo del algoritmo se define como el número de instrucciones a ejecutar, como función del tamaño de la entrada.
Curiosidades
Los errores de software pueden ocasionar enormes pérdidas de dinero e incluso de vidas humanas. Por ejemplo, un error en uno de los algoritmos de división del procesador Intel Pentium ocasionó pérdidas a la compañía por más de 400 000 000 de dólares, pues tuvo que reemplazar el producto a sus clientes.
Una vez diseñado un algoritmo se desea saber qué tan bueno es y, sobre todo, asegurarnos de que resuelve el problema correctamente.
Es correcto el algoritmo? El algoritmo de las torres de Hanoi es un ejemplo de lo difícil que puede resultar entender por qué resuelve el problema. Incluso tratándose de un algoritmo aparentemente tan simple como éste. La clave para entender por qué el algoritmo funciona correctamente radica en percatarse de que resuelve el mismo problema en casos más pequeños (valores de n menores), una y otra vez.
• Cada vez que se mueve un anillo por primera vez, se hace porque hay una torre vacía. Este anillo obviamente se encuentra en la torre A. Si no hubiera una torre vacía, en las otras dos torres habría anillos más pequeños y el algoritmo indicaría mover alguno de ellos, en lugar de éste: el menor, de acuerdo con la instrucción 1.a, o el otro de acuerdo con la 1.b.
• Cuando se tiene una torre vacía como la del inciso anterior, se pueden presentar tres posibilidades: estar al inicio o al final del algoritmo con dos torres vacías; o bien, con sólo una torre vacía. En este caso, en la torre A se encuentran los anillos que nunca se han movido y en otra torre el resto, por ejemplo m anillos, que están apilados necesariamente en orden de mayor a menor. Es decir, el algoritmo resuelve el problema de las torres de Hanoi para m anillos.
Considérese la penúltima situación en la figura anterior, donde se tiene el anillo más grande en la torre A, que nunca se ha movido y los tres restantes en la torre B. Esto es, se ha logrado resolver el problema para tres anillos. El algoritmo indica ejecutar la instrucción 1.b y mover el único anillo más grande a la torre C para llegar a la última configuración de la figura. Nótese que este momento equivale a comenzar el algoritmo desde el principio, sin este anillo mayor, puesto que nunca se moverá. Es decir, el algoritmo moverá los tres anillos de la torre B a la C, como si el anillo mayor no existiera. Se procederá a revisar esto con más detalle a continuación.
Muchas veces no se comprende bien una situación difícil o un problema agobiante, porque no se le observa desde la perspectiva adecuada. Para comprender mejor el algoritmo de las torres de Hanoi conviene seguir una línea de razonamiento y expresar de manera explícita cómo se resuelven problemas grandes, basados en la solución de problemas pequeños.
Supóngase que Arcadio recibe, como regalo de Úrsula, un juego de torres de Hanoi con cuatro anillos. Arcadio decide que para resolver este acertijo lo mejor es pedir la ayuda de su amigo Luis, gran aficionado a los acertijos, a quien le pide que resuelva un acertijo con sólo tres anillos, y que utilice las soluciones resultantes para resolver el acertijo con los cuatro anillos.
Arcadio muestra a Luis sus torres de Hanoi, pero con sólo los tres anillos más pequeños, y esconde el anillo más grande. Después de explicarle las reglas de los movimientos de los anillos, lo reta a que resuelva el problema de moverlos de una torre a otra. Le explica:
Pongo los anillos en una torre, digamos la torre X, y te indico a qué torre los debes mover; por ejemplo, a la torre Y. Tienes que anotar en un papel la lista de movimientos que hay que hacer.
Arcadio le dice a Luis que es suficiente con que la lista de movimientos indique de qué torre a qué torre se realiza cada movimiento; es decir, cada elemento de la lista es de la forma X => Y. Para evitar confusiones o trampas, Arcadio decide mostrar un papel a Luis donde indica el problema a resolver:
Resuelve TH (3, Fuente, Libre, Destino)
Fuente, Libre y Destino toman alguno de los valores A, B, C. Al recibir el papel, Luis entiende que tiene que regresarlo a Arcadio con la serie de movimientos que hace falta hacer para mover tres anillos de la torre Fuente a la torre Destino auxiliándose de la torre Libre.
Por ejemplo, Arcadio escribe:
Resuelve TH (3, C, A, B)
y Luis le regresa el papel con la siguiente anotación:
C = > B, C = > A, B = > A, C = > B, A = > C, A = > B, C = > B
Arcadio entrega a Luis varios papeles con cambios en la torre de inicio y de destino, y comprueba con satisfacción que Luis siempre responde con rapidez y precisión.
Arcadio resuelve fácilmente el acertijo para cuatro torres. Si desea moverlas de la torre A a la C, simplemente le pide a Luis:
Resuelve TH (3, A, C, B)
ejecuta los movimientos con los tres anillos menores y ejecuta:
A = > C
Luego pide a Luis:
Resuelve TH (3, B, A, C)
No hay como pedir ayuda para resolver un problema. Y Arcadio, muy feliz, se percata de que, al saber cómo resolver el acertijo para tres anillos, lo puede aplicar para cuatro, moviendo los anillos de una torre a cualquier otra y contestando cualquier pregunta de la forma:
Resuelve TH (4, X, Y, Z)
con los movimientos indicados:
Resuelve TH (3, X, Z, Y)
X = > Z
Resuelve TH (3, Y, X, Z)
Ahora, Arcadio claramente puede resolver el problema para cinco anillos sin ayuda de nadie más, ya que conoce el procedimiento para resolver los acertijos de cuatro anillos. En particular:
Resuelve TH (5, X, Y, Z)
para lo cual necesita ejecutar los movimientos indicados:
Resuelve TH (4, X, Z, Y)
X = > Z
Resuelve TH (4, Y, X, Z)
Arcadio se percata de que no era necesario llamar a una eminencia en descifrar acertijos como Luis; hubiera sido suficiente pedirle a su hermanito de dos años que resolviera:
Resuelve TH (1, X, Y, Z)
es decir, que moviera un solo anillo de la torre X a la Z. Al utilizar la solución para este acertijo, resuelve el problema para dos anillos. Más aún, Arcadio podría recurrir a la ayuda de su sobrino de un año de edad. ¿Qué debe contestar el pequeño cuando le pida que resuelva lo siguiente?
Resuelve TH (0, X, Y, Z)
¡Nada! Claro, la lista de movimientos necesarios para resolver el acertijo con cero discos es una lista vacía, sin ningún movimiento.
En general, para cualquier número de anillos n se tiene el siguiente algoritmo recursivo:
Resuelve TH (N, Fuente, Libre, Destino)
Si N es 0…
Ningún movimiento
De otro modo,
Resuelve (N - 1, Fuente, Destino, Libre)
Mueve Fuente = > Destino
Resuelve (N - 1, Libre, Fuente, Destino)
cuya operación se representa en la siguiente figura adjunta.
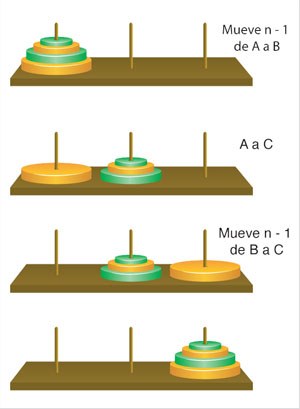
Si se usa una simple inducción, se puede demostrar que el algoritmo recursivo de las torres de Hanoi es correcto. Primero se prueba el caso base de n = 0 anillos, donde, obviamente, se puede resolver sin ejecutar ningún movimiento. O el caso de n = 1 anillo, donde el algoritmo indica:
• Resolver el caso de 0 anillos y como resultado no hacer movimientos.
• Mover el anillo de la fuente al destino.
• Resolver el caso de 0 anillos y como resultado no hacer movimientos.
Posteriormente, se demuestra el caso general. Supóngase que el amigo al que se le pide que devuelva la lista de instrucciones para resolver los casos de n − 1 anillos lo hace siempre correctamente. Es claro, entonces, que si se utilizan las soluciones de casos menores, se resolverá el problema como lo muestra la figura anterior.
Concepto
Un algoritmo recursivo se define en términos de sí mismo. Dice algo así como: "para resolver el problema de tamaño n utiliza soluciones al problema de menor tamaño". De manera similar, una definición recursiva es aquella que está dada en términos de sí misma. Dice cómo obtener conceptos nuevos, usando el mismo concepto que desea describir. Al igual que con los algoritmos, para que no sea una definición circular, es necesario que esté planteada en términos de una versión más pequeña de ella misma.
La forma recursiva del algoritmo facilita el análisis de su complejidad. Denotando como Mov(n) al número de movimientos que ejecuta el algoritmo, se ha visto que
Mov(0) = 0
y en general, el algoritmo recursivo indica que para resolver el caso de n anillos se resuelve el de n – 1 dos veces y se ejecuta un movimiento entre ambas soluciones:
Mov(n) = 2 × Mov(n − 1) +1
Si se emplea la inducción podemos verificar fácilmente que
Mov(n) = 2n – 1
¿Es esto lo mejor posible? Al inicio de este capítulo se mencionó que uno de los aspectos de la algorítmica tiene que ver con la búsqueda del mejor algoritmo posible para resolver un problema. Esta tarea es difícil, ya que para estar seguros de que un algoritmo es el mejor, de alguna manera hay que demostrar que no existe ningún algoritmo que lo supere. ¿Se puede estar seguro de que es imposible que alguien, en un futuro lejano, mediante un método ingenioso y conocimientos avanzados, diseñe un mejor algoritmo? En pocas palabras, hay que asegurarse de que no aparezca un "cisne negro".
Curiosidades
Un "cisne negro" es un evento de alto impacto, difícil de predecir y muy improbable que suceda, de acuerdo con el conocimiento actual. Su nombre proviene de la creencia en Occidente de que todos los cisnes eran blancos y el evento de encontrar uno negro se consideraba imposible antes del siglo XVII, hasta que se descubrió que existían en Australia.
El algoritmo recursivo para el problema de las torres de Hanoi es óptimo, en el sentido de que es imposible resolver el problema haciendo un número menor de movimientos de anillos. Para demostrarlo una vez más, se utilizará la inducción. Obviamente es óptimo para n = 0. Supóngase que también para n − 1 anillos. Es decir, que es imposible mover n − 1 anillos de una torre a otra en menos de Mov(n − 1) movimientos. Ahora se debe probar que para mover n anillos de una torre a otra, necesariamente hay que hacer 2 × Mov(n − 1) + 1 movimientos.
Considérese algún algoritmo hipotético que lo hace, y obsérvese en el momento justo en el que mueve el anillo mayor a su torre de destino final, por ejemplo la C. En ese momento, los n − 1 anillos restantes deben estar en la torre B, y por la hipótesis de inducción, para moverlos hacia ahí, se tuvieron que haber hecho al menos Mov(n − 1) movimientos. De igual forma, ahora es necesario mover estos anillos a la torre C, para lo cual hacen falta otros Mov(n − 1) movimientos, al menos. Contando el movimiento del anillo mayor, se tiene como resultado que se ejecutaron al menos 2 × Mov(n − 1) + 1 movimientos en total.
Este algoritmo recursivo para el problema de las torres de Hanoi es muy fácil de entender. Sin embargo, no es muy eficiente en cuanto a la cantidad de memoria que utiliza. Se verá más adelante cómo al ejecutar un programa en una computadora, se requiere que ésta tenga memoria para almacenar tanto el programa mismo como los datos que utiliza durante su ejecución. Por ahora sólo se hace notar que el algoritmo recursivo necesita mucha memoria, ya que cuando Arcadio quiere resolver el problema para n anillos, recurre a un amigo a fin de que anote los movimientos para resolver dos problemas de n − 1 anillos; éste a su vez pedirá a otra persona que resuelva dos problemas de n − 2 anillos, y así sucesivamente. La memoria a la que se ha hecho referencia son precisamente estas anotaciones. Así que se han visto dos algoritmos que resuelven el problema de las torres de Hanoi: uno iterativo y otro recursivo, ambos igualmente eficientes en cuanto al tiempo, pero el iterativo más eficiente en cuanto a memoria.
En general, la eficiencia de los algoritmos se mide de acuerdo con la cantidad de recursos que se consumen durante su ejecución. Si interesa determinar la complejidad de un algoritmo que debe lograr que A comunique algo a B, probablemente se desearía medirla en términos del número de mensajes que A debe enviar a B para lograrlo; si cada mensaje tiene un costo implícito, buscaríamos un algoritmo que requiriera la mínima cantidad de mensajes.
Si en cambio se estuviese interesado en un algoritmo que permita que un brazo robótico pinte un automóvil, a lo mejor la complejidad estaría dada en términos del número de movimientos del brazo. En fin, para cada algoritmo existen diferentes recursos susceptibles de cuantificarse; seguramente alguno o algunos de ellos serán los más importantes, según el criterio de quien lo analiza. Ciertamente existen dos recursos consumidos siempre por todo algoritmo: tiempo y memoria.