La siguiente función aparece en análisis de algoritmos cuando una operación se repite una vez, luego dos veces, luego tres, n veces. La función está definida para todo número entero n mayor o igual a 1:
f(n) = 1 + 2 + 3 + … + n
Es decir,
f(1) = 1, f(2) = 1 + 2 = 3, f(3) = 1 + 2 + 3 = 6
etcétera. Resulta que, en general,
f(n) = n(n + 1)/2
y es posible demostrarlo por inducción. Como en cualquier prueba por inducción, se comienza con la base.
Base: para n = 1, se corrobora que f(1) = 1(1 + 1)/2 = 1, lo cual corresponde a la definición de f.
Paso de inducción: supóngase que para un valor de n es cierto que:
f(n) = n(n + 1)/2
Entonces será igualmente cierto para el siguiente valor, n+1. Es decir, se debe probar que:
f(n + 1) = (n + 1) (n + 2)/2
En efecto, por definición,
f(n + 1) es igual a 1 + 2 + 3 + … + n + (n + 1)
Pero en la hipótesis de inducción se asume que los primeros n términos de esta suma, es decir f(n), son iguales a n(n + 1)/2 y, por lo tanto, se les puede reemplazar por este valor:
f(n + 1) = n(n + 1)/2 + (n + 1)
lo cual, con un poco de álgebra, toma la forma esperada:
f(n) = n(n + 1)/2 + 2(n + 1)/2
f(n) = n(n + 1)/2 + 2(n + 1)/2
f(n + 1) = n(n + 1) (n + 2)/2
Una función similar que emplea la multiplicación en lugar de la suma es la siguiente:
f(n) = 1 × 2 × 3 ×… × n
Ésta es la famosa función factorial. El número que resulta de estas multiplicaciones se denomina factorial de n y se denota n!, es decir que f(n) y n! es lo mismo. Por ejemplo, cuando n vale 4, n! = 1×2×3×4=24.Nótese que esta función tiene la misma estructura que la función cuadrática. Ambas pueden ser definidas en términos de sí mismas, de manera recursiva. La forma recursiva es muy elegante y, como cualquier definición de este tipo, consta de dos partes: la base y el caso general.
Para la función cuadrática, se tiene que f(n) = 1+2+…+ (n − 1) + n, pero los primeros n − 1 términos no son más que f(n − 1):
f(n) = f(n − 1) + n
Lo mismo para f (n − 1); ésta es igual a f(n − 2) + n − 1, y así sucesivamente hasta f (1) = 1. Gráficamente se le puede representar mediante un árbol, como el que aparece a la derecha.
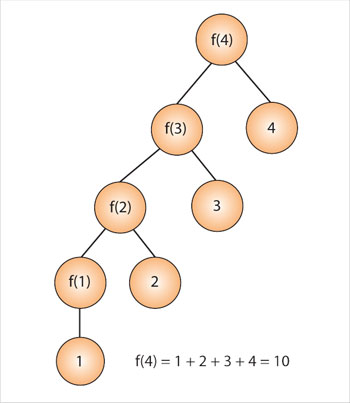
Y para la función factorial:
1! = 1
n! = (n − 1) ! × n
mediante la inducción puede mostrarse que la definición recursiva es igual a la iterativa. Una prueba por inducción de que la definición recursiva es igual a la iterativa para la función factorial es la siguiente:
Base: para n = 1 son iguales. Ambas definiciones dicen que 1! = 1
Paso de inducción: Asúmase que ambas definiciones son iguales para un cierto valor, por ejemplo m. Ahora, se desea mostrar que también lo serán para el que sigue, m + 1. Según la definición recursiva:
(m + 1)! = m! × (m + 1)
Pero se está suponiendo que m! es lo que la definición iterativa plantea, es decir,
m! = 1 × 2 × ... × (m − 1) × m
así que es posible reemplazar esto en la fórmula anterior y obtener:
(m + 1)! = 1 × 2 × ... × (m − 1) × m × (m + 1)
La función exponencial exp(n) se puede analizar de manera similar. Si se admite que es igual multiplicar 2 por sí mismo n veces, que hacerlo por partes (una parte de las multiplicaciones y luego el resto) se obtiene la definición recursiva:
exp(n) = exp(n1) × exp(n2)
donde n1 y n2 son números menores a n, tales que n = n1 + n2, hasta llegar a la base:
exp(1) = 2
exp(0) = 1
Un árbol correspondiente al caso de n = 7 es el siguiente:
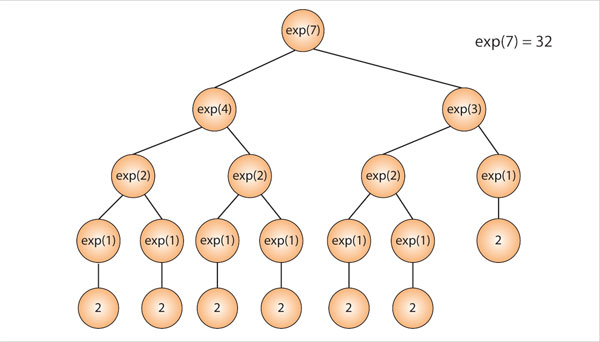
Curiosidades
Una definición circular es aquella donde se expresa el concepto definido, y por lo tanto es inútil. Originalmente se definía el kilogramo como la masa de un litro de agua a la presión estándar y temperatura a la que tiene su máxima densidad (aproximadamente cuatro grados). ¡Pero la definición de presión se expresa en términos del kilogramo! Por esta razón se cambió la definición: un kilogramo es la masa de una cierta pieza de metal en la ciudad de Sèvres.