Inspirados en las fichas de dominó, están los tróminos. Un trómino es una ficha en forma de L, compuesta por tres cuadrados iguales. Se tiene un tablero de 2n × 2n cuadros, uno de los cuales posee una marca. Es posible cubrir todo el tablero, menos el cuadro marcado, con tróminos. El siguiente ejemplo muestra cómo cubrir un tablero de 4 × 4 con cinco tróminos (n = 2), dejando libre el de arriba a la derecha.
Para probar que siempre es posible realizar lo anterior, se usará la inducción. Primero la base de la inducción: se comprueba que para n = 1 se cumple el enunciado:

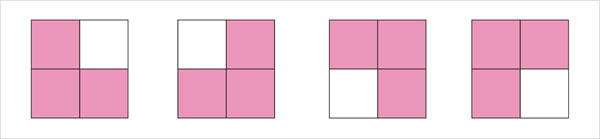
Ahora, el paso de inducción: la hipótesis consiste en suponer que es posible cubrir con tróminos cualquier tablero de 2n × 2n cuadros, uno de los cuales tiene una marca. Posteriormente, se probará que es posible cubrir con tróminos cualquier tablero de 2n+1 × 2n+1 cuadros, uno de los cuales tiene una marca:
Se divide en cuatro cuadrantes iguales, colocando un trómino en el centro:
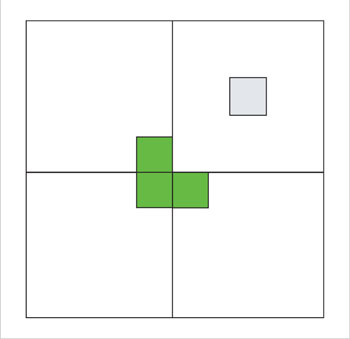
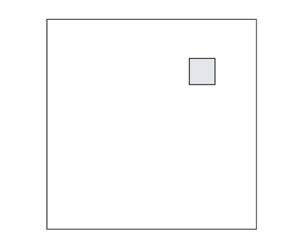
Cada cuadrante es de 2n × 2n y tiene un cuadro marcado, ya sea el original o uno cubierto por el trómino del centro. Por medio de la hipótesis de inducción, existe manera de cubrir cada cuadrante con tróminos; al final queda un solo cuadrado sin cubrir, justo el que estaba marcado originalmente.
Curiosidades
Es posible usar una gráfica para representar un circuito electrónico. Para construirlo y almacenarlo en un chip (circuito integrado) es necesario que no se crucen cables. Con el finde evitarlo, se usan algoritmos muy eficientes que dibujan la gráfica sin que se crucen las aristas, como el inventado por John Hopcroft y Robert Tarjan, dos grandes computólogos que recibieron, por esta y otras contribuciones a la algorítmica, el Premio Turing en 1986.
