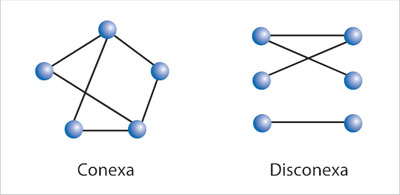
Es claro que la forma de los países no es realmente lo que importa, sino con cuáles comparten frontera. Se puede abstraer la situación dibujando un punto que represente cada país y después conectar dos de ellos mediante una línea, cuando comparten frontera. A continuación se muestran las gráficas correspondientes a los mapas ubicados al inicio de la sección anterior.
Cabe señalar que ya se han usado estructuras de este tipo en el tema 1, en forma de árboles, es decir, sin ciclos (y conexas). Ahora se verán en una versión más general. Las gráficas aparecen por todas partes en computación y en otras disciplinas, ya que sirven para modelar un conjunto y las relaciones entre sus elementos.
En el problema de coloración la entrada es una gráfica y la salida es una asignación de números (llamados colores) entre 1 y k a los vértices, de manera que dos vértices conectados por una arista reciban colores diferentes, y la k sea lo más pequeña posible.
Concepto
Una gráfica es un conjunto de puntos llamados vértices, algunos de los cuales están conectados por líneas llamadas aristas.
"¡Arcadio, no es gracioso!", gritó Úrsula frustrada, al escuchar que éste no tenía aún la lista de invitados de su familia para la boda. "Ya sólo faltan tres meses, no podemos perder más tiempo", le explicó. En sus sueños, Úrsula ya está pensando en la boda, incluso tiene la lista de personas a las que va a invitar; sin embargo, el mayor problema que enfrenta es decidir la cantidad de mesas que deberá alquilar para la fiesta.
Supone que mientras menos mesas alquile, más económica resultará la fiesta, y que además hay mesas de todos tamaños. Es decir, lo ideal sería alquilar una sola mesa, donde se sienten juntos todos los invitados. Desafortunadamente, algunos invitados no mantienen buenas relaciones entre sí y no están dispuestos a sentarse en la misma mesa. Úrsula rápidamente se percata de que tiene que resolver un problema de coloración. Las personas corresponden a vértices, y dos personas tienen una arista si están disgustadas. Cada color representa una mesa, por lo que necesita un algoritmo que coloree a las personas y que utilice el menor número de colores posible. En este momento sonó el despertador y se despertó. Con una sonrisa dibujada en el rostro, corrió al teléfono para contarle a Arcadio su sueño.
Las gráficas que representan países de un mapa tienen la peculiaridad de que se pueden dibujar sin que se crucen las aristas. A estas gráficas se les llama gráficas planas. No todas las gráficas son planas. Por ejemplo, si intentas dibujar una gráfica de cinco vértices, en la que todos los vértices tienen aristas con todos los demás, verás que resulta imposible dibujar sin que se crucen aristas; ésta no corresponde a ningún mapa. Otro ejemplo básico es representar con puntos tres niños, tres niñas y aristas de todos los niños a todas las niñas. Se tienen así las gráficas denominadas K5 y K3,3.
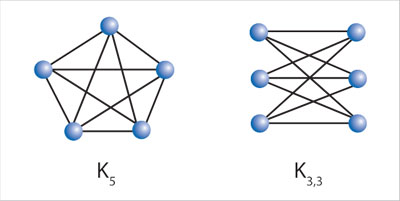
¿Cuántos colores hacen falta para colo-rear K5? Claramente cinco. ¿Y para K6, la gráfica completa sobre seis vértices? Pues seis. Así que, mientras que una gráfica plana siempre se puede colorear con cuatro colores, otras gráficas requieren de un número arbitrariamente grande de colores.
Una gráfica conexa tiene la propiedad de permitir llegar de cualquier vértice a cualquier otro caminando por las aristas. Una gráfica correspondiente a un mapa con dos continentes diferentes sería una gráfica disconexa.
Por lo tanto, hay gráficas de varios vértices que se pueden colorear con un solo color: gráficas sin aristas (disconexas).