En general, el problema de colorear mapas consiste en elegir el color de cada país, de tal forma que siempre que dos países tengan una frontera común, posean colores diferentes (si dos países se tocan en un solo punto no comparten frontera). Esto es muy fácil de realizar, simplemente eligiendo un color distinto para cada país. El problema se complica cuando hay que usar pocos colores.
Hay muchos problemas de coloración que se estudian en matemáticas y cuyas aplicaciones en computación son de gran importancia, más que para colorear mapas para situaciones donde se necesita asignar recursos evitando conflictos. Más adelante se darán algunos ejemplos.
Curiosidades
En 1852, mientras Francis Guthrie intentaba colorear un mapa de los condados de Inglaterra, notó que cuatro colores eran suficientes para lograr su objetivo. En ese entonces Guthrie era estudiante, en la University College de Londres, de Augustus de Morgan, a quien pidió una explicación de por qué aparentemente es posible colorear cualquier mapa con cuatro colores. Así nació un problema que tomó más de 120 años de esfuerzo de muchos matemáticos para resolverlo. En 1976 se logró demostrar, con el auxilio de un programa de computadora que, en efecto, es posible colorear cualquier mapa con cuatro colores.
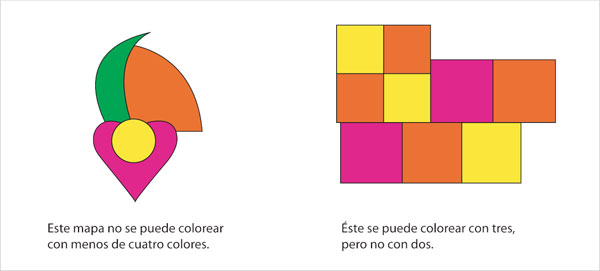
Tomó 123 años probar que cualquier mapa se puede colorear con cuatro colores y la prueba es complicadísima. Es mucho más sencillo demostrar que cinco colores son suficientes, pero aquí se probará algo aún más fácil: que es posible colorear cualquier mapa con seis colores como máximo.
Se analizará si este enunciado se cumple, mediante la técnica de inducción, para cualquier mapa de n países, así como para cualquier mapa de n + 1 países. Primero se abordarán casos pequeños.
Base de la inducción. Obviamente, el enunciado se cumple para mapas de máximo seis países, al designar a cada uno un color distinto.
Paso de inducción. Supóngase que cualquier mapa de n países se puede colorear con seis colores, si se considera que cualquier mapa tiene, necesariamente, al menos un país que comparte frontera con cinco países como máximo.
Lo anterior se puede verificar con algunos ejemplos. Probarlo no es fácil,3 pero vale la pena intentarlo. Tómese un mapa de n + 1 países.
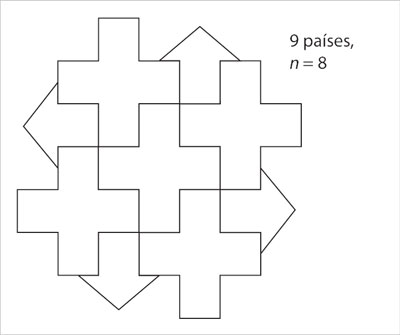
Después, elimínese un país que tenga frontera con cinco o menos países.
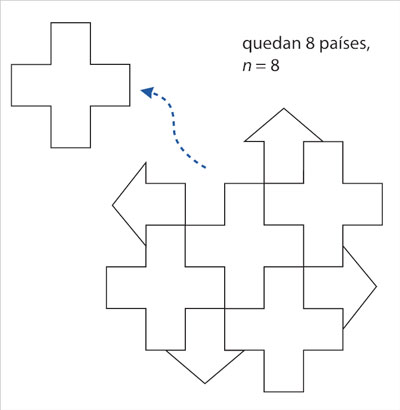
De acuerdo con la hipótesis de inducción, el mapa resultante se puede colorear con seis colores.
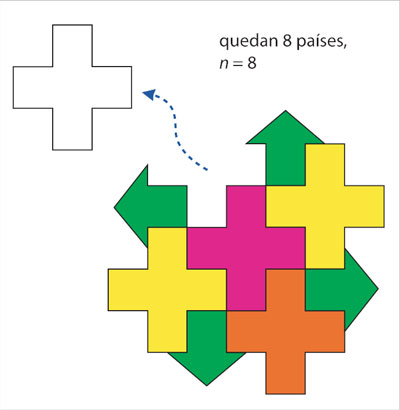
Regrésese el país a su lugar original. Como tiene cinco vecinos, se le puede asignar, de los seis colores disponibles, uno que no use ninguno de sus vecinos.
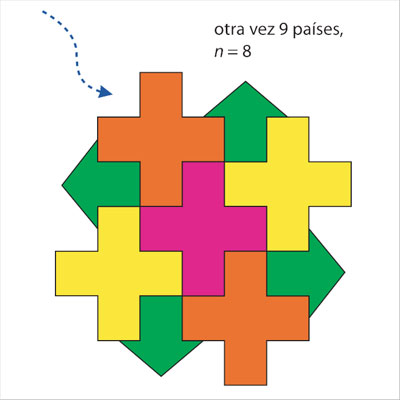
Con esto se ha concluido la prueba de que siempre se puede colorear un mapa con seis colores. Más aún, ahora se tiene una idea de cómo diseñar un algoritmo eficiente para colorear un mapa con máximo seis colores. Un reto interesante es diseñar uno antes de ver el algoritmo propuesto más adelante.