Cualquier receta de cocina requiere ciertos ingredientes para su realización y produce, luego de seguir en orden una serie de instrucciones, el platillo que se desea preparar. Las instrucciones deben seguirse al pie de la letra para lograr el resultado deseado; en este caso, hacer 42 galletas. Un algoritmo consiste en una secuencia finita de instrucciones, que se ejecutan cada vez que se corre el algoritmo, comenzando con los datos que recibe como entrada, y que termina al producir una salida. Cada vez que se corre puede recibir una entrada diferente.
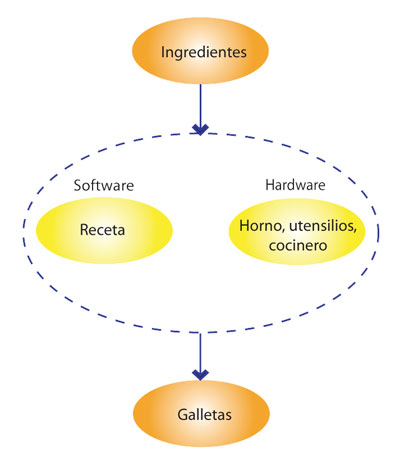
Una receta de cocina es análoga al concepto de algoritmo en computación. Los ingredientes corresponden a los datos de entrada; las galletas juegan el papel de los datos de salida y los pasos de la receta el de las instrucciones del algoritmo, que transforman la entrada en la salida. Lo anterior constituye el software que es ejecutado por una máquina, entendida aquí, en un sentido muy general y abstracto, por Úrsula, su madre, el horno y demás utensilios de cocina. En resumen, el hardware lo constituyen las máquinas ejecutoras del algoritmo de las galletas de la abuela.
Nótese que este algoritmo tiene una sola entrada y produce una sola salida, aunque éstas sean compuestas: la entrada consiste en todos los ingredientes que especifica la receta, y la salida en las 42 galletas. Éste es un tipo básico de algoritmos, aunque los hay de muchos tipos, por ejemplo, los algoritmos en línea. Un algoritmo en línea es aquel que recibe entradas una y otra vez a lo largo del tiempo, y genera las salidas correspondientes. Para aclarar cómo son, pensemos en la fluctuación del valor del peso respecto al dólar y en un algoritmo que monitorea esta relación: tomando una entrada el primer día de cada mes con los tipos de cambio se generan cálculos y se produce una salida, como el cambio promedio en lo que va del año.
La "máquina" que prepara las galletas debe saber qué significa batir las claras de huevo a punto de turrón o tamizar la harina, por ejemplo. Para un hardware diferente, quizá sea necesario dar instrucciones más detalladas, como: "Toma una cuchara, levántala 20 cm, inclínala 20 grados, realiza 35 giros a una velocidad de 15 por segundo, etcétera". O, por el contrario, una receta válida podría ser: "Prepara 42 galletas como las que hacía la abuela", pensada para que la hermana de Úrsula, quien vio a la abuela preparar las galletas muchas veces, la elabore. En otras palabras, las instrucciones deben ser adecuadas para la máquina que las ejecutará.
Esto permite establecer una diferencia importante entre recetas de cocina y algoritmos. La receta nos dice cómo preparar 42 galletas. Si queremos preparar 21 galletas, ¿qué hacemos? Si reducimos todos los ingredientes a la mitad, ¿en realidad saldrán 21 galletas?, ¿reducimos a la mitad el tiempo de horneado?, ¿a qué temperatura poner el horno? y ¿cómo modificamos la receta si requerimos 2 000 galletas para una boda? Inclusive si estamos interesados en exactamente 42 galletas, la receta no nos dice nada acerca de cómo preparar galletas de coco o de chocolate con nuez.
En realidad, la receta para preparar 42 galletas no enseña mucho acerca del arte de cocinar galletas. Si la receta dijera cómo preparar cualquier cantidad de galletas, se parecería más a un algoritmo, que acepta entradas de cualquier tamaño y produce una salida correspondiente. Un algoritmo especial para elaborar galletas diría mucho más acerca del proceso de hacer galletas; por ejemplo, indicaría cuál debe ser la temperatura del horno en función de la cantidad de masa de galletas utilizada, o cuántos huevos se requieren por cada galleta que se desee preparar.
Algunos algoritmos que se utilizan en comercio electrónico y cajeros automáticos son probabilistas. Es decir, incluyen instrucciones que deciden qué acción tomar al azar. Estos algoritmos pueden llegar a fallar, aunque con una probabilidad muy pequeña.
Un ejemplo:
Multiplíquense dos números. Recordar la tabla para multiplicar números del 1 al 9 es muy útil, ya que permite responder a cualquier multiplicación de números en este rango, rápido y sin necesidad de pensar. En este caso, un algoritmo válido para multiplicar 4 × 6 es simplemente regresar el resultado: 24. Sin embargo, saber multiplicar es más cercano a conocer un método como el que se aprende en la escuela, que facilita multiplicar cualquier pareja de números, de cualquier tamaño. Quizá el lector no se haya detenido a pensar lo maravilloso que es esto. Se tiene un algoritmo para multiplicar números arbitrariamente grandes, ¡de miles de billones de cifras! Claro, quizá sería imposible hacerlo porque tomaría millones de años, pero se sabe cómo se haría y que el algoritmo funciona siempre.
Justamente, los algoritmos son fascinantes por estar constituidos por una secuencia de pasos finita, es decir, un algoritmo debe tener un cierto número de instrucciones. En el caso de una receta para hacer 42 galletas probablemente esto no sorprende, pero en el caso de un algoritmo que debe funcionar para cualquier tamaño de entrada, sí. Esto hace que un algoritmo aporte mucha información acerca del problema.
Si se tuviese a disposición un número infinito de instrucciones, un algoritmo para multiplicar dos números consistiría en una tabla de multiplicar infinita, y para calcular el producto de dos números respondería con el valor correspondiente de la misma tabla de multiplicar. Una tabla infinita como ésta no nos dice mucho acerca de la operación (multiplicación); de hecho, se podría resolver cualquier problema de esta forma con tan sólo una tabla infinita que para cualquier entrada indicara una salida válida al problema.
Un algoritmo es un procedimiento que puede seguirse mecánicamente, con el hardware adecuado, sin necesidad de interpretaciones, es decir, sin pensar qué hacer a cada momento. Por tanto, es importante que no exista ambigüedad en la interpretación de las instrucciones. Los términos usados deben significar exactamente lo mismo para cualquiera que lleve a cabo la receta. Lo anterior no significa que los algoritmos sólo hagan cosas sencillas; también hay los que juegan ajedrez al nivel de los mejores jugadores del mundo. Más aún, el que las instrucciones de un algoritmo deban estar exentas de ambigüedad, no significa que no se permita algo de libertad al cocinero. Un algoritmo puede incluir una instrucción no determinista que diga: "elige un número entre 1 y 10". Incluso podría incluir una instrucción probabilista, como indicar que se elija cualquiera de estos números con la misma probabilidad. Para algunos problemas, los mejores algoritmos son probabilistas, especialmente para criptografía. Más adelante se mostrará un algoritmo probabilista para ordenar números rápidamente. Pero cabe enfatizar que, aun cuando una instrucción pueda devolver distintos resultados, no debe existir ambigüedad en cuanto a su especificación.

Michael O. Rabin
(1931) Galardonado con el Premio Turing en 1976, ha contribuido, entre muchas cosas, con la introducción del concepto de no determinismo, así como con algoritmos probabilistas muy importantes, como el que determina si un número es primo y el criptosistema, que lleva su nombre