¿Qué puede ser peor que un problema exponencial? ¡Un doble exponencial! Es decir, tomar la función 2n y en lugar de la n poner 2n para obtener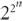 
, o sea que, en lugar de multiplicar el número 2n veces por sí mismo, hay que multiplicarlo 2n veces por sí mismo. Es difícil darse una idea de lo rápido que crece esta función. Para n = 5 el valor de la función rebasa los 4 000 millones, mientras que en n = 7 el valor de la función rebasa el número de microsegundos que han pasado desde el Big Bang.
Curiosidades
La pregunta P = NP es la más importante en computación, y en general una de las más importantes en matemáticas. En efecto, el Instituto Clay de Matemáticas la ha catalogado entre los siete problemas para celebrar las matemáticas del nuevo milenio.
Existen problemas que requieren de este tiempo para resolverse. Por ejemplo, algoritmos que deciden si un enunciado es falso o verdadero, cierto formalismo lógico en el cual se pueden hacer enunciados de los números enteros de la forma:
Si x = 16, entonces no existe un número y, tal que y + y + y = x
Asimismo, existen problemas que requieren un tiempo triple, cuádruple o quíntuple exponencial. Y por si fuera poco, existen problemas más difíciles que cualquiera de éstos. De hecho, para cualquier problema que se le ocurra a una persona, existe siempre uno todavía más difícil.
Curiosidades
La pregunta P = NP es la más importante en computación, y en general una de las más importantes en matemáticas. En efecto, el Instituto Clay de Matemáticas la ha catalogado entre los siete problemas para celebrar las matemáticas del nuevo milenio.
