Una vez segmentada la imagen es posible extraer las regiones u objetos de la misma, los cuales corresponden a objetos en dos y tres dimensiones. Además, dependiendo de la imagen de procedencia, pueden ser curvas, superficies o sólidos.
Hay diferentes sistemas de coordenadas: cartesianas (rectangulares), polares, esféricas, cilíndricas, entre otras. Cada una de estas representaciones tiene ventajas y desventajas, por lo que deben seleccionarse de acuerdo con las necesidades del problema de estudio.
En la práctica, el sistema de coordenadas cartesianas es muy útil para determinar, por medio de dos números, cualquier punto en el plano. Para definir estas coordenadas se utilizan dos líneas perpendiculares dirigidas: el eje de las x y el eje de las y, así como una unidad de longitud, usualmente enteros. Pero, ¿para qué sirven los sistemas de coordenadas en este contexto? A través de un sistema coordenado, podemos describir figuras geométricas, utilizando ecuaciones algebraicas, es decir, ecuaciones que son satisfechas por los puntos en la figura.
Es importante considerar que cuando se diseñaron las representaciones de curvas por medio de coordenadas no se contaba con computadoras. En la actualidad se cuenta con representaciones nuevas, basadas en las anteriores, pero con un enfoque computarizado. Por ejemplo, para las imágenes digitales todo se mide en múltiplos de pixeles, en cantidades enteras.
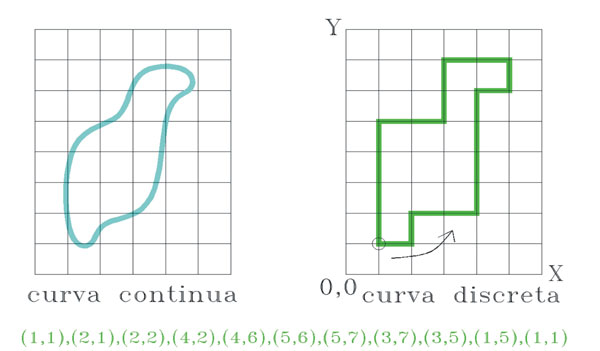
Cualquier curva puede digitalizarse y representarse por medio de sus coordenadas. La figura 7 muestra un ejemplo de una curva continua y su digitalización. Sus coordenadas son introducidas a la computadora y después desplegadas en un dispositivo de salida. Es importante que las representaciones sean compactas, que permitan la transferencia de información con facilidad y que sean lo más estándar posible para su incorporación a diferentes sistemas. Las representaciones interesantes de curvas, si se considera lo antes mencionado, corresponden a los llamados códigos de cadenas.
René Descartes
(1596-1650). También conocido como Renatus Cartesius, fue un filósofo, matemático, científico y escritor francés. Se le considera el "padre de la filosofía moderna" e, incluso, "padre de las matemáticas modernas".
Curiosidades
(Si se calculan todas las combinaciones de los elementos de las cadenas de Freeman, digamos de 10 elementos, y sólo se consideran las formas cerradas sin cruces internos e invariantes a la rotación, se obtendrán todas las formas cerradas a esa resolución.
En 1961, el profesor Herbert Freeman 1 de la Universidad Rutgers propuso un método para representar curvas o contornos de regiones en el plano a través de un código de cadenas. En la figura 8(a) se aprecian las diferentes direcciones de los elementos de las cadenas de Freeman. Los elementos van del 0 al 7: los elementos 0, 2, 4 y 6 tienen una longitud de uno; y los elementos 1, 3, 5 y 7, una longitud de √2. Todas sus posiciones son discretas, es decir, inician y terminan en un vértice de la cuadrícula. De ahí que cualquier curva en el plano, ya sea abierta o cerrada, se pueda representar usando este código.
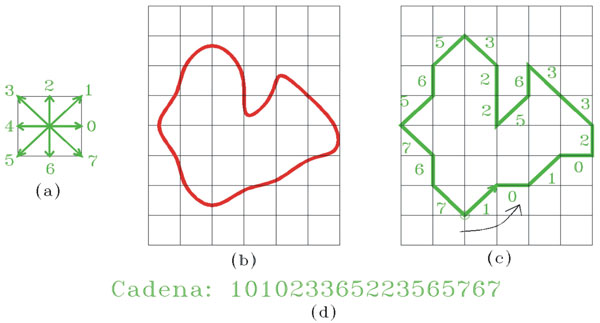
La figura 8(b) presenta un ejemplo de una curva continua en el plano; en (c) se muestra su versión digital en una resolución previamente definida, es decir, al tamaño del cuadro considerado. Es fácil notar que los vectores de las cadenas de Freeman se aproximan lo más posible al contorno debido a su cercanía con los vértices de la cuadrícula. Como se puede observar, la curva discreta mostrada en la figura 8(c) está compuesta por 18 segmentos de línea recta y representada por la cadena: 101023365223565767.
El origen de la curva en la figura 8(c) está representado por una pequeña circunferencia. Con la información de la cadena, las coordenadas (x,y) del origen de la curva y el tamaño de la cuadrícula es posible reconstruir la curva discreta sin perder información.
Una característica importante de este código, que se puede observar directamente, es su capacidad de compresión sin pérdida de información. Si se representa cada elemento de la cadena por tres bits, los ocho elementos de la cadena en forma binaria quedarían como: 000, 001, 010, 011, 100, 101, 110 y 111, respectivamente. Lo anterior proporciona una forma compacta de representar formas de objetos o curvas.
En 1999, en la Universidad Nacional Autónoma de México se desarrolló el código de cadenas de vértices (Vertex Chain Code, VCC ).2 Este código de cadenas se basa en el principio de imágenes digitales. Cada objeto o región está compuesto por un número finito de pixeles conectados unos a otros. Si la imagen usa pixeles cuadrados, el VCC utiliza conectividad 4 (aunque también es posible utilizar celdas triangulares o hexagonales), como se muestra en la figura 9.-
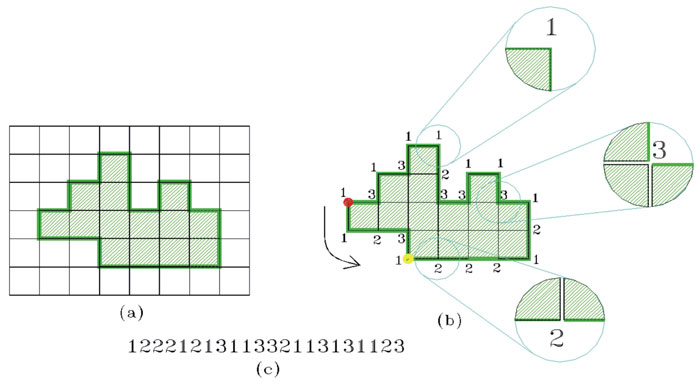
El VCC representa el número de vértices de los pixeles en la forma en que tocan el contorno de la región. Observa la figura 9: en (a) se tiene un ejemplo de región compuesta de 14 pixeles. Los elementos del VCC aparecen en (b), donde es fácil apreciar que el elemento 1 corresponde a un vértice que toca un pixel del contorno; el 2 corresponde a dos vértices de dos pixeles, y el 3 a tres vértices de tres pixeles de la región. En esta forma, se generan los elementos del VCC para cualquier región.
La figura 9(c) muestra la cadena considerando el origen (representado por un punto) y sentido indicado por la flecha, lo que produce la cadena: 1222121311332113131123. Es importante resaltar que esta cadena no se basa en símbolos, como en el código de cadenas de Freeman, que bien podrían ser letras o números. En el VCC los elementos de la cadena indican propiedades intrínsecas de la forma que representan; nos señalan el número de vértices que toca el contorno: ¿cuántos son rectos?, cantidad de los 2; ¿cuántos son cóncavos?, cantidad de los 3; ¿cuántos son convexos?, cantidad de los 1. Así, el VCC permite tener un descriptor de forma que indica las propiedades geométricas de ésta.
Es conveniente tener siempre una misma cadena para cada forma o región. Arbitrariamente se seleccionó un punto como origen. Sin embargo, ¿qué hubiera pasado de haber seleccionado otro origen? Se produce otra cadena. Para generar una cadena independiente del origen se recomienda seleccionar el origen que corresponda a la cadena mínima. Cada origen diferente alrededor de la curva genera una cadena distinta. Entonces, se considera a cada cadena como un número entero y se selecciona aquella que representa el número menor. En caso de que existan dos cadenas mínimas iguales, se deberá agregar una definición más para describir un origen único.
La cadena en la figura 9(c) está compuesta por 22 elementos. De esta manera, se generan 22 cadenas, las cuales se presentan a continuación:
1222121311332113131123
2221213113321131311231
2212131133211313112312
2121311332113131123122
1213113321131311231222
2131133211313112312221
1311332113131123122212
3113321131311231222121
1133211313112312221213
1332113131123122212131
3321131311231222121311
3211313112312221213113
2113131123122212131133
1131311231222121311332
1313112312221213113321
3131123122212131133211
1311231222121311332113
3112312221213113321131
1123122212131133211313
1231222121311332113131
2312221213113321131311
3122212131133211313112
De todas estas cadenas se selecciona la de menor valor y ésa es la que representa la región invariante al origen. Esta cadena se indica con números en negritas. Igual que en el código de cadenas de Freeman, en el VCC se puede obtener una importante capacidad de compresión sin perder información. Si se representa cada elemento de la cadena para una celosía de cuadros en forma binaria, se obtiene para sus tres elementos: 01, 10 y 11, respectivamente. Sólo se emplean dos bits para representar cada uno de los elementos de la cadena.
Ahora se tratará la representación de las curvas en el espacio o tridimensionales (curvas 3D). La representación de curvas 3D es un tópico de gran importancia en diferentes áreas del conocimiento, ya que se presentan de manera natural en muchas situaciones, como por ejemplo en la trayectoria que describe un avión o un pájaro al volar, la doble hélice de la cadena del ADN, la trayectoria que describe una planta como la enredadera, etcétera.
Como se mencionó anteriormente, una es curva una configuración unidimensional, y una forma natural de representarla es por medio de sus coordenadas cartesianas, sólo que ahora se utilizarán tres ejes de referencia: x, y, z. Cualquier curva 3D puede ser digitalizada y representada en forma discreta. La figura 10 ilustra un ejemplo de una curva cerrada en 3D.
Para digitalizar curvas 3D es necesario intercalarlas en una cuadrícula tridimensional. Si se toma la secuencia de los puntos de la curva y se codifican los vértices de la cuadrícula más cercanos a la curva, se obtiene su digitalización. El tamaño del segmento de la cuadrícula define la resolución que se desea para la curva. Una vez digitalizada la curva se obtienen los valores discretos de la misma, es decir, si está en Z3 (Z es el conjunto de los números enteros). Dentro de la cuadrícula 3D los pasos siempre caen en los vértices de la misma, no en posiciones intermedias. La figura 11 muestra la versión discreta de la curva representada en la figura 10.
Curiosidades
A las curvas 3D representadas en este libro se les ha dado un grosor, es decir, son mostradas como cuerdas. Esto proporciona una mejor visualización y comprensión: se puede ver su profundidad y otras características.

Al igual que en la representación de dos dimensiones, se han encontrado importantes ventajas en la representación de curvas 3D por medio de códigos de cadenas, puesto que son una forma simple de almacenamiento de información y de compresión. Los códigos de cadena se han vuelto un estándar para muchos algoritmos de análisis de forma de objetos. Aquí se muestra el código de cadenas de cambios de dirección ortogonal,3 llamado código de cadenas 3D.
Este código se presenta en la figura 12:(a) ejemplo de curva 3D continua; (b) versión digitalizada de curva 3D, constituida por segmentos de línea recta, todos ellos en posiciones ortogonales. Esta curva digitalizada está compuesta de 10 segmentos. Las figuras (c)-(g) muestran los diferentes elementos de la cadena para cada cambio de dirección.
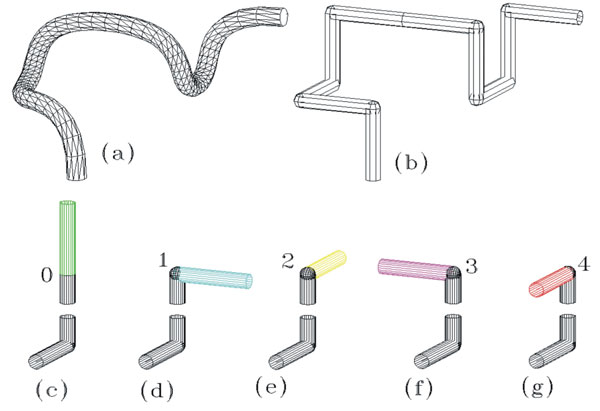
Con sólo cinco elementos4 de cadena podemos representar cualquier curva discreta. No está permitido ir y regresar por el mismo segmento de línea recta. Cada cambio de dirección está formado por dos segmentos de línea recta contiguos, y cada elemento de cadena por dos cambios de dirección; es decir, siempre se necesitan las dos direcciones anteriores de los segmentos de recta para definir el actual. Con el fin de facilitar la comprensión de los diferentes cambios de dirección, se han asignado colores a cada uno de ellos. Así, los elementos de la cadena para representar cualquier curva discreta 3D están definidos como sigue:
1] El elemento de cadena 0 indica que no hay cambio de dirección del último segmento, es decir, que sigue en línea recta. Está representado en la figura 12(c) con el color verde.
2] El elemento 1 indica un cambio de dirección hacia la derecha, a partir del cambio de dirección anterior. Se muestra en la figura 12(d) con el color cian.
3] El elemento 2(e) indica un cambio de dirección tipo escalera y se muestra con el color amarillo.
4] El elemento 3(f) indica un cambio de dirección hacia la izquierda, a partir del cambio de dirección anterior, con el color magenta.
5] El elemento 4 describe un cambio de dirección de regreso, de vuelta en U, como se ilustra en la figura 12(g) con el color rojo.
La figura 13 muestra cómo asignar los elementos a una curva.
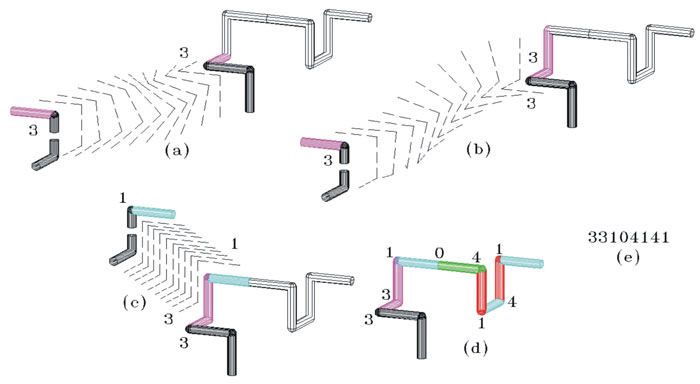
El la figura 13(a), el origen de la curva se localiza en la parte baja. Ahora supóngase que se camina sobre la curva, al estar frente a un ángulo recto ¿cuál es el siguiente paso? Hacia la izquierda, por lo tanto le corresponde un 3, o sea, el color magenta. Los dos primeros segmentos al iniciar la curva no son etiquetados, debido a que sirven de referencia para definir el primer elemento, es decir, el 3. En la figura 13(b), para calcular el siguiente elemento de la cadena se toman como referencia, de nuevo, los dos elementos anteriores; se camina sobre la curva otra vez, se va hacia la izquierda, por lo que le corresponde un 3 (magenta). La figura 13(c) muestra el siguiente elemento de la curva, sólo que ahora se gira hacia la derecha y le corresponde un 1 (cian).
Finalmente, en la figura 13(d) se muestran todos los elementos de la cadena. Es importante notar que cuando existe un 0 es necesario ver cuál fue el último cambio de dirección diferente de este número para definir el elemento actual. Cuando se encuentra un 0 como en el ejemplo propuesto, se busca el anterior para definir el actual; en este caso se forma un 4, o sea el color rojo. La cadena está compuesta de los siguientes elementos: 33104141.
Para el caso de curvas abiertas, el número de segmentos de la curva siempre es el número de elementos de la cadena más dos, ya que los dos primeros se utilizan como referencia. La secuencia en colores de la cadena mencionada es la siguiente: magenta; magenta, cian, verde, rojo, cian, rojo y cian.
La figura 14 muestra dos ejemplos de curvas, utilizando los colores del código de cadenas3D. Una esfera indica el origen de la curva abierta, mostrada en el lado izquierdo de la figura. Hay que recordar que los primeros dos segmentos siempre se usan como referencia. Esta curva abierta está compuesta de 40 segmentos de línea recta, o sea, de una cadena de 38 elementos.
La curva cerrada está representada por 24 segmentos de línea recta y por 24 elementos de cadena. En el caso de las curvas cerradas, tanto el número de segmentos de línea recta como el número de elementos de la cadena son iguales. Esto se debe a que siempre se pueden apreciar los dos cambios de dirección anteriores (diferentes de 0) para definir el cambio presente. El origen de la curva abierta se representa también por una esfera, y la dirección de la codificación se da en dirección al segmento verde contiguo.
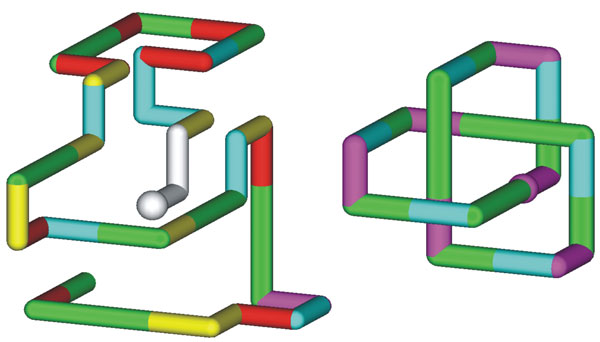
Al igual que en el VCC, esta notación puede ser invariante al origen de construcción, al transformar las cadenas a números enteros, recorrer todos los posibles orígenes alrededor de la curva y seleccionar la cadena de menor valor. Para curvas abiertas, sólo hay dos orígenes y se debe seleccionar el que produzca el entero de menor valor.
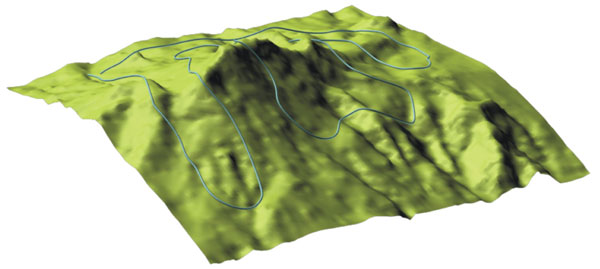
Un ejemplo donde se aplicó el código de cadenas 3D es la representación de la trayectoria de un avión volando sobre el volcán Iztaccíhuatl (véase la figura 15).
Otra aplicación importante de este código ha sido la descripción de algunas curvas matemáticas conocidas, como la curva de Hilbert.5 Esta curva es famosa porque posee un patrón, parecido a una silla de montar, que se repite y va cubriendo el espacio que la contiene en sus diferentes etapas. La figura 11 muestra una de las etapas de la curva de Hilbert; en este caso, para no saturar la imagen con colores, sólo se trazó con uno. Está compuesta de 512 elementos de cadena, los cuales son:
43334114341143341432421434114334
14334114341143341432421434114333
41114334143242143411433414334114
34114334143242143411433414334112
42334114341143341432421434114334
14334114341143341432421434114333
41114334143242143411433414334114
34114334143242143411433414334111
43334114341143341432421434114334
14334114341143341432421434114333
41114334143242143411433414334114
34114334143242143411433414334112
42334114341143341432421434114334
14334114341143341432421434114333
41114334143242143411433414334114
34114334143242143411433414334111
Para ilustrar el potencial de este código, también se generó el siguiente estado de la curva de Hilbert, el cual se muestra en la figura 16. En cada estado, la curva se incrementa en un factor de 8; en este estado la curva contiene 4 096 elementos. Al igual que en el ejemplo anterior, para no saturar la imagen con colores, sólo se utilizó uno. Se observa que esta curva es abierta y la anterior es cerrada. Ambas versiones de curvas se pueden usar.
Una ventaja muy importante de este código es su nivel de compresión de información, ya que sólo requiere 3 bits para representar cada elemento de la cadena, es decir: 000, 001, 010, 011 y 100 para representar los elementos 0, 1, 2, 3 y 4, respectivamente.
Finalmente, este código se ha usado para generar familias de curvas con distintas resoluciones, es decir, con un número de elementos diferente. Por ejemplo, si se desea conocer todas las curvas de 3 elementos, se calculan todas sus combinaciones: 000, 001, 002, 003, 004, 010, 011, 012, 013, 014, 020, 021, 022, 023, 024, 030, 031, 032… y así sucesivamente.
Actualmente, la UNAM posee el récord mundial en la generación de la familia completa de todas las curvas 3D compuestas de 24 segmentos: 282,429,536,481 curvas.6 El récord anterior fue para la familia completa de curvas de 20 segmentos, citado por Brian Hayes en su artículo "Square Knots" en la revista American Scientist.7
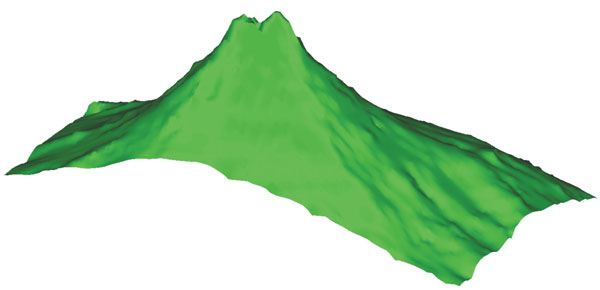
Cuando una imagen se segmenta es posible extraer los objetos de la misma. Una forma común de representar un objeto es por medio de su superficie. La figura 17 muestra el modelo del volcán Popocatépetl. Aunque se trata de un sólido, una forma de representarlo es a través de la superficie que lo envuelve.
Concepto
Rendering es el proceso mediante el cual se genera una imagen a partir de un modelo, utilizando programas de cómputo. El modelo es, como se ha mostrado aquí, la descripción de un objeto tridimensional.
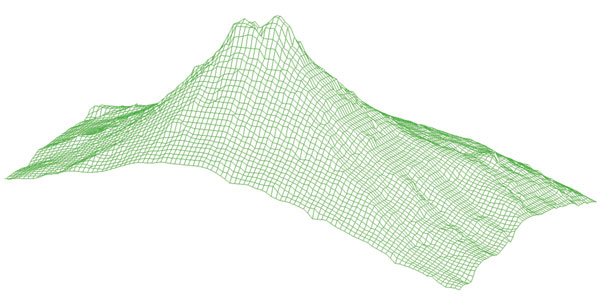
Una forma matemática para representar superficies es por medio de matrices; una matriz es un arreglo rectangular de números. Se coloca una red o malla (la resolución de la red se define previamente) sobre el modelo, como se ilustra en la figura 18. Esta malla tiene un espaciamiento previamente definido; está compuesta de 100 × 70 elementos y cada nodo de la red representa una altura en ese punto del modelo. Por supuesto, a mayor número de elementos, mayor precisión.
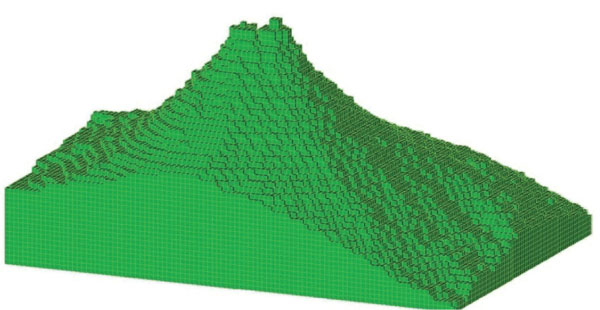
Además de la superficie envolvente que se mencionó arriba, otra manera común de representar sólidos es por medio de "rebanadas"; es decir, a través de la obtención de cortes de imágenes del sólido, tomando en cuenta un incremento constante en cada uno de los cortes. Al unir los cortes se obtiene un modelo tridimensional del objeto de estudio.
Cada uno de los cortes representa el objeto de estudio por medio de pixeles. Si se considera el incremento del siguiente corte igual a la longitud de uno de los lados del pixel, entonces se obtiene un voxel (volume element en inglés) y tiene una forma cúbica. Finalmente, el sólido queda representado por un conjunto de voxeles conectados entre sí. La figura 19 muestra el volcán Popocatépetl representado por voxeles.
Curiosidades
La tomografía es la obtención de imágenes, por secciones, de algún objeto. Este método se utiliza en varias disciplinas: medicina, arqueología, biología, geofísica y ciencia de materiales, entre otras. La palabra tomografía viene del latín tomos, que significa "sección" o "corte", y grafía, que quiere decir "representación gráfica".
Curiosidades
Las medidas de las estructuras cerebrales han probado ser de gran utilidad para la determinación de cambios relacionados con las patologías cerebrales, tales como: esquizofrenia, efecto de fármacos en desórdenes bipolares y cambios relacionados con la vejez.
La forma de almacenar este modelo es por medio de matrices 3D. En este caso, sólo existen dos valores para los elementos de la matriz: el 0 y el 1; el 0 indica ausencia de materia y el 1 indica presencia de materia. Esta forma de almacenar la información tridimensional tiene ventajas, como la fácil obtención de cortes del modelo, así como su volumen y algunas otras características.
Una desventaja de esta representación es la cantidad de información redundante que contiene el modelo, en contraste con la notación de la superficie envolvente. En la notación de la superficie envolvente no existe redundancia en la información, sólo se almacenan las coordenadas de la superficie. Sin embargo, la notación de las superficies se complica cuando existen concavidades en el modelo, debido a que para cada una hay que generar una nueva superficie y, si se desea calcular el volumen total del sólido, hay que restar las superficies de las con-cavidades a la superficie envolvente del sólido.
La figura 20 muestra una importante aplicación de la representación por medio de voxeles; ilustra la materia gris de un cerebro humano compuesta por 876 224 voxeles. En este caso, cada voxel equivale a un milímetro cúbico de materia gris. Esta notación facilita la cuantificación del volumen de la materia gris y el cálculo de su superficie.
