Sin importar el tipo de sensor utilizado para obtener la imagen, es necesario almacenarla y representarla de alguna manera; para esto, existen diferentes maneras de describir dicha imagen. A continuación se detallan las más comunes y sus principales usos.
Una de las formas más comunes para describir imágenes es utilizar números: posición y tamaño de formas geométricas, ya sean líneas, rectángulos, círculos y curvas. A este tipo de imágenes se les denomina imágenes de vector; en ellas está almacenada toda la información geométrica del objeto de estudio: sus coordenadas. Esto permite cambios de escala fácilmente, de ahí que sea el formato preferido por los diseñadores y arquitectos que usan software asistido por computadora como apoyo para sus diseños. Para representar curvas se utiliza un sistema coordenado o espacio de usuario, llamado así porque es el lugar donde los usuarios pueden colocar y relacionar entre sí los elementos de la imagen.
Una imagen en formato raster es una rejilla rectangular de pixeles. Este formato presenta varias ventajas y se usa bastante. Pero es importante resaltar que no se trata de un formato sólido para cambios de escala, ya que los cambios que se realicen deben ser en múltiplos de pixeles, pues los valores intermedios ocasionan pérdida de información.
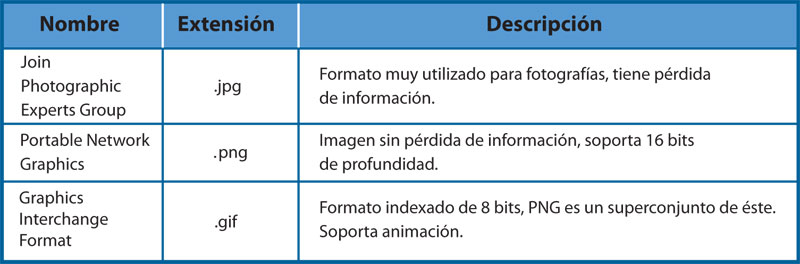
Existe una gran variedad de formatos de archivos para almacenar imágenes raster o bitmap. En la tabla 1 se muestran los más comunes con una breve descripción:
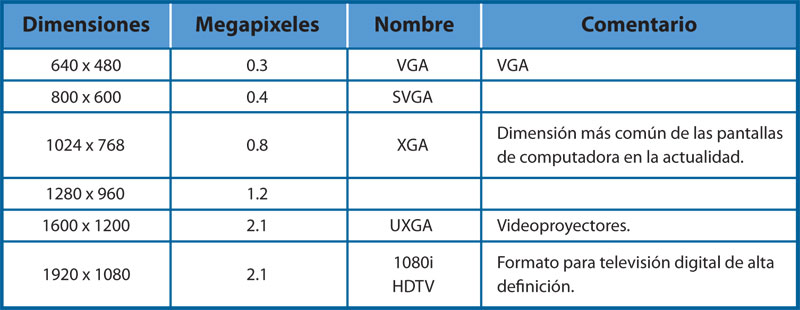
¿De qué tamaño es una imagen digital? Si se piensa en una imagen como una matriz de pixeles, entonces una imagen digital de 2 048 × 1 535 tiene 3 143 680 pixeles o aproximadamente tres megapixeles. Por ejemplo, la buganvilia de la figura 3 es una imagen de 640 × 480 = 307 200 pixeles o 0.3 megapixeles. En la tabla 2 se muestran resoluciones típicas; algunas son utilizadas en televisiones, en monitores o en cámaras fotográficas y de video caseras.
Curiosidades
La mayoría de las imágenes digitales se comprimen. Existen varios tipos de compresión, con o sin pérdida de información. ¿Quién en su sano juicio querría perder información (o sea, los detalles) en una imagen? Resulta que el ojo humano puede esconder o ignorar imperfecciones y, por eso, aunque se quite detalle a las imágenes, el cerebro prácticamente no lo detecta. JPG, uno de los formatos más utilizados, tiene pérdidas de información.
El valor de los pixeles se almacena en la memoria de la computadora; por lo tanto, la información se guarda de manera binaria y la continuidad espacial de la imagen se aproxima por los espacios en la malla de color (sample depth). Esto se conoce como profundidad de color, y existen varias profundidades muy utilizadas:
• 8 bits. Esta profundidad utiliza enteros de ocho bits, que pueden representar hasta 256 valores: 28 = 256. Representan los niveles de brillo.
• 12 bits. Para imágenes muy detalladas, tanto en brillo como en sombras. Algunas cámaras digitales, sobre todo las profesionales, utilizan el formato raw, que es de 12 bits y soporta 212 = 4 096. Permiten gran precisión para almacenar la imagen sin perder detalle.
• 16 bits. La mayoría de los programas para manipulación de imágenes y los formatos comunes PNG y TIF realizan operaciones a 16 bits en imágenes de ocho bits para evitar perder información.
Existen otras profundidades que poseen mayor precisión, pero que se utilizan en aplicaciones muy especiales, como el cine. Por supuesto, la precisión y forma de representación de estas profundidades implica un costo. Las imágenes bitmap utilizan mucho espacio en memoria. Por ejemplo, una imagen de 2.1 megapixeles a colores —con el modelo RGB en ocho bits— utiliza: 1 600 × 1 200 × 3 bytes = 5 760 000 bytes = 5.7 megabytes.
Concepto
En matemáticas, el concepto de curva intenta capturar la idea intuitiva de un objeto continuo y unidimensional. En el estricto sentido, aunque esto ya no parezca obvio, una línea recta también es una curva.