Con frecuencia se escucha hablar en los noticiarios de crecimiento exponencial para enfatizar que algo crece rápidamente. Hasta ahora se ha visto que el crecimiento exponencial tiene un significado preciso. Ocurre cuando se tiene una función de la forma f (n) = cn para algún número c. Nótese que, al principio, el factor tiempo no crecía atropelladamente; por ejemplo, en la tabla 4, con los pocos regalos que había escogido Arcadio, el tiempo aún no se disparaba. Hasta los ocho regalos, Arcadio todavía podía lidiar con el problema en menos de una hora. Incluso 10 regalos implicaron menos de tres horas. Sin embargo, como indica la gráfica 1, alrededor de los 18 regalos la función se dispara.
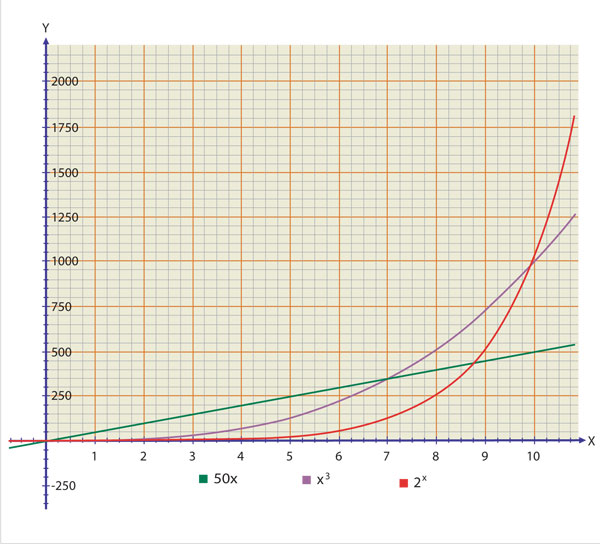
El crecimiento exponencial se puede caracterizar por la velocidad a la que crece el valor de una función. En la gráfica 2 se muestra una función lineal, cuya velocidad de crecimiento es constante, es decir, es la misma en cualquier momento. Se trata de una línea recta y su inclinación o pendiente siempre es la misma. En cambio, en una función exponencial, la velocidad de crecimiento es en sí exponencial, es decir, su valor crece a una velocidad proporcional al valor de la función. En el caso de 2 n la tasa de crecimiento es 2, se duplica su valor con el tiempo. O sea que mientras más grande es la cantidad, más rápido crece. Y tarde o temprano el valor de la función se dispara. En la gráfica también aparece la función n3, cuya velocidad de crecimiento ya no se mantiene constante como en el caso de la función lineal. Aunque crece rápidamente, después de cierto valor (n = 10) será rebasada por la función exponencial.

Curiosidades
Cada número de Fibonacci es la suma de los dos anteriores 1, 1, 2, 3, 5, 8, 13, 21… Se les encuentra frecuentemente en la naturaleza, en particular en terrenos como el del crecimiento poblacional, con un crecimiento de 1.618n aproximadamente. Imágenes como ésta se generan a partir de ellos.
Concepto
Una función f (n) es lineal si es de la forma cn, para alguna constante c, quizá más otra constante. Por ejemplo, f (n) = 3n – 5.