Aunque se han tocado aspectos de la comunicación en general, se aprovechará la agradable distracción que proporciona la causalidad para hablar de otros tópicos relacionados y que, desde la vista del computólogo, involucran conceptos fundamentales. Para comenzar, una historia:
Hace mucho tiempo, el sultán turco inició la invasión del Imperio Bizantino. El emperador, al enterarse de tan terrible noticia, ordenó a sus ejércitos que salieran al paso de los invasores desde distintos puntos. Cada ejército estaba dirigido por un general.
Los ejércitos de Constantinopla que habrían de repeler la invasión turca eran suficientemente poderosos, pero tenían que coordinar sus acciones: todos atacaban o todos se retiraban simultáneamente. Avanzaron entonces con paso firme hasta rodear al ejército turco y los generales pasaron la noche en vela, considerando si debían ordenar el ataque al amanecer. Como había sido acordado previamente, los generales debían tomar una decisión de consenso sobre si atacar o no a los turcos, de manera que por la noche cada uno de ellos envió mensajeros a todos los demás.
La riqueza de los turcos no tenía límites y los bizantinos eran famosos por traidores, así que el problema con el plan de los generales es simple: algunos generales podían haber sido sobornados por el sultán turco. ¿Cómo pueden saber los generales leales si todos atacarán o se retirarán, a pesar de que algunos generales traidores mientan? Si unos atacan y otros se retiran, las consecuencias serían desastrosas.
Este problema se analizará por casos, ¿es posible ponerse de acuerdo con sólo tres generales? Suponiendo que sólo hay un traidor, en la figura 1 sería el que está pintado de verde, el 1. Para simplificar, considérese que el general 1 siempre es el general supremo de los bizantinos y a él corresponde dar la orden inicial. ¿Pueden los generales 2 y 3 saber sin lugar a dudas lo que deben hacer? No, no es posible, y sin importar cuál de los tres generales sea el traidor, siempre sucedería algo similar.
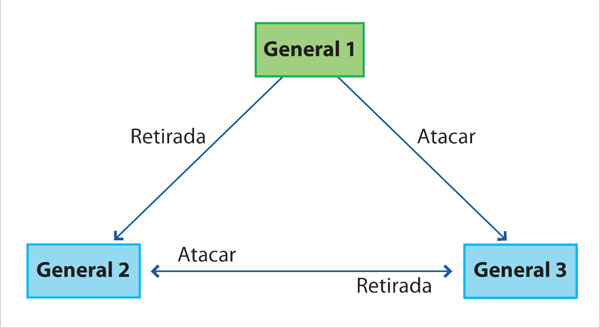
Cada general recibe exactamente dos órdenes, pero como una proviene del traidor ambas serán contrarias entre sí, una es ataque y la otra retirada, de tal suerte que no hay manera de saber cuál está mal. ¿Qué sucede si hay cuatro generales? En este caso, sí sería posible alcanzar una decisión de consenso, ya que los generales leales reciben más mensajes correctos que espurios, como puede apreciarse en la figura 2, donde se supone que el traidor es el general 4, pues envía órdenes contrarias a los demás, es decir, de retirada. Pero no es grave, porque los demás generales reciben dos órdenes de atacar y solamente una de retirarse, por lo que se suman a la mayoría.
En general, se puede demostrar que puede lograrse consenso cuando hay t traidores si existen G número de generales, tal que G > 3t. En el ejemplo se cumple cuando G = 4 generales y t = 1 traidor, ya que 4 > 3 × 1.
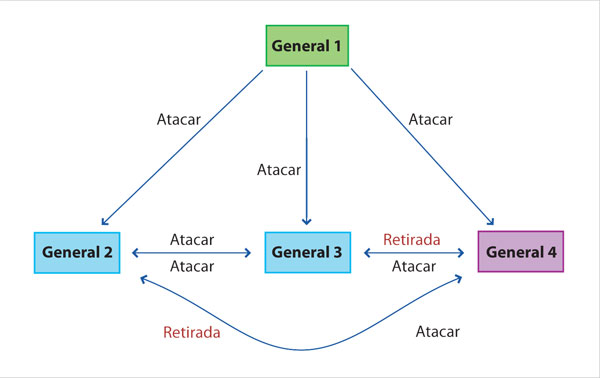
¿Cuántos generales se requieren al menos para lograr consenso en la decisión si hubiera tres generales traidores, es decir si t = 3? Se requieren mínimo "3t + 1" o lo que es lo mismo: 3 × 3 + 1 = 10 generales. Y, en este caso con tres traidores, ¿cuántos mensajes se tienen que enviar? Se tienen que realizar t + 1 "rondas" de mensajes. En la figura 2 se muestra la primera ronda, que intuitivamente significa, por ejemplo para el caso del general 2: "el general 1 (el supremo) me ordena…", pero una segunda ronda obliga al general 2 a decir "el general 3 me ha dicho que el general 1 ordenó…" y así para todos la segunda ronda involucra repetir lo que otro de los generales dice: "el general 3 me ha dicho que el general 4 dice que el general 1 ordenó…", y así sucesivamente.