Arcadio resolvió el problema en sólo dos minutos. Sin embargo, ¿qué tan bueno es su algoritmo? Si el algoritmo va a ser usado una sola vez, es difícil predecir qué tan bueno es su método de solución. ¿Servirá para resolver situaciones similares? ¿Arcadio podría enseñar el método a otras personas? Se puede pensar que el algoritmo va a ser empleado muchas veces. Obviamente, si Arcadio volviera a usar su algoritmo, no sería con la misma entrada que se dio en la tabla 3, puesto que ya conoce su solución. Entonces, considérese el conjunto de entradas posibles al problema, dado por:
Conjunto de entradas:
1] Una cantidad de dinero inicial: $ X.
2] Un conjunto de n regalos posibles: R = {R1, R2, …, Rn}.
3] Para cada regalo posible Ri de R, un precio en pesos, c(Ri), y un valor emocional, v(Ri).
Concepto
Un algoritmo tiene un conjunto de entradas válidas definido, de distintos tamaños. Cada vez que se ejecuta el algoritmo, es con un elemento de este conjunto.
Concepto
Cada elemento del conjunto de entradas tiene un tamaño. Mientras más grande sea la entrada, más recursos requerirá el algoritmo para producir una salida.
Curiosidades
Un camino que se bifurca una y otra vez indefinidamente, genera un número de posibilidades que crece exponencialmente. Éste es un tema recurrente en los libros de Jorge Luis Borges, al igual que los laberintos y los espacios de búsqueda inmensos.
Cada vez que Arcadio resuelve el problema, ejecuta su algoritmo con una entrada particular, con valores específicos de X, de R, de precios y valores. Por ejemplo, cuando Diana le sugirió otros dos regalos tuvo que ejecutar otra vez su algoritmo, ahora para n = 5, R = {pulsera, dije, aretes, CD, DVD}, con sus respectivos precios y valores (la X no cambia, sigue siendo igual a mil pesos).
Para evaluar la complejidad del algoritmo, en cuanto al tiempo que toma ejecutarlo, se debe considerar el tamaño de la entrada, pues no es lo mismo resolver el problema para tres regalos que para cinco o ¡para 50! Si el algoritmo de Arcadio funciona, deberá servir para resolver casos más complejos. Nótese que inclusive en los casos de tres regalos, el algoritmo debe funcionar para cualquier entrada, es decir, para cualquier conjunto de tres regalos, especificado cada uno por su precio y su valor emocional. Pero ¿qué sucede cuando se incrementa el número de regalos, o sea, el tamaño de la entrada n, a partir de n = 1?
Si sólo se considera un regalo (n = 1), se tendrían dos opciones: comprarlo o no. Si fueran dos objetos se obtendrían cuatro opciones: comprarlos ambos, no comprar ninguno y comprar alternadamente alguno de ellos y el otro no; el número de opciones resultante es el doble de las que había para un solo objeto. Cuando entran en escena los tres objetos tenemos, como se aprecia en la tabla 2, ocho opciones en total (el doble de las que teníamos para el número de objetos anterior). Mientras el número de objetos crezca de uno en uno, el número de opciones siempre se duplicará. Por ejemplo, si con cierto número de objetos se tienen x opciones y aparece un objeto más como un CD, el número de opciones será ahora 2x, ya que si originalmente había una opción: {pulsera no, dije sí, aretes no}, con el nuevo objeto se obtienen dos {pulsera no, dije sí, aretes no, CD no} y {pulsera no, dije sí, aretes no, CD sí}.
Inicialmente Arcadio tenía ocho posibilidades descritas en la tabla 2. Si añadiera el CD, el número de opciones sería 2 × 8 = 16; si incluyera el DVD, el número de opciones aumentaría a 2 × 16 = 32. Si añadiera otro regalo, 2 × 32 = 64, y uno más todavía, 2 × 64 = 128. En resumen, al ejecutar su algoritmo, Arcadio tiene que trazar una tabla cuyo número de filas crece conforme el número de regalos a considerar aumenta. A tres regalos corresponden ocho filas, y el tiempo para escribir en la tabla es de 8 × 10 segundos; con el CD son 16 filas y el tiempo es de16 × 10 segundos, y así sucesivamente.
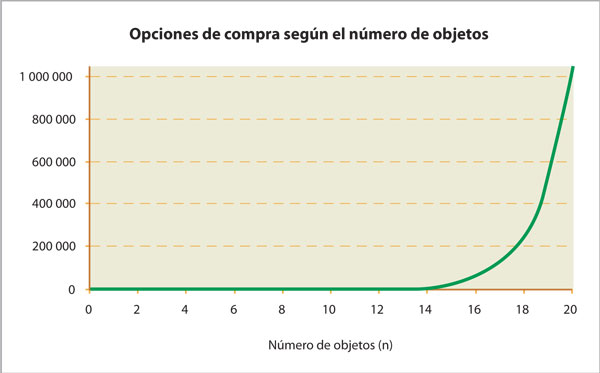
Si n representa el número de objetos, dependiendo del valor que adquiere, el número de posibilidades se comporta como se muestra en la tabla 4 y en la gráfica 1. Se observa que el número de posibilidades siempre es 2 elevado al número de objetos, es decir 2 n, lo que proviene de la multiplicación de 2 × 2 × 2… × 2, n veces, ya que cada vez que se añade un objeto se duplica el número de posibilidades. En términos de tiempo, Arcadio emplea 10 segundos para escribir en cada fila de su tabla, por consiguiente le tomará 10 × 2 n segundos llenar la tabla.
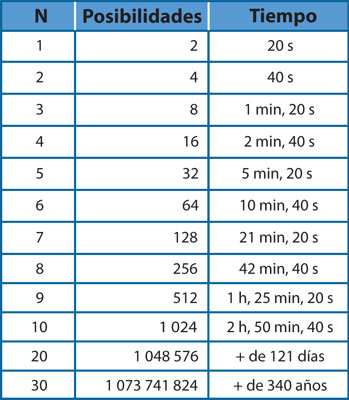
Basada en la fórmula anterior, la tabla 4 muestra el tiempo que emplearía Arcadio en escribir toda la tabla.
La n es la manera que se tiene para decir qué tan grande es la entrada al algoritmo. Al principio, Arcadio sólo consideró tres objetos de joyería; en ese momento n valía 3. Cuando entraron en escena los objetos restantes, producto de las sugerencias de Diana, Arcadio tenía n = 7 objetos.