Es posible diseñar circuitos que calculen cualquier función de conmutación usando compuertas. Por ejemplo, la función:
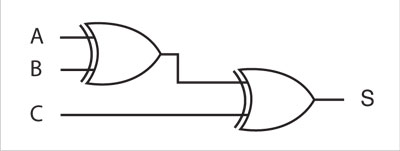
S(A, B, C) = A ⊕ B ⊕ C
es calculada por el circuito:
Por otra parte, la función:
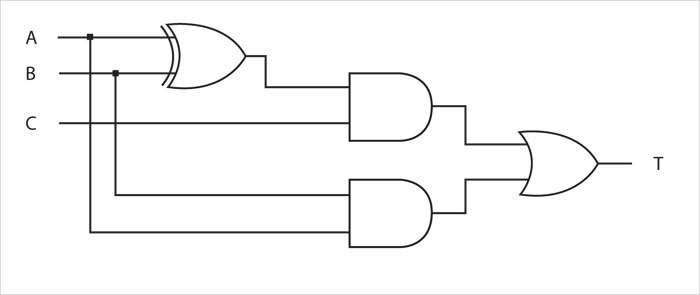
T(A, B, C) = C(A ⊕ B) + AB
se calcula con el circuito:
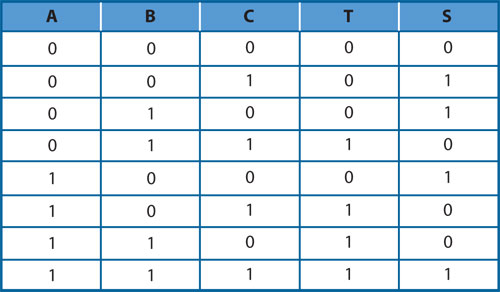
Estas dos funciones tienen, juntas, un significado peculiar. Para hacerlo evidente se debe recordar lo que se sabe acerca de la representación binaria posicional de los números: usando dos bits, el 0 se representa como 00, el 1 como 01, el 2 como 10 y el 3 como 11. Si se ponen las funciones en una tabla de verdad (tabla 3) y se toman en cuenta las columnas T y S juntas, como la expresión posicional binaria de un número, resulta que son la suma de los valores de las otras tres columnas: A, B y C. Es decir, si se presta atención a un renglón cualquiera de la tabla y se observa el número binario escrito en las columnas T y S, resulta ser el número de unos contenidos en ese mismo renglón en las columnas A, B y C. ¡Bien! Se ha construido la tabla de verdad de un circuito sumador. Normalmente, a la columna T se le denomina el acarreo de la suma, y a la columna S la suma propiamente dicha. En el sistema decimal, cuando se suman 8 y 5 el resultado es 13, es decir, tres unidades y una decena; en lenguaje coloquial "3 y llevamos 1"; ése 1 es el acarreo que significa que sumando los dígitos en una posición determinada se ha completado una unidad de la siguiente posición. En binario, si se suma 1 + 1 se obtiene 2, que en binario se escribe 10, es decir "0 y llevamos 1", o sea 0 unidades y una "biena".
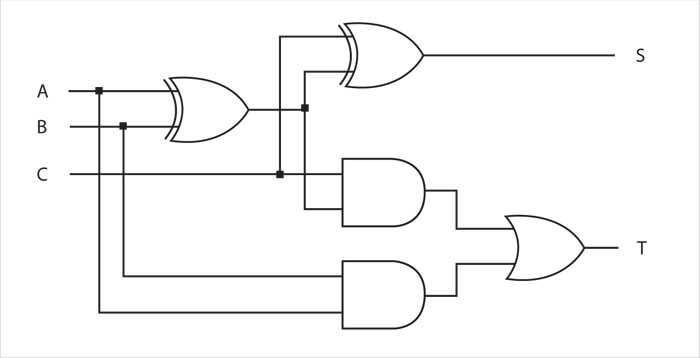
El circuito que se construyó se denomina sumador completo de un bit y se podría fabricar y ponerlo en una cajita cuyo interior se vería así:
Se denomina sumador de un bit y no de tres, porque realmente está sumando una sola posición de un par de números binarios, considerando que ya se tenía un acarreo previo, proveniente de la posición anterior, al que se designa C. Los bits que se suman son A y B. Así que ahora se puede ser más ambicioso y pensar en un sumador de números de ocho bits, lo que se vería así:
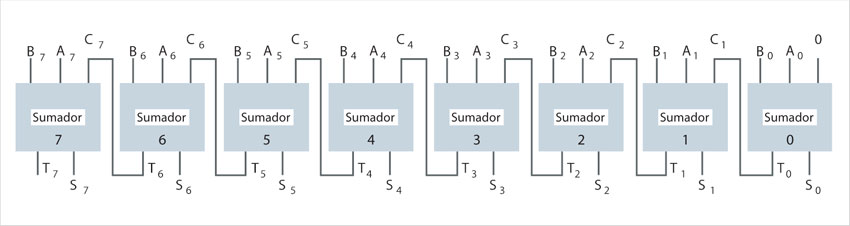
Los números que se suman son expresados en binario como: A7 A6 A5 A4 A3 A2 A1 A0 y B7 B6 B5 B4 B3 B2 B1 B0, el acarreo de entrada a la suma de A y B es, por supuesto, 0, por eso la línea de acarreo de entrada en el extremo derecho tiene escrito un 0.
Podría hacerse un sumador para números de cualquier tamaño, sólo hay que encadenar tantos sumadores de un bit como sea necesario. Del mismo modo, se puede pensar en hacer un circuito que multiplique o que haga cualquier operación que se ocurra. Éste es el principio de construcción de circuitos integrados: en cada chip se empacan unidades funcionales que permiten hacer algo particular. En este caso, se podría pensar en un primer chip con un sumador de un bit, luego intentar ser más ambiciosos y poner en un chip un sumador de ocho bits en cuyo interior se tendrían, de hecho, ocho sumadores de un bit; después podrían agregarse circuitos para hacer otras operaciones y añadir uno más para poder elegir cuál operación hacer.
Esto constituiría lo que se denomina una unidad aritmético-lógica (ALU, por sus siglas en inglés): el corazón de cualquier procesador central de una computadora o, en algún sentido, su cerebro.