Remedios le mostró a Arcadio algunas de las funciones de conmutación más simples: la conjunción ("y" o and en inglés) y la disyunción ("o" u or en inglés). Éstas son exactamente las mismas funciones que suelen usarse en el cálculo proposicional, como se puede ver en el tema de abstracción. Si se añade a este par de funciones una más, como la negación (el "no", o not en inglés), se obtiene un conjunto con el que es posible construir cualquier otra función de conmutación.
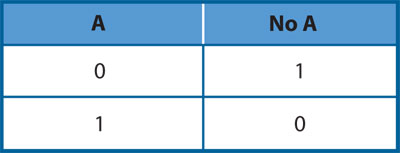
La negación es aún más simple que la disyunción o la conjunción: recibe un único argumento y entrega el complemento binario del mismo como resultado. En la siguiente tabla de verdad se muestra la negación.
Conviene aclarar algunas cosas a propósito de esta manera de representar funciones usando una tabla de verdad. Probablemente, el lector está acostumbrado a representar funciones mediante lo que se denomina una regla de correspondencia: una expresión algebraica que dice cómo calcular al valor que adquiere la variable dependiente, dado el valor de la independiente; algo del estilo de f(x) = 2x + 4, si se da un valor para la variable independiente, x = 3, entonces la regla dice qué valor de la variable dependiente le corresponde: f(3) = 2 × 3 + 4 = 10. Pero hay que recordar el sentido original del concepto de función: una relación que vincula a cada elemento de un conjunto (dominio) con uno y sólo uno de otro (contradominio). La regla de correspondencia es particularmente útil en el caso de las funciones en las que el dominio es infinito, porque de manera sintética permite definir qué elemento del contradominio le corresponde a ¡todos y cada uno de los elementos del dominio infinito! En el caso de las funciones de conmutación, sin embargo, la situación es bastante más sencilla, el dominio es finito; se puede hacer una lista de todos sus elementos y, por tanto, una tabla —a la que se denomina tabla de verdad—, en la que se especifique qué elemento del contradominio le toca a cada quien. Por supuesto, también se podría usar una regla de correspondencia (y se hará posteriormente).
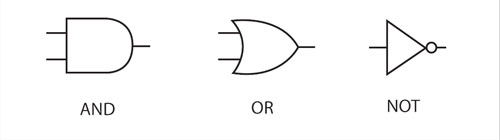
Las tres funciones elementales mencionadas: disyunción, conjunción y negación, constituyen una base (por cierto, no la única) sobre la que se puede construir cualquier otra función de conmutación y, por tanto, cualquier computadora. Debido a esto, los ingenieros suelen usar símbolos especiales para denotarlas al diseñar circuitos.
Es entonces importante poder expresar cualquier función de conmutación en términos de AND, OR y NOT. En adelante, se usará el símbolo "+" para denotar el OR o disyunción; el AND o conjunción se de-notará sin usar un símbolo particular, simplemente poniendo juntas las variables que intervienen en la operación: por ejemplo, AB denota la conjunción de A y B, variables booleanas. El NOT o negación se denotará poniendo una barra sobre la variable que se niega. Por ejemplo, la expresión:
f(A, B) = AB + AB
corresponde a una función cuya tabla de verdad es la tabla 2. Se muestra el cálculo de las variables negadas (columnas 4 y 5) y el de los términos parciales (columnas 6 y 7) para facilitar el de la función en la tercera columna:
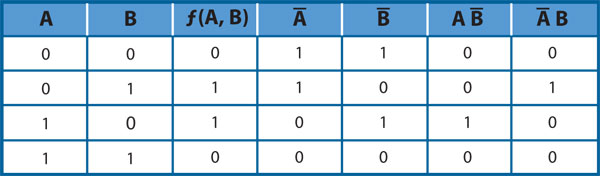
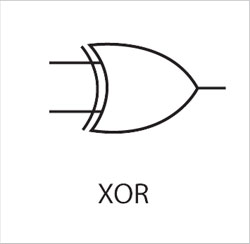
Esta función es también muy simple y bastante útil. Se le suele llamar disyunción exclusiva (XOR, en inglés). Es muy similar a la disyunción común, salvo que no es verdadera cuando ambos argumentos son verdaderos (de allí que se la llame exclusiva: si la disyunción es "A o B", la disyunción exclusiva es "A o B pero no ambos"). Si se piensa en interruptores, el XOR puede ser calculado por un interruptor de los llamados "de escalera": cuando ambos interruptores, el que está al pie de la escalera y el que está arriba, se encuentran en la misma posición, entonces el foco está apagado; si alguno de ellos cambia de posición, el foco se enciende.
La disyunción exclusiva es tan útil por sí misma que suele usarse el operador "⊕" para representarla en las expresiones de funciones de conmutación, y los diseñadores de circuitos también poseen un símbolo para ella:
A los símbolos usados para denotar las funciones AND, OR, NOT y XOR en los circuitos de electrónica digital se les denomina compuertas lógicas.