En efecto, en la lógica proposicional o equivalentemente, en el álgebra de las funciones de conmutación, no se pueden hacer deducciones muy complejas. Por ejemplo, las siguientes afirmaciones:
• Las plantas verdes tienen clorofila.
• El cilantro es una planta verde.
• Entonces, el cilantro tiene clorofila.
En la lógica proposicional quedarían representadas por:
• P
• Q
• P => Q
Lo que no sirve de mucho porque no dice nada acerca de la validez de la última expresión a partir de las anteriores. La lógica proposicional considera independientes las afirmaciones anteriores, no puede expresar la tercera como conclusión de las anteriores, se necesita mayor complejidad en la abstracción para expresar propiedades que son satisfechas por ciertos objetos y además para decir cuántos de esos objetos las satisfacen.
En la lógica de primer orden, si se usa el símbolo V(x) para decir que x es una planta verde y C(x) para decir que x tiene clorofila, entonces se tiene:
• Para toda x, si V(x) entonces C(x).
• V (cilantro).
• Por lo tanto, C (cilantro).
Ahora puede verse la tercera afirmación como una deducción derivada de las dos primeras; es posible apreciar mayores detalles de las afirmaciones al considerarlas constituidas elementos menores como la cuantificación de "para toda" y los predicados V y C, que ahora son cosas susceptibles de ser evaluadas como falsas o verdaderas dependiendo de a quién le son aplicadas.
Ésta es una herramienta esencial, no sólo en computación, porque toda la matemática está basada en ella. La lógica de primer orden se utiliza para demostrar cualquier afirmación hecha en matemáticas, es su herramienta deductiva. Es, por cierto, una abstracción muy poderosa; en la última representación del ejemplo ya no importa realmente qué significa V o C o cilantro. Muy bien se podría decir que cilantro es el nombre de un amigo, que V(x) significa que x es un holgazán y que C(x) significa que x reprueba el curso y la deducción seguiría siendo válida. Más aún, podrían ser cosas que ni siquiera tengan sentido: cilantro es el nombre de un habitante del planeta Hoth, V(x) significa que es un "trupiciante" y C(x) significa "algerobio". La primera afirmación dice que todo trupiciante es algerobio, no se sabe qué significa eso pero no importa, el caso es que si luego nos dicen que cilantro es un trupiciante entonces se deduce que es algerobio. La validez de la afirmación proviene de la forma que tiene, de lo que se escribe, no de lo que significa lo que se escribe (si es que significa algo).
Con base en esta herramienta es posible demostrar la corrección de los algoritmos y verificar, en casos particulares, cuándo terminan y cuál es el estado en el que lo hacen.
Verificación de corrección de programas
El siguiente es un algoritmo para calcular la media aritmética (promedio) de una lista de números. Con lista[i] se denota el i-ésimo número de la lista.

A manera de ejemplo, se analizará este algoritmo. Lo que se pretende calcular es tan simple que intuitivamente se sabe que es correcto; el código del algoritmo expresa exactamente el proceso que se realiza para calcular el promedio manualmente, a saber, calcular:

No hay motivos para pensar que el algoritmo no es correcto. Pero, en general, los algoritmos que suelen utilizarse en muchas situaciones reales son bastante más complejos; asegurarse de que entregan el resultado correcto siempre puede ser muy difícil. Cabría preguntarse, ¿por qué se sabe que el algoritmo es correcto?, ¿cómo asegurarse de que realmente lleva a cabo el cálculo para el que fue pensado?
El algoritmo supuestamente calcula el promedio de los números guardados en una lista. En la línea 2 se asigna un cero a la variable suma, se puede decir entonces que cuando se llega por primera vez a la línea 3, la variable suma contiene la suma de los primeros cero elementos de la lista. La siguiente vez que se llega a la línea 3, la variable i tiene un 1 y la variable suma contiene lo que tenía (0), más el valor guardado en la posición 1 de la lista; es posible afirmar que la variable suma contiene entonces la suma del primer elemento de la lista. En la siguiente llegada a la línea 3, i vale 2 y la variable suma contiene la suma de los primeros dos elementos de la lista y así sucesivamente. Siempre que se llega a la línea 3, la variable suma contiene la suma de los primeros i elementos de la lista. En notación de predicados se diría:
a] Si P = {0, ..., tamaño(lista)} entonces, para toda i P,
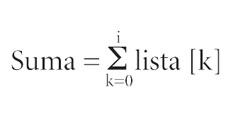
luego de la i-ésima repetición del ciclo de las líneas 3 a 5.
También se tiene que:
b] Al llegar a la línea 6, i = tamaño(lista).
Así que fácilmente se deduce que:
c] Al llegar a la línea 6, suma contiene la suma de todos los elementos de la lista. Es decir:
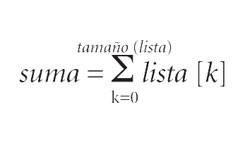
Finalmente, en la línea 6 se calcula el resultado que es, como se ve en el código, el contenido de la variable suma dividido por el tamaño de la lista. De donde se deduce:
d] El resultado final del algoritmo es:
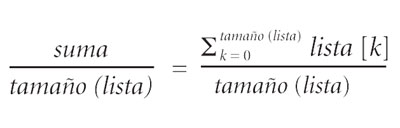
Lo que coincide con la definición de promedio, por lo que ahora se puede tener la seguridad de que el algoritmo es correcto.
A una expresión como la del predicado A se le denomina invariante de ciclo, es un predicado verdadero siempre que se ejecuta un ciclo (no necesariamente durante la ejecución del mismo). Usando la lógica de primer orden y el invariante de ciclo fue posible demostrar que el algoritmo es correcto. Éste es un procedimiento sólido, y todo buen programador recurre a él con frecuencia, al menos implícitamente.
Razonar para resolver problemas-acertijos
Con la lógica de primer orden como herramienta deductiva es posible resolver problemas que resultan insolubles a simple vista. Considérese el ejemplo de la siguiente historia: luego de una desigual batalla en la que resultó vencedor, Harald, hijo de Hafni, se entregó al sueño, agotado por la lucha. Sleipnir, hechicero enemigo de Harald, aprovechó la condición del héroe para secuestrarlo y así, en medio de su profundo sueño, éste fue llevado por medio de artes mágicas a un amplio salón en el castillo de Sleipnir. Así permaneció Harald, dormido, ignorante de su situación, durante varios días. Cuando despertó se halló encerrado en el enorme salón sin otra compañía que una lechuza y un oso, con la habilidad de hablar el lenguaje humano, y que en realidad eran otras víctimas de Sleipnir. Se oyó de pronto la estentórea voz de Sleipnir retumbando en el salón: "Sólo podrás salir si adivinas qué día de la semana es hoy". El mago confiaba en mantener atrapado al héroe a sabiendas de que éste había perdido la noción del tiempo por haber estado dormido varios días. Acto seguido anunció: "Seré benévolo contigo, Harald, hijo de Hafni. El oso que te acompaña está obligado a decir sólo mentiras los lunes, martes y miércoles; la lechuza no puede sino mentir los jueves, viernes y sábados; el resto de los días ambos sólo dicen verdades. Demuestra que tu mente es tan poderosa como tu espada." El oso le dijo entonces a Harald: "Ayer fue uno de los días en que me toca mentir"; la lechuza declaró por su parte: "¡Qué coincidencia! Ayer también fue uno de los días en que debo mentir". Harald se sentó abatido en el suelo; luego de unos momentos de reflexión, se levantó y gritó: "Sleipnir, permíteme liberar del hechizo a estos desgraciados junto conmigo". Al cabo de unos minutos se oyó la voz del hechicero: "Harald, hijo de Hafni, he de reconocer tanto la valía de tu generoso corazón como tu soberbia, ¿te crees capaz de vencerme? No seré yo quien te reproche tu fracaso, sino los infelices que te acompañan. Te concederé su libertad y la ruptura del hechizo que pesa sobre ellos si logras saber qué día de la semana es hoy. Mi honor queda empeñado en ello." Acto seguido Harald gritó: "Hoy es el día consagrado al poder de Thor,2 que su martillo te aplaste si no nos liberas en este jueves." Cayeron las puertas del recinto, Harald pudo sentir el viento de las montañas otra vez y en sus futuras aventuras le acompañaron siempre Alder y Elder, dos robustos guerreros que alguna vez fueron un oso y una lechuza.
¿Cómo logró Harald saber el día de la semana?
1] Supóngase que L es la lechuza. Los días en que la lechuza miente son M(L) = {ju, vi, sa}. Luego, los días en que dice sólo la verdad son V(L) = {do, lu, ma, mi}.
>2] Si O es el oso. Los días en que miente son M(O) = {lu, ma, mi}. Los días en que sólo dice la verdad son V(O) = {ju, vi, sa, do}.
3] Se ve claramente que no hay días en que la lechuza y el oso mientan simultáneamente, en notación de conjuntos: M(L) ∩ M(O) = Ø.
4] Así que para cualquier día x, uno de los dos animales necesariamente dice la verdad.
5] Con A(x) se denotará el día anterior a x. Según el oso A(hoy) € M(O). Según la lechuza A(hoy) € M(L). Pero esto significaría que A(hoy) € M(L) ∩ M(O). Esto, por lo expresado en el inciso 3, no puede ser; entonces alguno de los dos miente (el inciso 4 impide que ambos mientan).
6] Supóngase que quien miente es el oso. Eso significa que hoy es uno de los días en que le toca mentir a él y a la lechuza no. Como la lechuza no miente entonces lo que dice es verdad, ayer fue uno de sus días de mentir. Eso significaría que A(hoy) = sa y entonces hoy sería domingo. Pero si fuera domingo el oso tampoco estaría mintiendo (los domingos nadie miente) y eso contradice lo que se está suponiendo.
7] Supóngase entonces que es la lechuza quien miente. Entonces hoy es uno de los días en que le toca mentir a la lechuza y al oso no. Éste hoy dice la verdad y ayer le tocó mentir, eso significa que A(hoy) = mi y, por tanto, hoy es jueves, como bien dedujo Harald, lo que confirma que es día que la lechuza miente.